算数はいつでも3ステップで:学習のデザイン03
行動経済学は一区切りして、学習のデザインシリーズを再開します。
いま、子どもの勉強で中学校入試の勉強を少し見ているので、国算理社について、自分なりの整理の仕方を紹介します。まずは算数からです。
1. 計算間違いはほんの一部
算数が得意というと、計算がすぐにできる人を想像しがちですが、計算だけで取れる点数は全体の中で少しだけです。
多くの問題は文章問題になります。文章から「この問題では何を答えればよいか?」や「何の数字が使えるか」といった読解力が欠かせません。なので国語のスキルも大事です。(もし英語で文章が出されたら多くの日本人は答えらえないはずです)

算数の点数が良くないと感じている子どもは、実は計算ではなく、文章の読み解きをとばしていたり、何を答えればよいかを見失っている場合が多くあります。
ここで、デザインの力を借りましょう。やみくもに問題を解くのではなく、一度整理してみて、子どもは「何につまづいているのか?」を理解することによって、成長のキッカケをつかめるはずです。
2. 思考の型を持つ
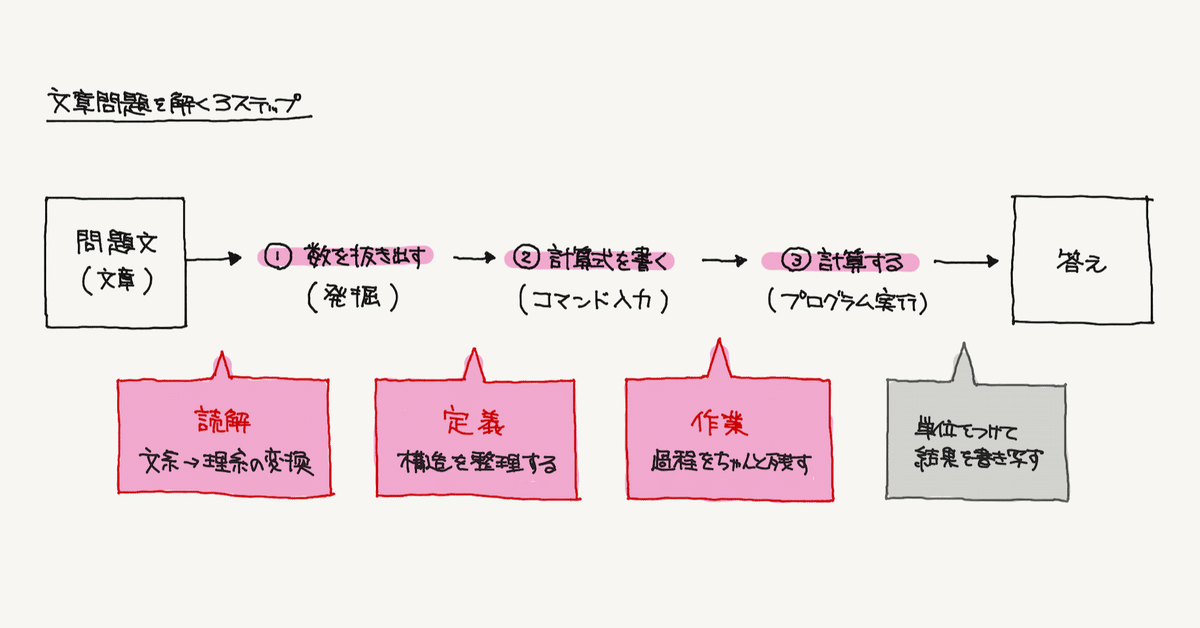
すべての算数の文章問題を、3つに構造分解してみましょう。
① 数を抜き出す(発掘)
② 計算式を書く(コマンド入力)
③ 計算する(プログラム実行)
大人であれば、プログラミングやエクセルの計算式のステップをイメージしてもらうと分かりやすいかと思います。算数の文章問題でもこれと同じような思考が求められます。
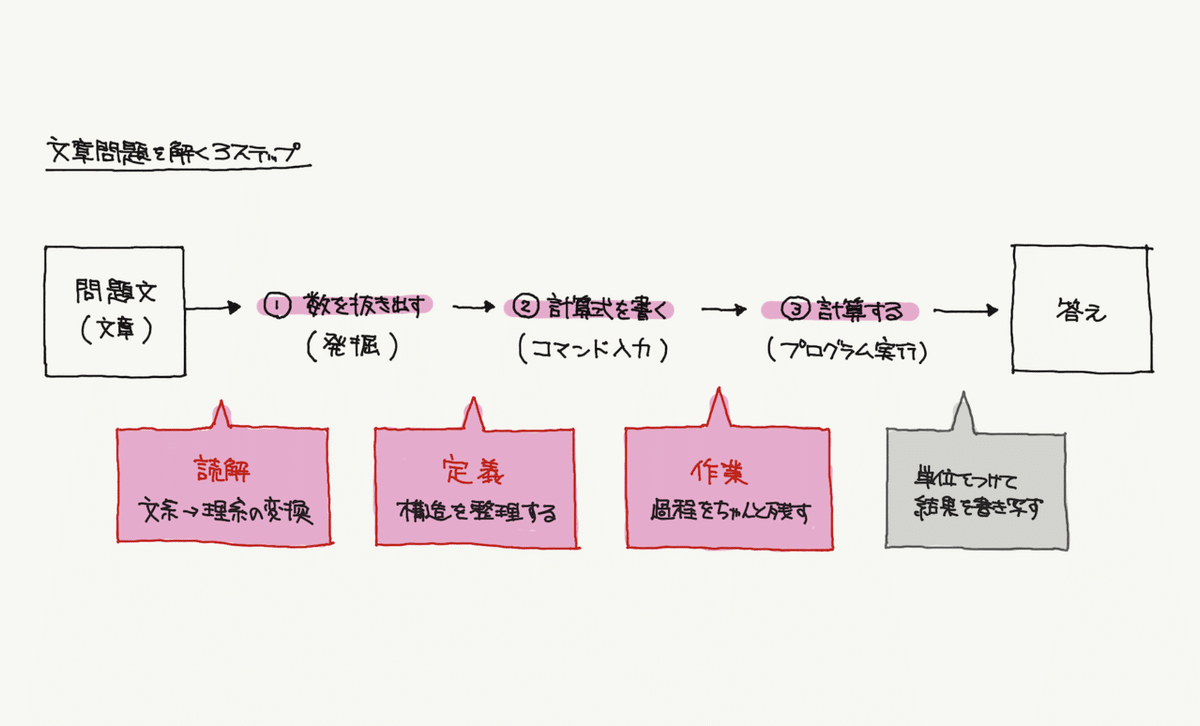
まずはじめ①で、答えを出すために、文章から必要な数字を発掘します。ここは国語(文系)から算数(理系)の変換作業です。計算は得意なのに文章問題で間違えてしまう人は、ここが注力点(伸びしろ)です。
次に②で、抜き取った数字をもとに計算式を設定します。ここを一足飛びで計算してしまうと「何の計算してたんだっけ?」と分からなくなってしまうので、式を定義してから計算することはとても大事です。
最後に③で計算します。この段階まできたら、機械的に答えを出す作業に注力します。(もちろん計算式の過程は丁寧に書くように)
この①②③のステップで解いていけば、どこで間違えたか、どこで分からなくなったかが明らかになるので、リバースエンジニアリングの発想で原因を特定して、「分からない」を「分かった!」変えていけます。
3. A4一枚で教える
子どもの算数のノートは、計算式でびっしりです。後からノートだけを見返しても、本人もほとんど何のことかわからないはずです。(子どものノートを勝手に拝借、ごめん。)
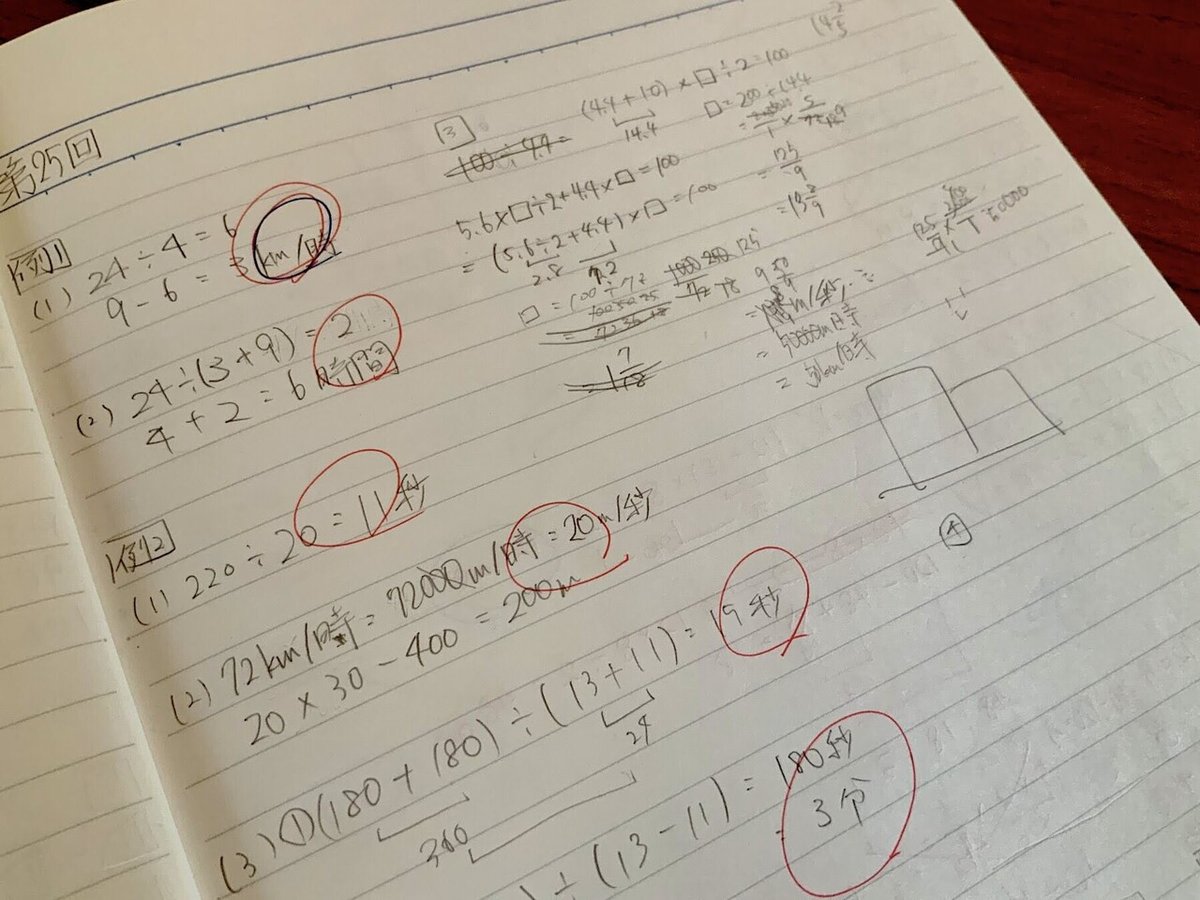
ここでデザインの出番です。上にあげた3ステップを定着させるために、書くノートのフォーマットをそろえるのがよいかと考えます。

左ページが計算問題、右ページが答えを書くスペースです。見開き一枚で一問、ちょっとぜいたくな使い方ですが、このくらいスッキリさせた方が、頭の中が整理できるはずです。
右ページは大きく①②③で分けます。どんな簡単な問題でもこの3点を書くことによって、解き方が分からなくなった場合でも、ステップをたどって解法を思い出すことができるようになります。
手書きの例は、つるかめ算(僕が小学生のときは知らなかった)ですが、まず、文章から①でこのようなことが読み取れます。
・30円切手と70円切手があり、合計が3160円
・合計100枚だけど、それぞれ何枚かが分からない
・つるかめ算の公式に当てはめればよいと気づく
それを①→②につなげます。式ができたら、あとは③で淡々と計算します。

これによって、段階を踏んで答えにたどり着けます。間違えていたら、計算の③なのか、それよりも②の式自体か、①の抜き取りの整理かを分析することができます。
4. 文章→図表の変換
①②③のなかで最も大切なのは、②の計算式を設定することです。
コンピューターであれば、②さえ正しくできれば答えは出せます。大人になったら③は自分でやらなくなります。(でも自分でやればできることが大事)
対して①は、読解力や想像力が求められ、方法も1つではありません。①の書き方は問題によって書き方は変わってきます。箇条書きもあれば、線分図や表にして整理する方法もあります。ポイントは文章(文系)→図表(理系)への変換ですが、これは社会人になっても求められることで、大人でも苦手な人はたくさんいます。僕を含めて。

学校の勉強が社会に出て何の役に立つのか?と言われたら、僕は上にあげたような「文章と図表の行き来ができるようになる」と答えます。僕自身は仕事でこれが役に立ったことはたくさんあります。
算数が難しいと感じていたら、一度ブレイクダウンして、1つずつ積み上げて何が壁かを見つけましょう。ノートの書き方や、教え方の構造を変えることで、もっと算数が面白くなるはずです。
・・・・・
こんな感じでデザインを活用してみてください。次はたぶん理科です。
いいなと思ったら応援しよう!

