ファイナンス機械学習:機械学習を使ったアセットアロケーション 練習問題 固有値行列をスケール変換する
前問のNアセットのPnL行列の共分散行列をスペクトル分解し、スケール変更によるポートフォリオの重みの変化を比較する。
共分散行列を$${{\bf V}}$$、$${{\bf V}}$$の固有ベクトル行列を$${{\bf W}}$$、固有値を対角に並べたものを$${{\bf Lambda}}$$とすれば、
$${{\bf V W}={\bf W \Lambda}}$$である。
eVal,eVec=np.linalg.eigh(cov)
eVal=np.diag(eVal)$${{\bf \epsilon}}$$を、[0,1]の標準正規分布に従う乱数ベクトルとする。
これを使い、$${{\bf Lambda}}$$を以下のようにリスケーリングする。
$${\tilde{\Lambda}_{n,n}=\displaystyle{ N\times \frac{ \epsilon_n \Lambda_{n,n}}{\sum^{N}_{n=1}\epsilon_n}}}$$
これを共分散として用いてクラスタリングを行った結果を、元の共分散行列を使ったクラスタリングと比較したのが下の図である。

また、$${\tilde{{\bf V}}}$$を使い、HRP,CLA,IVPでポートフォリオの重みを計算した。其々を元の共分散$${{\bf V}}$$での重みと比較したのが下のグラフである。
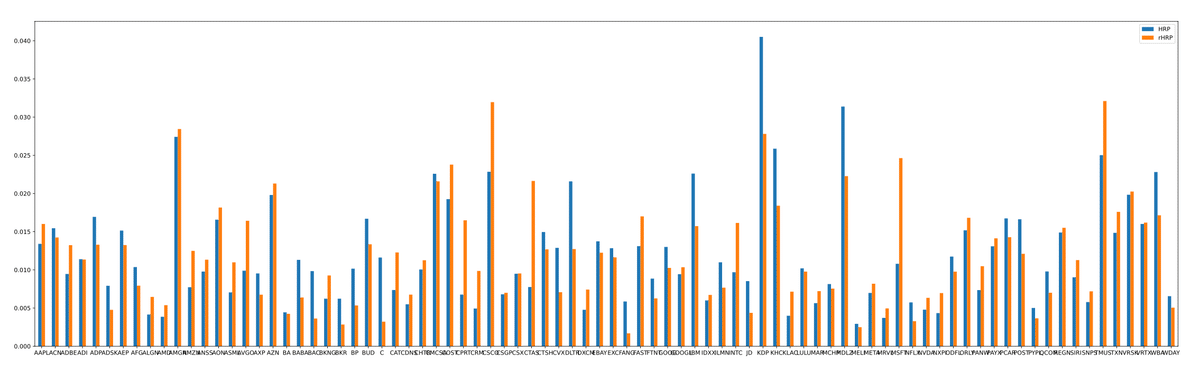


リスケールした影響が大きく出ているのは、CLAである。
