アセットマネージャーのためのファイナンス機械学習：ポートフォリオの構築　人工データを使った実験

Dean4rmEdinburgh

数値実験で、NCOアルゴリズムとマコーウィッツ法の性能を比較する。
ポートフォリオの構築に不可欠な最小分散ポートフォリオと最大シャープレシオポートフォリオを扱う。
　コードスニペット7.6は、NCOアルゴリズムを用い、o変数muがNoneの場合は最小分散ポートフォリオ、muがNone出ない場合は最大シャープレシオのポートフォリオ$${{\bf \omega}}$$を返す。

def optPort_nco(cov, mu=None, maxNumClusters=None):
    cov = pd.DataFrame(cov)
    if mu is not None:
        mu = pd.Series(mu[:,0])
    
    corr1 = MP.cov2corr(cov)
    corr1, clstrs, _ = NC.clusterKMeansBase(corr1, maxNumClusters, n_init=10)
    
    #wIntra = pd.DataFrame(0, index=cov.index, columns=clstrs.keys())
    wIntra= pd.DataFrame(0, index=cov.index, columns=clstrs.keys(),dtype='float64')
    for i in clstrs:
        cov_ = cov.loc[clstrs[i], clstrs[i]].values
        if mu is None:
            mu_ = None
        else: 
            mu_ = mu.loc[clstrs[i]].values.reshape(-1,1)
        wIntra.loc[clstrs[i], i] =MP.optPort(cov_,mu_).flatten()    
    
    cov_= wIntra.T.dot(np.dot(cov, wIntra)) 
    mu_ = (None if mu is None else wIntra.T.dot(mu))
    wInter= pd.Series(MP.optPort(cov_,mu_).flatten(), index=cov_.index)    
    
    
    nco = wIntra.mul(wInter, axis=1).sum(axis=1).values.reshape(-1,1)
    return nco

さらに、スニペット7.7で、クラスタ内相関が0.5のサイズ5のブロック10個からなる50銘柄のポートフォリオを模した人工データのランダムなリターンの平均値ベクトルと共分散行列を生成する。

nBlocks, bSize, bCorr = 10, 5, .5
np.random.seed(0)
mu0, cov0 = MP.formTrueMatrix(nBlocks, bSize, bCorr)

これを元に、ノイズ除去の章で実装されたsimCovMuで雑音を入れ、NCO使用と無使用でマーコウィッツ解のサンプルを1000作成して、雑音を混入していない元データでの解との二乗誤差をとる。

def simCovMu(mu0,cov0,nObs,shrink=False):
    x=np.random.multivariate_normal(mu0.flatten(),cov0,size=nObs)
    mu1=x.mean(axis=0).reshape(-1,1)
    if shrink:cov1=LedoitWolf().fit(x).covariance_
    else:cov1=np.cov(x,rowvar=0)
    return mu1,cov1
def PortExp(mu0, cov0, nObs=1000, nSims=1000, shrink=False, minVarPortf = True):
    np.random.seed(0)
    w1 = pd.DataFrame(0, index=range(0, nSims), 
                  columns=range(0, cov0.shape[0]),dtype='float64')
    w1_d = pd.DataFrame(0, index=range(0, nSims), 
                    columns=range(0, cov0.shape[0]),dtype='float64')
    for i in range(0, nSims):
        mu1, cov1 = MP.simCovMu(mu0, cov0, nObs, shrink=shrink)
        if minVarPortf:
             mu1 = None
    
        w1.loc[i] = MP.optPort(cov1, mu1).flatten() 
        w1_d.loc[i] = optPort_nco(cov1, mu1, int(cov1.shape[0]/2)).flatten() 
    return w1, w1_d

最小分散ポートフォリオ

minVarPortf=True

w1, w1_d=PortExp(mu0=mu0,cov0=cov0,minVarPortf=minVarPortf)
w0 = MP.optPort(cov0, None if minVarPortf else mu0)
w0 = np.repeat(w0.T, w1.shape[0], axis=0) #true allocation

print('minVar Markowitz RMSE: ',
      round(np.mean((w1-w0).values.flatten()**2)**.5,4))
print('minVar NCO RMSE:',
      round(np.mean((w1_d-w0).values.flatten()**2)**.5,4))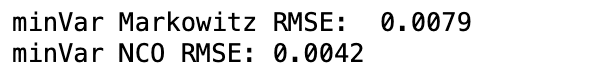
最小分散ポートフォリオ

最大シャープレシオポートフォリオ

minVarPortf=False

w1, w1_d=PortExp(mu0=mu0, cov0=cov0,minVarPortf = minVarPortf)
w0 = MP.optPort(cov0, None if minVarPortf else mu0)
w0 = np.repeat(w0.T, w1.shape[0], axis=0) 

print('Market Markowitz RMSE: ',
      round(np.mean((w1-w0).values.flatten()**2)**.5,4))
print('Market NCO RMSE:',
      round(np.mean((w1_d-w0).values.flatten()**2)**.5,4))
最大シャープレシオポートフォリオ

この記事が気に入ったらサポートをしてみませんか？