ファイナンス機械学習:人工データを使ったバックテスト 練習問題 ショートポジションの最適戦略
価格100で開始したショートポジションを90の利益確定と105の損切りを条件にしまう最適戦略を、OU過程を使い、閾値レベルの妥当性と、それに合うパラメータを探す。
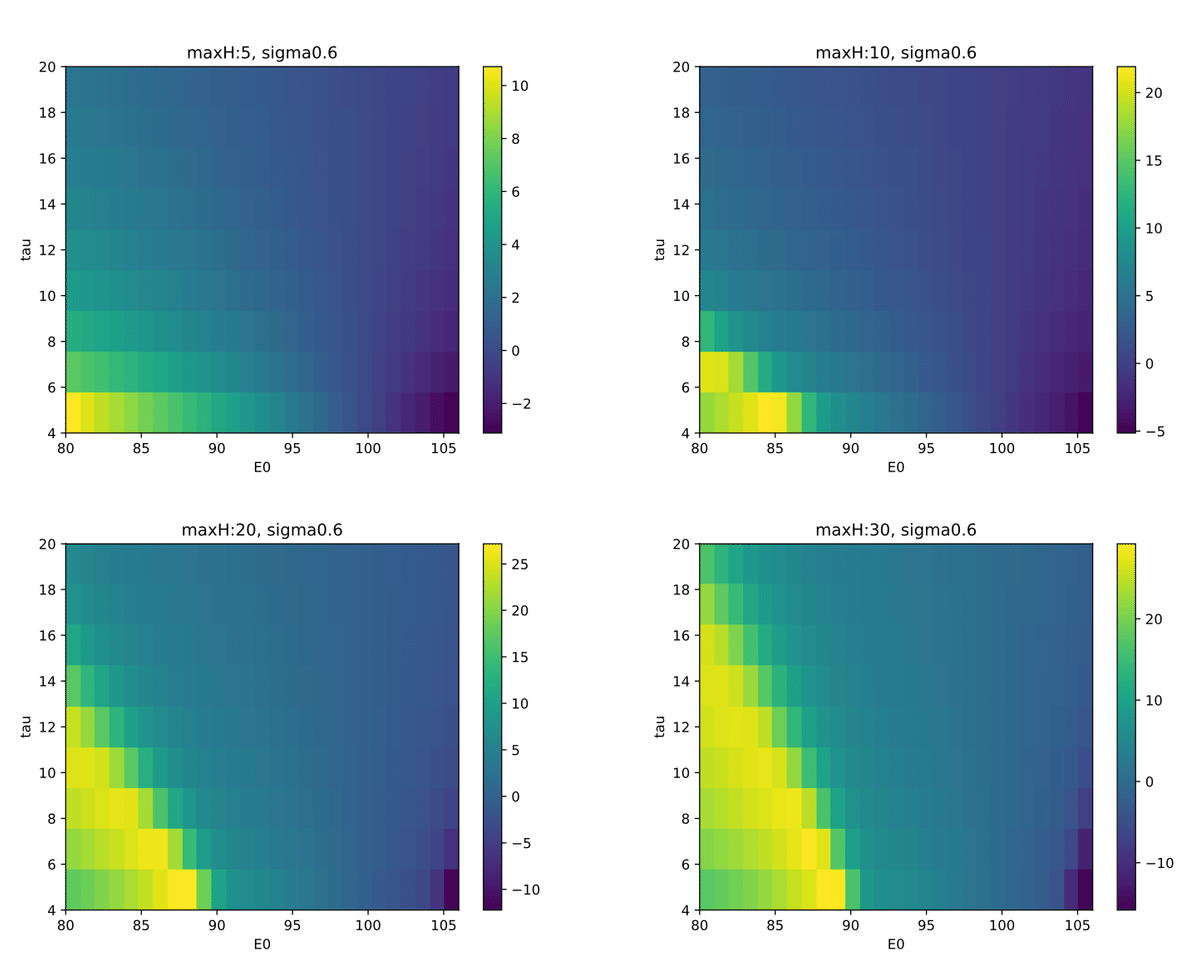
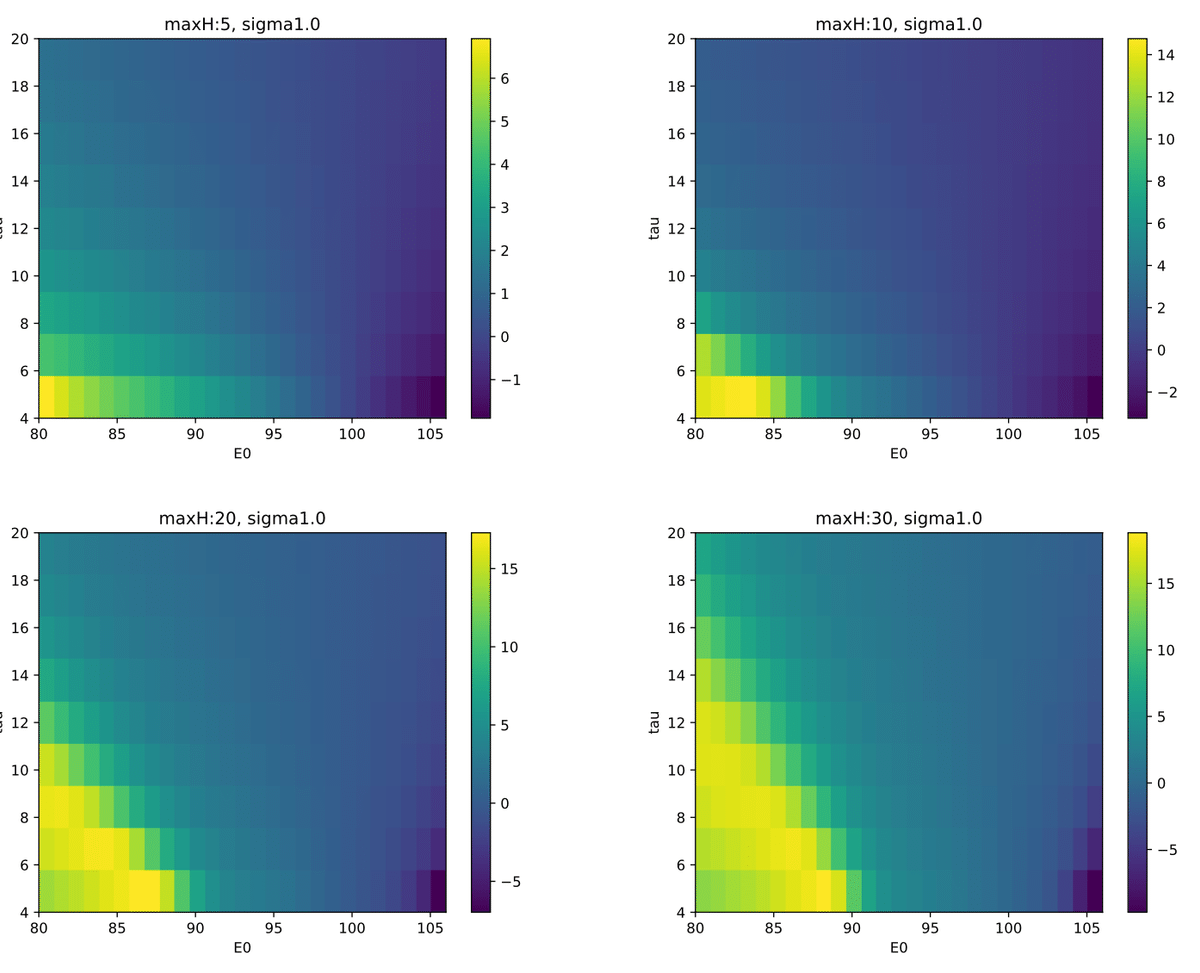
長期期待リターン$${E_0}$$と半減期の$${\tau}$$を、最長保持期間$${maxH}$$と分散$${\sigma}$$を変えて、シャープレシオをヒートマップで示した。
E0=np.linspace(80,106,27)
tau=np.linspace(4,20,9)
sig=[0.6,0.8,1.0,1.2,1.6]
p0=100
T=1
maxH=[5,10,20,30]
rPT=105-p0
rSLm=-(90-p0) # this is rPT for short position
columns=['E0','tau','mean','std','sr']
for mh in maxH:
for sigma in sig:
output=strt_ET(E0,tau,sigma,paths=1e5, maxH=mh,dt=dt,rPT=rPT,rSLm=rSLm,p0=p0)
df=pd.DataFrame(output,columns=columns)
sr=df.sort_values(by=['E0','tau'])['sr']
sr=-1*sr.to_numpy().reshape(len(E0),-1) #Note this is short position
plt.imshow(sr.T,cmap='viridis', extent=(E0[0], E0[-1], tau[0], tau[-1]),
aspect='auto',interpolation='nearest',origin='lower')
plt.title(f'maxH:{mh}, sigma{sigma}')
plt.xlabel('E0')
plt.ylabel('tau')
plt.colorbar()
filename=f'./ShortP_maxH{mh}_sig{sigma}.pdf'
plt.savefig(filename)
plt.show()
plt.clf()