ファイナンス機械学習：分数次差分をとった特徴量　練習問題　E-mini S&P500先物ドルバー

Dean4rmEdinburgh

E-mini S&P500の先物ドルバーに、いくつかの$${d\in[0,2]}$$を用いて固定ウィンドウ法分数次差分を適用する。

import Labels as labels
import Bars as bars
from datetime import datetime

SP_data = pd.read_csv('SP.csv')
SP_data = SP_data[SP_data['volume'] > 0]
SP_data['datetime'] = SP_data['date'] + "/" + SP_data['time']
SP_data['datetime'] = SP_data['datetime'].apply(lambda dt: datetime.strptime(dt, '%m/%d/%Y/%H:%M:%S.%f'))
#SP_data=SP_data[SP_data['datetime'] >= datetime(2009, 1, 1)]

SP_data.index=SP_data['datetime']
SP_data.drop(['date','time'],axis=1, inplace=True)
SP_data.drop(['datetime'],axis=1, inplace=True)
SP_data.volume=SP_data.groupby(SP_data.index).volume.sum()
SP_data = SP_data[~SP_data.index.duplicated(keep='first')]

dv=500_000
Dbar=bars.getDollarBars(SP_data,dv)
close = Dbar['Close'].to_frame()

FW = Dbar['Close'].to_frame()
FWD=FW
dd=[0.01, 0.02, 0.04, 0.08, 0.1, 
    0.12, 0.14, 0.16, 0.18, 0.2,
    0.4, 0.8 , 1.6, 1.8]
print('Original Price DATA)
printADF(FW)
for d in dd:
    FFD=fracDiff_FFD(series= FW, d= d, thres= 1e-5)
    print(str(round(d,2)))
    printADF(FFD)
    FFD=FFD.rename(columns = {'Close':str(round(d,2))})
    FWD=FWD.join(FFD,how='left')
ドルバー時系列の分数次差分　d＜0.4

オリジナル時系列は、p値ADF統計量とも単位根を持つ非定常時系列でだと判定されているが、$${d=0.18}$$で、定常になり、これより大きいdでの差分は過剰差分でメモリーが失われていると言える。
$${d=0.18}$$で差分された時系列とオリジナル時系列をグラフ化すると、以下のようになる。

fig, ax1 = plt.subplots()

ax2 = ax1.twinx()
ax1.plot(FWD['Close'],'r-')
ax2.plot(FWD['0.18'],'b-',alpha=0.4)

ax1.set_xlabel('X data')
ax1.set_ylabel('Price', color='r')
ax2.set_ylabel('d=.18', color='b')

plt.show()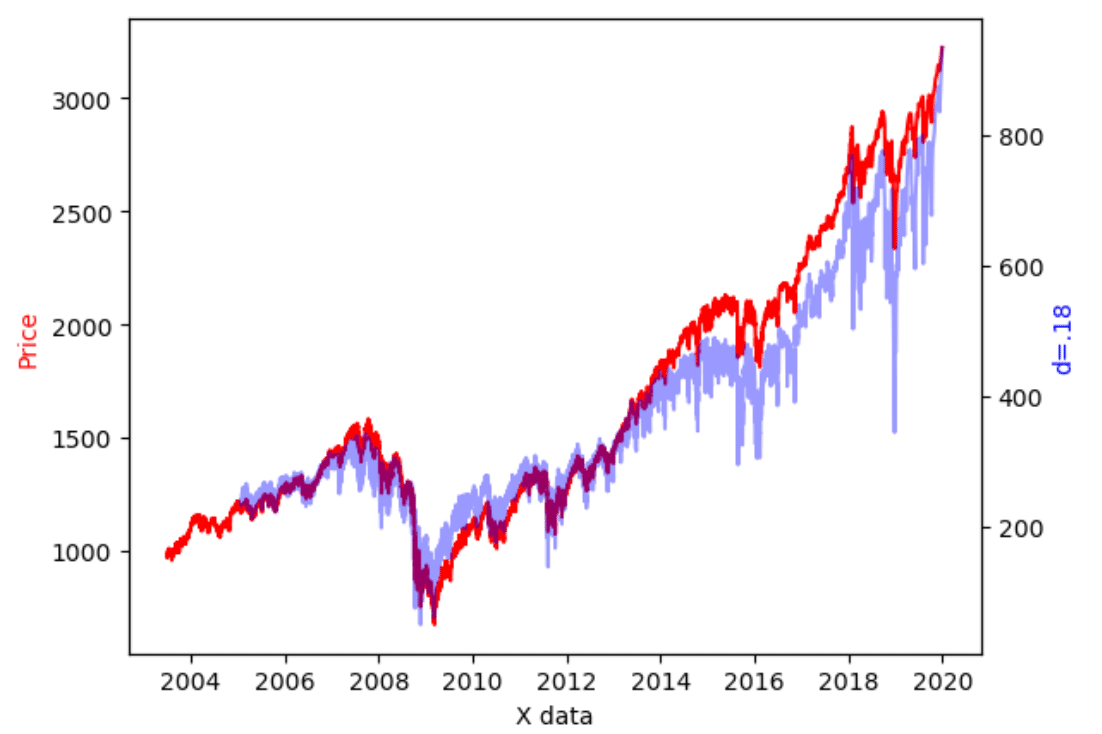
固定幅ウィンドウ法d=0.18で定常化した時系列と、
オリジナルのドルバー時系列


いいなと思ったら応援しよう！