ファイナンス機械学習:分数次差分をとった特徴量 練習問題 IIDガウス過程時系列と正弦関数時系列
メモリーのない定常時系列であるIIDガウス過程の時系列を作成し、ADF検定を行う。
def printADF(process):
adf, p_value, _, _, _ = adfuller(process, maxlag=1,regression='c', autolag=None)
print(f'ADF statistics: {adf}')
print(f'p-value: {p_value}')
# generate 10000 IID random numbers
num = 10000
mu = 0
sd = 1
GX = np.random.normal(mu, sd, nsample)
printADF(GX)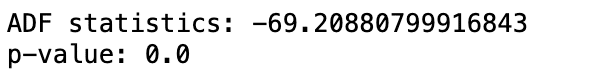
検定量は負であり、p値も低いので、ADFの帰無仮説単位根の存在は棄却され、この時系列は定常である。
累積時系列を作成し、同様にADF検定を行う。累積時系列は一次の和分である。

検定量はマイナスではあるが、p値は5%より高く、時系列は単位根を持ち、非定常である。
この累積時系列の差分を2回取り、ADF検定を行う。

一次和分の時系列を2回差分し、過度差分させたADF検定は定常である。
正弦関数に従う時系列を作成し、ADF検定を行う。
num = 10000
x = np.linspace(0, 10, num)
sinX = pd.Series(np.sin(2.*x+0.5))
printADF(sinX)
p値より、定常時系列である。
この時系列を$${+1}$$シフトし、累計を取った時系列は、メモリーを持つ非定常時系列である。ADF検定からそれを確かめる。

ADF値は正でp値は1となり、明らかに非定常である。
これに拡大ウィンドウ法分数次差分を、$${\tau=1e-2}$$として適用し、ADF検定のp値が5%を下回る最小のd値を求める。
d,outEx=plotMinFFD(sinXsf_cumsum,False,thres=.01)
fdmin=fracDiff(pd.DataFrame(sinXsf_cumsum),d,thres=.01)
printADF(fdmin)
plt.plot(fdmin)
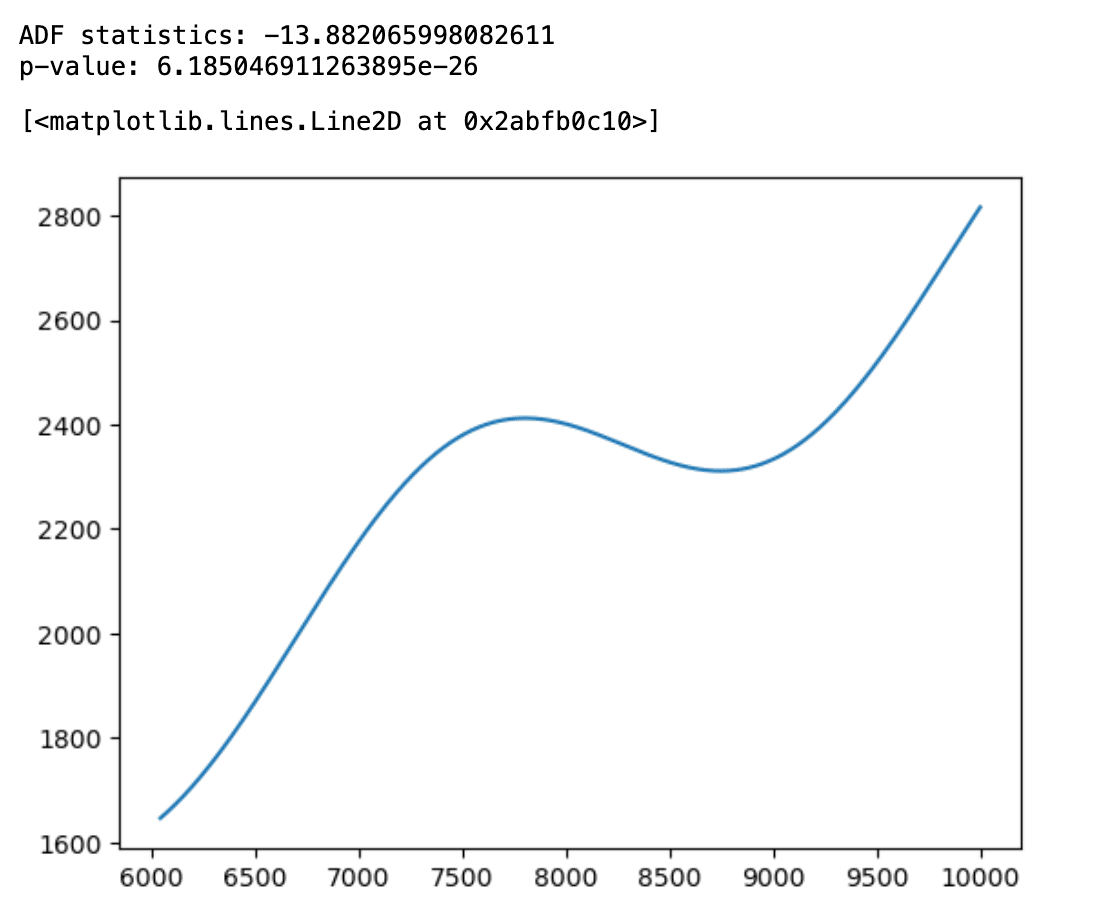
同じ時系列を固定ウィンドウ法分数次差分で、最小dを求めADF検定を行う。
d,outFx=plotMinFFD(sinXsf_cumsum,True,thres=1e-5)
fdmin=fracDiff_FFD(pd.DataFrame(sinXsf_cumsum),d,thres=1e-5)
printADF(fdmin)
plt.plot(fdmin)

