ファイナンス機械学習：分数次差分をとった特徴量　練習問題　E-mini S&P ドルバーの対数価格累積分数次差分へのトリプルバー　決定木

Dean4rmEdinburgh

前記事でトリプルバーを適用して得たラベルを、決定木バギング分類器を使ってフィッティングするが、ここでは、sklearn.ensembleのbaggingClassifierの引数の一つmax_samplesに、ラベルの平均独自性を重みとして与える。
　max_samplesは、渡される値が整数$${n}$$であった場合は、特徴量$${X}$$から、$${n}$$個のサンプルをブートストラップ法でサンプリングし、値が実数$${r}$$であれば、$${X.shape[0]\time r}$$個のサンプルをブートストラップ法でサンプリングする。決定木のパラメータ、テストデータ、トレーニングデータは前記事と同じとする。

nCoEvent=wg.getNumCoEvents(dfEvents.index,t1,dfEvents.index)
TW=wg.getSampleTW(t1,nCoEvent,dfEvents.index)

from sklearn.ensemble import BaggingClassifier


skl_bag = BaggingClassifier(estimator = tree,
                                n_estimators = n_estimate, # the number of trees as a estimate
                                max_samples = TW.mean(), #if you put max_sample = 1.0, pls mentally get ready to wait
                                max_features = 1.0,
                                bootstrap = True, #must always be True
                                bootstrap_features=False,
                                oob_score = True, # You will need to have bootstrap = True
                                warm_start = False,
                                n_jobs = 1, # For parallel computering, -1 means use all
                                random_state = random_state, #seed figure
                                verbose = 0)

# Fit and score
skl_bag.fit(X_train, y_train)
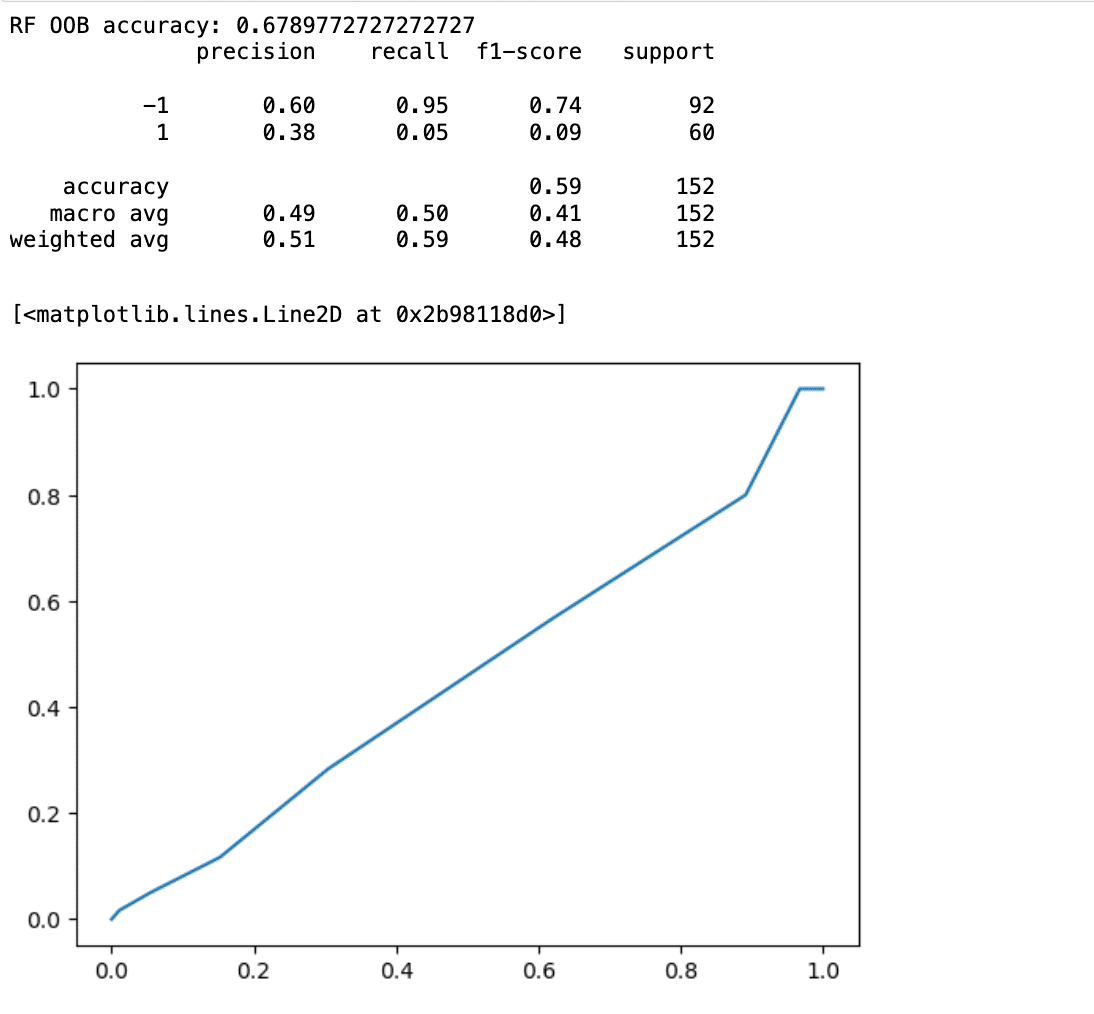
print(f'RF OOB accuracy: {skl_bag.oob_score_}')
y_sklpred = skl_bag.predict(X_test)
y_sklprob = skl_bag.predict_proba(X_test)[:,1] 

print(classification_report(y_true=y_test, y_pred=y_sklpred))

fpr, tpr, thresholds = roc_curve(y_test, y_sklprob)
    
roc_auc = auc(fpr, tpr)
plt.plot(fpr,tpr,label=' ROC area = %0.2f' %(roc_auc))
max_sample=TW.mean()を与えた決定木バギング分類器の評価とROC曲線


この記事が気に入ったらサポートをしてみませんか？