ファイナンス機械学習：分数次差分　拡大ウィンドウ法

Dean4rmEdinburgh

時系列への分数差分の実装を行う。

拡大ウィンドウ

　時系列$${\{X_t\},t=1,\dots T}$$の$${d}$$次の分数差分をとることは、$${\displaystyle{w_k = -w_{k-1}\frac{d-k+1}{k}}}$$より、各時点$${k}$$にウエイト級数を与えることになり、計算量とデータ量を考えれば不可能である。
　よって、各時点でのウエイト級数は、各時点で持っている異なるメモリー量を表しているとし、$${I}$$時点での相対ウエイト損失$${\displaystyle{\lambda_I=\frac{\sum^T_{j=T-I}|w_j|}{\sum^{T-1}_{i=0}|w_i|}}}$$を定める。損失許容値$${\tau \in [0,1]}$$を用いて、$${\lambda^*_I \le \tau}$$かつ、$${\lambda^*_{I+1} > \tau}$$の、相対ウエイト損失が許容値を超えている時系列の初めの$${\{X_t\},t=1,\dots I^*}$$を示す$${I^*}$$を与える。
$${d=1}$$の時、$${w_k=\{1,-1,0 \dots 0\}}$$であるから、$${\lambda_{I}=0, I > T-1}$$。よって、$${\tau=0.01}$$とすれば、$${\lambda_{T-1}=1/2 > \tau}$$ 、$${I^*=T-2}$$から、最初の$${\tilde{T}_1}$$が捨てられる。
　ウエイト損失許容度を入れた拡大ウィンドウによる時系列の分数次差分は、スニペット5.2で与えられている。

def fracDiff(series, d, thres=.01):
    '''
    Fractional differentiation with increasing width window
    Note 1: For thres=1, nothing is skipped
    Note 2: d can be any positive fractional, not necessarily bounded [0,1]
    
    '''
    
    w=getWeights(d, series.shape[0])
    w_=np.cumsum(abs(w))
    w_/=w_[-1]
    skip = w_[w_>thres].shape[0]
    df={}
    for name in series.columns:
        seriesF,df_=series[[name]].ffill().dropna(),pd.Series(dtype='float64')
        for iloc in range(skip,seriesF.shape[0]):
            loc=seriesF.index[iloc]
            if not np.isfinite(series.loc[loc,name]): continue
            df_[loc]=np.dot(w[-(iloc+1):,:].T,seriesF.loc[:loc])[0,0]
        df[name]=df_.copy(deep=True)
    df=pd.concat(df,axis=1)
    return df

このコードを使い、E-miniS&P先物トレードのドルバーについて、$d=0.4,\tau=1$と$d=0.4,\tau=1e-4$の比較を以下のグラフに示す。

import Labels as labels
import Bars as bars
from datetime import datetime
SP_data = pd.read_csv('SP.csv')
SP_data = SP_data[SP_data['volume'] > 0]
SP_data['datetime'] = SP_data['date'] + "/" + SP_data['time']
SP_data['datetime'] = SP_data['datetime'].apply(lambda dt: datetime.strptime(dt, '%m/%d/%Y/%H:%M:%S.%f'))
#SP_data=SP_data[SP_data['datetime'] >= datetime(2009, 1, 1)]

SP_data.index=SP_data['datetime']
SP_data.drop(['date','time'],axis=1, inplace=True)
SP_data.drop(['datetime'],axis=1, inplace=True)
SP_data.volume=SP_data.groupby(SP_data.index).volume.sum()
SP_data = SP_data[~SP_data.index.duplicated(keep='first')]
close = Dbar['Close'].to_frame()

fd0=fracDiff(series = close, d =.4, thres=1).dropna()
fd1=fracDiff(series = close, d =.4, thres=1e-4).dropna()

EXWind=pd.DataFrame(index=close.index).assign(
    Close=close,
    tau_1=fd0).dropna()
EXWind[['tau_1', 'Close']].plot(secondary_y='Close',figsize=(10,8))

EXWind1=pd.DataFrame(index=close.index).assign(
    Close=close,
    tau_1e_4=fd1).dropna()
EXWind1[['tau_1e_4', 'Close']].plot(secondary_y='Close',figsize=(10,8))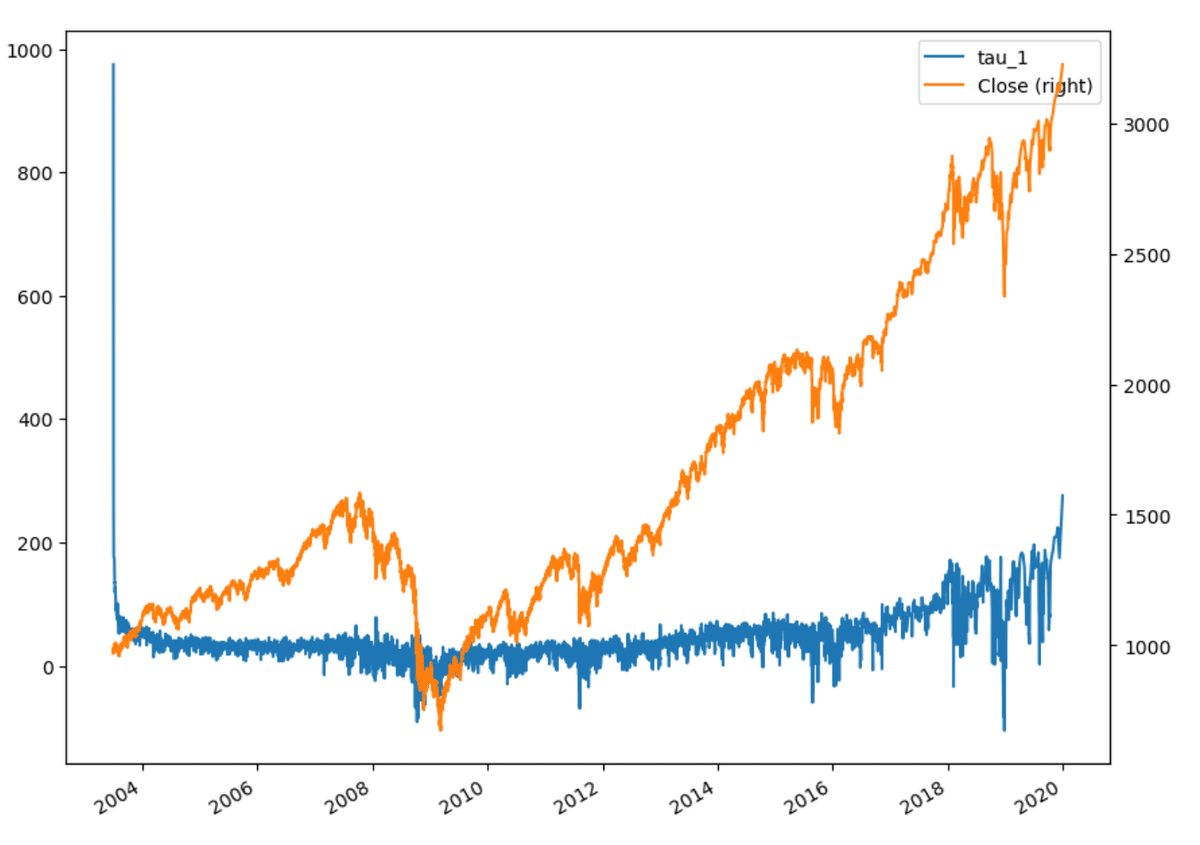
E-mini S&P 500 先物ドルバー　
d=0.4、相対ウエイト損失許容量=1で拡大ウィンドウ法での分数次差分
E-mini S&P 500 先物ドルバー　
d=0.4、相対ウエイト損失許容量=1e-4で拡大ウィンドウ法での分数次差分

この記事が気に入ったらサポートをしてみませんか？