ファイナンス機械学習：標本の重み付け　練習問題　平均独自性の低いデータセットにランダムフォレストを適合させる

Dean4rmEdinburgh

E-mini S&P500の先物のティックデータより、ドルバーを作成し、これにトリプルバリアを適用して、バリアに接触した時間のt1行列を導出した。
　このラベルの平均独自性を計算し、その平均値を取ってみる。

avgUniq=mpSampleTW(t1=TPevents['t1'],numCoEvents=NumConc,period=TPevents.index)
avgUniq.sum()/len(avgUniq)
平均独自性のサンプル平均

これは、$${\displaystyle{\frac{\sum_{i=1}^I \bar{u}_i}{I}}<<1}$$を満たす。
　このデータに、ランダムフォレストを適合さた、アウトオブバッグの平均正解率は以下のように計算される。

TPlabels=labels.getBinsTUML(TPevents,price,t1)
TPlabels = TPlabels[~(TPlabels['bin'] == 0)]

short=5
long=20
Xy=(pd.DataFrame()
            .assign(price=Dbar['Close'])
            .assign(ewm=Dbar['Close'].ewm(short).mean()-Dbar['Close'].ewm(long).mean())
            .assign(s_skew=Dbar['Close'].rolling(short).skew())
            .assign(s_kurt=Dbar['Close'].rolling(short).kurt())
            .assign(l_skew=Dbar['Close'].rolling(long).skew())
            .assign(l_kurt=Dbar['Close'].rolling(long).kurt())
            .assign(rtn=DbarRtn)
            .assign(vol=DailyVol)
            .assign(label=TPlabels['bin'])
         ).dropna()

Xy = Xy[~Xy.index.duplicated(keep='first')]

X= Xy.drop('label',axis=1).values
y = Xy['label'].values.astype(int)

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, shuffle=False)

n_estimators, max_depth, c_random_state = 32, 8, 1
rf = RandomForestClassifier(max_depth = max_depth, 
                            n_estimators = n_estimators,
                            criterion = 'entropy',
                            #bootstrap=True,
                            #max_samples = av_uniqueness_by_coevent['tW'].mean()
                            oob_score = True,
                            class_weight = None, #This will be covered later
                            random_state = c_random_state)

rf.fit(X_train, y_train)
print(f'RF OOB accuracy: {rf.oob_score_}')

ランダムフォレストの引数のbootstrapとmax_samplesは、今はオフにし、アウトオブバッグoob_scoreはTrueにする。
　このアウトオブバッグのスコアは、

であった。
　シャッフルをオフにしたk-分割交差検証の平均正解率は、

from sklearn.model_selection import cross_val_score
accuracies = cross_val_score(rf, X_train, y_train, cv=5)
print(f'RF mean cross validation accuracy: {accuracies.mean()}')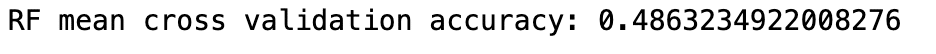

明らかにアウトオブバッグの正解率の方が高い。これは、標本が同時独立分布であるという間違った前提のもとで、サンプリングを行った結果、冗長性の高いサンプリングが行われたからである。

この記事が気に入ったらサポートをしてみませんか？