
【Pythonで統計モデル】SEM3:パス解析(逐次モデル)
はじめに
株式会社GA technologiesの白土です。
この記事はPythonで統計モデル(SEM編)の続きであり、構造方程式モデリング(SEM:Structural Equation Modeling)をPythonでどこまで実行できるかを調査・確認することを目的にしています。
現在私が所属しているデータサイエンスチーム(以下DSチーム)では、構造方程式モデリングの勉強会を行っています。
これまではChief Data Scientistである福中さんがこのシリーズを更新していましたが、今後はメンバーも含めてリレー形式で更新していく予定です。
興味のある方は、ぜひご一読後にAISC Magazineのフォローをお願いします!
シリーズとしてはDSチーム全体での取り組みではありますが、私自身は本格的に統計学の勉強を始めたのも最近であり、SEMに関しても初学者です。
もし誤りや補足、あるいは感想などありましたらいただけると大変助かります!
また、この記事では東京図書から出版されている共分散構造分析[R編]―構造方程式モデリング―で取り上げられていた事例を、Pythonを使って再現していきます。分析用データは東京図書のホームページからダウンロードできますので、興味のある方はぜひ試してみてください。
ちなみにGAtechnologiesにはスキルアップを目指すエンジニア向けの「テックチャージ」という制度があり、この書籍の購入に際しても会社に負担してもらいました。
環境
本記事の分析は、OS: MacOS 12.4、Python 3.9.12の環境下で行っています。また、必要なパッケージは以下となります。インストール済みの方は割愛してください。
# packageのインストール
pip install numpy pandas matplotlib japanize_matplotlib
pip install graphviz
pip install factor_analyzer
pip install semopyなおsemopyは構造方程式モデリング(SEM )を行うためのパッケージで、ドキュメントは以下にあります。
本記事ではここから重要な部分をいくつかピックアップしてご紹介します。網羅的な解説はしませんので、適宜、必要に応じてご参照ください。
パス解析・逐次モデル
今回はsemopyを用いて逐次モデルのパス解析を行います。パス解析とは「観測変数だけで構成される、複数の説明変数で複数の目的変数を説明する分析手法」です。そのためモデルは構造方程式のみで構成されています。
パス解析は大きく分けて逐次モデルと非逐次モデルの2種類に分類できます。逐次モデルは「単方向の矢印だけを辿って元に戻る変数が一つもないモデル」で、非逐次モデルは「単方向の矢印だけを辿って元の変数に戻ることができる変数が存在するモデル」です。また自由度(「分散共分散行列の対角要素を含む下三角行列の数」から「推定する母数」を引いた数)が0の逐次モデルは特に完全逐次モデルと呼ばれています。
例えば以下のような3つのモデルがあった際にモデル1とモデル3は逐次モデル、モデル2はx3→x4→x3と単方向の矢印を辿ることでx3に戻ることができるので非逐次モデルになります。

では実際にsemopyを用いて逐次モデルのパス解析を行っていきます。
パッケージとデータの読み込み
import pandas as pd
import numpy as np
from factor_analyzer.utils import covariance_to_correlation
import semopydata1 = pd.read_csv("dat/marriage.csv", encoding='shift_jis')今回使用するのは「結婚相手の条件データ」で、項目として「x1(学歴)」「x2(職業威信)」「x3(年収)」「x4(評価)」が含まれています。
print(data1.head())# 出力結果
x1 x2 x3 x4
0 2.40 33.64 1.115 0.75
1 2.96 41.37 1.545 2.09
2 3.08 45.00 1.666 2.59
3 3.53 49.70 1.815 2.19
4 2.25 43.97 1.854 1.72分析の実行
今回は「学歴」と「職業」が「年収」に、また「年収」と「職業」が「評価」に影響を与え、「学歴」と「職業」には互いに相関があることを想定し、以下のようなモデルを作成します。
model1 = """
x3 ~ x1 + x2
x4 ~ x2 + x3
x1 ~~ x2
x1 ~~ x1
x2 ~~ x2
"""semopyはlavaanと比較すると「よしな力」が劣っているところが幾らかあるようです。
例えばsemopyでは「外生的な潜在変数同士の共変関係」は自動で計算されますが、「外生的な観測変数同士の共変関係」は上記のように明示的に記載する必要がありました。
mod = semopy.Model(model1)
result = mod.fit(data=data2, obj='MLW')
ins = mod.inspect(std_est=True)
print(ins)分析結果を表示すると小数点第2位の精度でテキストと一致していることが確認できます。
またx1とx2の共変関係が求められており、外生変数であるx1とx2の分散の標準化解は1.0に固定されています。
# 出力結果
lval op rval Estimate Est. Std Std. Err z-value p-value
0 x3 ~ x1 0.683142 0.532283 0.075402 9.059985 0.000000e+00
1 x3 ~ x2 0.058144 0.323849 0.010548 5.512228 3.543197e-08
2 x4 ~ x2 0.022894 0.298112 0.005020 4.560656 5.099400e-06
3 x4 ~ x3 0.211090 0.493506 0.027959 7.549893 4.352074e-14
4 x1 ~~ x2 8.108391 0.698819 0.976816 8.300838 0.000000e+00
5 x1 ~~ x1 1.623167 1.000000 0.158405 10.246951 0.000000e+00
6 x2 ~~ x2 82.942571 1.000000 8.094366 10.246951 0.000000e+00
7 x3 ~~ x3 0.991572 0.370873 0.096768 10.246951 0.000000e+00
8 x4 ~~ x4 0.226404 0.462844 0.022095 10.246951 0.000000e+00続いてモデルの適合度指標を求めると以下のようになりました。
stats = semopy.calc_stats(mod)
print(stats.T)# 出力結果
Value
DoF 1.000000
DoF Baseline 6.000000
chi2 1.141680
chi2 p-value 0.285298
chi2 Baseline 511.970821
CFI 0.999720
GFI 0.997770
AGFI 0.986620
NFI 0.997770
TLI 0.998320
RMSEA 0.026036
AIC 17.989127
BIC 48.113095
LogLik 0.005437Rでも出力した結果の一部を抜粋したものが以下になります。
lavaan 0.6.15 ended normally after 1 iteration
Estimator ML
Optimization method NLMINB
Number of model parameters 6
Model Test User Model:
Test statistic 1.142
Degrees of freedom 1
P-value (Chi-square) 0.285
User Model versus Baseline Model:
Comparative Fit Index (CFI) 1.000
Tucker-Lewis Index (TLI) 0.998
Root Mean Square Error of Approximation:
RMSEA 0.026自由度などの基本情報と、CFIやTFIなどの適合度指標が小数点第2位まで一致しているのを確認できました。
なお、SRMRについてはsemopyでは出力するためのメソッドは準備されていないため、別途自分で計算する必要があります。詳しくはPythonで統計モデル(SEM編)第1回の記事をご覧ください。
パス図の描画
続いてsemplotを使ってパス図を書いていきます。
semopy.semplot(model, "graph.png", std_ests=True, plot_covs=True)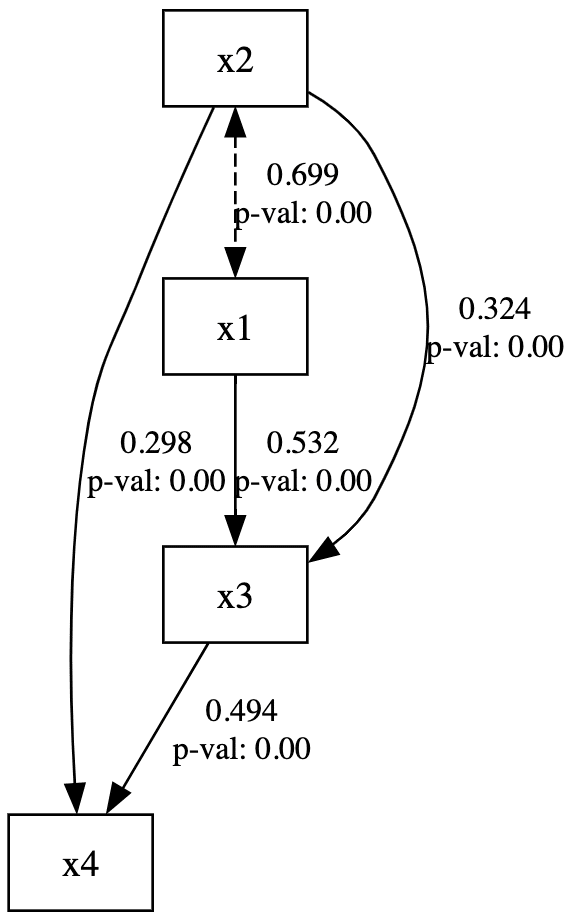
パラメータ「std_ests」は「標準化するかどうか」を、「plot_covs」は「共変関係のパスを表示するかどうか」を指定しています。その他のsemplotのパラメータに関しては以下で確認できます。
中には「engine」や「latshape」のようなパス図の見た目を調整できそうな変数もありますが、単純に指定しただけでは私の環境だと上手く動作しませんでした。
semopy.semplot(model, "graph.png", std_ests=True, plot_covs=True, engine="circo")
semplotはGraphvizというツールのラッパーなので、慣れている方はGraphvizの形式で修正をすればある程度見た目を整えることができるようです。
g = semopy.semplot(model, "graph.png", std_ests=True, plot_covs=True)
print(g.source)# 出力結果
digraph G {
overlap=scale splines=true
edge [fontsize=12]
node [fillcolor="#cae6df" shape=circle style=filled]
node [shape=box style=""]
x4 [label=x4]
x1 [label=x1]
x2 [label=x2]
x3 [label=x3]
x1 -> x3 [label="0.532\np-val: 0.00"]
x2 -> x3 [label="0.324\np-val: 0.00"]
x2 -> x4 [label="0.298\np-val: 0.00"]
x3 -> x4 [label="0.494\np-val: 0.00"]
x2 -> x1 [label="0.699\np-val: 0.00" dir=both style=dashed]
}import graphviz
graphviz.Source("""
digraph G {
overlap=scale splines=true
edge [fontsize=12]
node [fillcolor="#cae6df" shape=circle style=filled]
node [shape=box style=""]
x4 [label=評価]
x1 [label=学歴]
x2 [label=職業]
x3 [label=年収]
x1 -> x3 [label="0.53"]
x2 -> x3 [label="0.32"]
x2 -> x4 [label="0.30"]
x3 -> x4 [label="0.49"]
x1 -> x2 [label="0.70" dir=both style=dashed]
pad=0.2
rank = same { x1, x2}
rank = same { x3, x4}
}
""")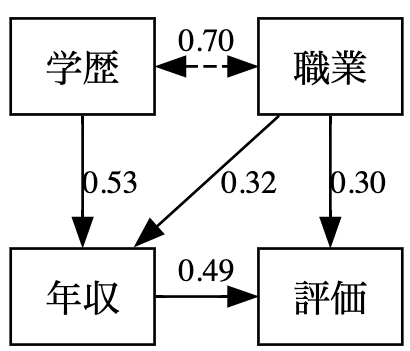
しかしいずれにしても限界がありそうなので、semplotのパス図はあくまで簡易的な確認をするためのものとして割り切って、レポートや論文に使用する際には改めて他のツールでパス図を作成した方が良いのかな、と思いました。
最後に
今回の分析を実行する中で、lavaanとの違いは以下だったのではないかと思います。
・「外生的な観測変数同士の共変関係は明示的に記載する必要がある」などの「よしな力」の不足。
・パス図が簡易的なものしか作成できない。
ですが気をつけてさえいれば分析の結果自体には影響がないので、semopyでも逐次モデルのパス解析は問題なく行えると考えて良いと思います。
今後の流れ
次回は非逐次モデルのパス解析について三田さんに更新していただく予定です。
興味のある方は、ぜひAISC Magazineのフォローをお願いします!
