
機械学習:R言語(Tidymodels)チュートリアルの和訳④
Build a model
tidymodelsを使用して統計モデルを作成するにはどうすればよいでしょうか?この記事では、その手順を詳しく説明します。モデル作成のためのデータから始め、parsnipパッケージを使用して異なるエンジンでモデルを指定しトレーニングする方法を学び、これらの関数がなぜこのように設計されているのかを理解します。
library(tidymodels) # for the parsnip package, along with the rest of tidymodels
library(readr) # for importing data
library(broom.mixed) # for converting bayesian models to tidy tibbles
library(dotwhisker) # for visualizing regression resultsConstable (1993) のデータを使用して、3つの異なる給餌方法が時間の経過に伴い海胆のサイズにどのように影響するかを探ってみましょう。実験の開始時の海胆の初期サイズは、給餌されることでどれだけ大きく成長するかに影響する可能性があります。
まず、海胆データをRに読み込みます。これは、CSVデータが置かれているURLを readr::read_csv() に提供することで行います(“https://tidymodels.org/start/models/urchins.csv”):
urchins <-Data were assembled for a tutorial
at https://www.flutterbys.com.au/stats/tut/tut7.5a.html
read_csv("https://tidymodels.org/start/models/urchins.csv") %>%
Change the names to be a little more verbose
setNames(c("food_regime", "initial_volume", "width")) %>%
Factors are very helpful for modeling, so we convert one column
mutate(food_regime = factor(food_regime, levels = c("Initial", "Low", "High")))urchins
#> # A tibble: 72 × 3
#> food_regime initial_volume width
#> <fct> <dbl> <dbl>
#> 1 Initial 3.5 0.01
#> 2 Initial 5 0.02
#> 3 Initial 8 0.061
#> 4 Initial 10 0.051
#> 5 Initial 13 0.041
#> 6 Initial 13 0.061
#> 7 Initial 15 0.041
#> 8 Initial 15 0.071
#> 9 Initial 16 0.092
#> 10 Initial 17 0.051
#> # ℹ 62 more rows海胆データはティブル(tibble)形式です。ティブルについて初めて知る方は、『R for Data Science』のティブルに関する章から始めるのが良いでしょう。このデータセットには72個の海胆に関する以下の情報が含まれています:
給餌方法の実験グループ (food_regime):Initial、Low、または High のいずれか
実験開始時のサイズ (initial_volume):ミリリットル単位
実験終了時の縫合幅 (width)
これらの情報を使用して、海胆の成長に対する給餌方法の影響を分析します。
ggplot(urchins,
aes(x = initial_volume,
y = width,
group = food_regime,
col = food_regime)) +
geom_point() +
geom_smooth(method = lm, se = FALSE) +
scale_color_viridis_d(option = "plasma", end = .7)
#> `geom_smooth()` using formula = 'y ~ x'
実験の開始時にボリュームが大きかった海胆は、実験終了時に縫合幅が広い傾向がありますが、傾きが異なるように見えるため、この効果は給餌方法の条件によって異なる可能性があります。
モデルの作成と適合
このデータセットには連続的な予測変数とカテゴリカルな予測変数があるため、標準的な二元分散分析(ANOVA)モデルが適しています。傾きが少なくとも2つの給餌方法で異なるように見えるので、二元交互作用を考慮したモデルを構築します。
width ~ initial_volume * food_regime #これで交互作用項作成初期ボリュームに依存する回帰モデルを作成し、それぞれの給餌方法に対して異なる傾きと切片を持たせます。このようなモデルには、最小二乗法(OLS)が適しています。tidymodels を使用して、まず parsnip パッケージでモデルの機能形式を指定します。数値結果があり、モデルは傾きと切片が線形であるべきなので、モデルタイプは「線形回帰」です。
linear_reg() %>%
set_engine("keras")
#> Linear Regression Model Specification (regression)
#>
#> Computational engine: keraslinear_reg() のドキュメントページには使用可能なすべてのエンジンが記載されています。ここでは、デフォルトエンジンを使用したモデルオブジェクトを lm_mod として保存します。
lm_mod <- linear_reg()ここから、fit() 関数を使用してモデルを推定またはトレーニングすることができます。
lm_fit <-
lm_mod %>%
fit(width ~ initial_volume * food_regime, data = urchins)
lm_fit
#> parsnip model object
#>
#>
#> Call:
#> stats::lm(formula = width ~ initial_volume * food_regime, data = data)
#>
#> Coefficients:
#> (Intercept) initial_volume
#> 0.0331216 0.0015546
#> food_regimeLow food_regimeHigh
#> 0.0197824 0.0214111
#> initial_volume:food_regimeLow initial_volume:food_regimeHigh
#> -0.0012594 0.0005254tidy() 関数は、モデルのパラメータ推定値と統計的特性を整然とした形式で提供します。lm モデルオブジェクトと組み合わせて使用することで、これらの情報を取得できます。以下はその使い方です:
tidy(lm_fit)
#> # A tibble: 6 × 5
#> term estimate std.error statistic p.value
#> <chr> <dbl> <dbl> <dbl> <dbl>
#> 1 (Intercept) 0.0331 0.00962 3.44 0.00100
#> 2 initial_volume 0.00155 0.000398 3.91 0.000222
#> 3 food_regimeLow 0.0198 0.0130 1.52 0.133
#> 4 food_regimeHigh 0.0214 0.0145 1.47 0.145
#> 5 initial_volume:food_regimeLow -0.00126 0.000510 -2.47 0.0162
#> 6 initial_volume:food_regimeHigh 0.000525 0.000702 0.748 0.457この種の出力は、dotwhisker パッケージを使用して回帰結果の点およびウィスカープロットを生成するために使用できます。
tidy(lm_fit) %>%
dwplot(dot_args = list(size = 2, color = "black"),
whisker_args = list(color = "black"),
vline = geom_vline(xintercept = 0, colour = "grey50", linetype = 2))
lm_fitオブジェクトには、lmモデルの出力が組み込まれており、lm_fit$fitでアクセスできます。しかし、予測に関する場合、適合したparsnipモデルオブジェクトを使用することにはいくつかの利点があります。
例えば、出版物において、初期体積が20mlの海胆の平均体サイズをプロットすることが特に興味深い場合を考えてみましょう。このようなグラフを作成するために、新しい例のデータから予測を行います。
new_points <- expand.grid(initial_volume = 20,
food_regime = c("Initial", "Low", "High"))
new_points
#> initial_volume food_regime
#> 1 20 Initial
#> 2 20 Low
#> 3 20 High予測結果を取得するには、predict() 関数を使用して20mlの平均値を見つけます。
変動性を伝えることも重要ですので、予測された信頼区間も見つける必要があります。もし直接lm()を使用してモデルを適合させた場合、predict.lm() のドキュメントページを数分読むだけで、これを行う方法が説明されています。しかし、海胆のサイズを推定するために異なるモデルを使用することを決定した場合(ネタバレ:そうします!)、完全に異なる構文が必要になる可能性があります。
しかし、tidymodelsを使用すると、予測された値のタイプが標準化されているため、これらの値を取得するために同じ構文を使用できます。
まず、平均体幅の値を生成しましょう:
mean_pred <- predict(lm_fit, new_data = new_points)
mean_pred
#> # A tibble: 3 × 1
#> .pred
#> <dbl>
#> 1 0.0642
#> 2 0.0588
#> 3 0.0961予測を行う際、tidymodelsの慣習は常に標準化された列名の結果を含むtibbleを生成することです。これにより、元のデータと予測を使いやすい形式で組み合わせることが容易になります。
conf_int_pred <- predict(lm_fit,
new_data = new_points,
type = "conf_int")
conf_int_pred
#> # A tibble: 3 × 2
#> .pred_lower .pred_upper
#> <dbl> <dbl>
#> 1 0.0555 0.0729
#> 2 0.0499 0.0678
#> 3 0.0870 0.105Now combine:plot_data <-
new_points %>%
bind_cols(mean_pred) %>%
bind_cols(conf_int_pred)and plot:ggplot(plot_data, aes(x = food_regime)) +
geom_point(aes(y = .pred)) +
geom_errorbar(aes(ymin = .pred_lower,
ymax = .pred_upper),
width = .2) +
labs(y = "urchin size")
MODEL WITH A DIFFERENT ENGINE
チームの誰もが満足しているプロットがありますが、ベイズ解析に関する最初の本を読んだ人が1人います。彼らは、モデルをベイズ的なアプローチを使用して推定した場合、結果が異なるかどうかを知りたいと考えています。このような分析では、各モデルパラメータに対して事前分布を宣言する必要があります。事前分布は、パラメータの可能な値(観測データにさらされる前の値)を表します。議論の後、グループは事前分布がベル型であるべきだと合意しましたが、値の範囲がわからないため、保守的なアプローチを取り、事前分布を広くすることにしました。これには、Cauchy分布を使用します(これは自由度が1のt分布と同じです)。
rstanarmパッケージのドキュメントによると、stan_glm()関数を使用してこのモデルを推定することができ、指定する必要がある関数引数はpriorとprior_interceptと呼ばれます。実際には、linear_reg()にstanエンジンがあることがわかりました。これらの事前分布引数は、Stanソフトウェア固有のものであるため、parsnip::set_engine()に引数として渡されます。その後は、同じfit()関数を使用します。
#set the prior distribution
prior_dist <- rstanarm::student_t(df = 1)set.seed(123)
make the parsnip model
bayes_mod <-linear_reg() %>%
set_engine("stan",prior_intercept = prior_dist,prior = prior_dist) #train the model
bayes_fit <-bayes_mod %>%
fit(width ~ initial_volume * food_regime, data = urchins)print(bayes_fit, digits = 5)
#> parsnip model object#>#> stan_glm
#> family: gaussian [identity]
#> formula: width ~ initial_volume * food_regime#> observations: 72
#> predictors: 6#> ------#> Median MAD_SD
#> (Intercept) 0.03277 0.00949
#> initial_volume 0.00156 0.00040
#> food_regimeLow 0.02015 0.01314
#> food_regimeHigh 0.02190 0.01434
#> initial_volume:food_regimeLow -0.00128 0.00052
#> initial_volume:food_regimeHigh 0.00049 0.00071
#>#> Auxiliary parameter(s):
#> Median MAD_SD#> sigma 0.02141 0.00193
#>#> ------
#> * For help interpreting the printed output see ?print.stanreg
#> * For info on the priors used see ?prior_summary.stanregこの種のベイズ解析(多くのモデルと同様)では、適合手続きにランダムに生成された数値が含まれています。set.seed()を使用して、このコードを実行するたびに同じ(擬似)ランダムな数値が生成されるようにします。数字の123は特別なものでもデータに関連しているわけでもありません。これは単にランダムな数値を選択するために使用される「種」です。
パラメータテーブルを更新するには、再度 tidy() メソッドを使用します。
tidy(bayes_fit, conf.int = TRUE)
#> # A tibble: 6 × 5
#> term estimate std.error conf.low conf.high
#> <chr> <dbl> <dbl> <dbl> <dbl>
#> 1 (Intercept) 0.0328 0.00949 0.0160 0.0491
#> 2 initial_volume 0.00156 0.000396 0.000876 0.00226
#> 3 food_regimeLow 0.0201 0.0131 -0.00119 0.0425
#> 4 food_regimeHigh 0.0219 0.0143 -0.00227 0.0457
#> 5 initial_volume:food_regimeLow -0.00128 0.000519 -0.00217 -0.000422
#> 6 initial_volume:food_regimeHigh 0.000491 0.000713 -0.000666 0.00167tidymodelsパッケージの目標の1つは、共通のタスクへのインターフェースを標準化することです(上記のtidy()の結果で見られます)。予測を取得する場合も同様で、基礎となるパッケージが非常に異なる構文を使用していても、同じコードを使用できます。
bayes_plot_data <-
new_points %>%
bind_cols(predict(bayes_fit, new_data = new_points)) %>%
bind_cols(predict(bayes_fit, new_data = new_points, type = "conf_int"))ggplot(bayes_plot_data, aes(x = food_regime)) +
geom_point(aes(y = .pred)) +
geom_errorbar(aes(ymin = .pred_lower, ymax = .pred_upper), width = .2) +
labs(y = "urchin size") +
ggtitle("Bayesian model with t(1) prior distribution")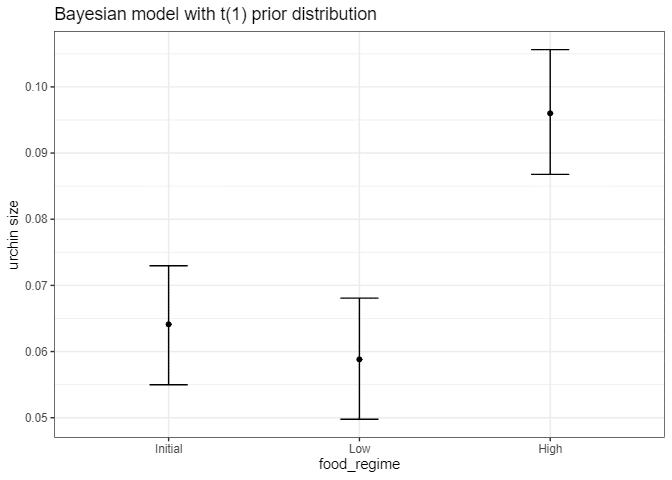
この結果は、非ベイズ結果とあまり変わりません(解釈を除いて)。
注記:parsnipパッケージは多くのモデルタイプ、エンジン、引数と連携できます。使用可能なものを確認するには、tidymodels.org/find/parsnip をご覧ください。
WHY DOES IT WORK THAT WAY?
linear_reg()などの関数を使用してモデルを定義する余分な手順は、lm()を呼び出すよりもはるかに簡潔です。ただし、標準のモデリング関数の問題は、実行から行いたいことを分離していないことです。たとえば、式の実行プロセスは、式が変更されない場合でも、モデルの呼び出しごとに繰り返し実行する必要があります。その計算を再利用することはできません。
また、tidymodelsフレームワークを使用すると、モデルを徐々に作成することでいくつかの興味深いことを行うことができます(単一の関数呼び出しを使用する代わりに)。tidymodelsを使用したモデルのチューニングでは、モデルの部分をチューニングするためにモデルの指定を使用します。これは、linear_reg()がすぐにモデルを適合させた場合に非常に難しいことです。
tidyverseに慣れている場合、モデリングコードがmagrittrパイプ(%>%)を使用していることに気付いたかもしれません。dplyrや他のtidyverseパッケージでは、すべての関数がデータを最初の引数として受け取るため、パイプがうまく機能します。例えば:
urchins %>%
group_by(food_regime) %>%
summarize(med_vol = median(initial_volume))
#> # A tibble: 3 × 2
#> food_regime med_vol
#> <fct> <dbl>
#> 1 Initial 20.5
#> 2 Low 19.2
#> 3 High 15一方、モデリングコードでは、パイプを使用してモデルオブジェクトを渡します。
bayes_mod %>%
fit(width ~ initial_volume * food_regime, data = urchins)これは、dplyrを多く使用してきた場合には少し違和感を覚えるかもしれませんが、ggplot2の動作と非常に似ています。
ggplot(urchins,
aes(initial_volume, width)) + # returns a ggplot object
geom_jitter() + # same
geom_smooth(method = lm, se = FALSE) + # same
labs(x = "Volume", y = "Width") # etc