
Processing でグラフを描く④ 極座標(螺旋と2次曲線)
Processing でグラフを描く 第4回目になります。
いままでは直交座標系を使って、グラフを描いてきました。今回は「極座標」といわれる別の座標系でグラフを描いていきます。我々は「直交座標系」に慣れているので、初めはとっつきにくいかもしれませんが、慣れたら簡単です。座標系は無数にあり、描きたい図形によって便利な座標系を選べばよいのです。
では早速始めましょう。
極座標を描く
BACKGROUND_COLOR = color(0, 44, 77)
colors = [
[255, 255, 255], # white
[255, 127, 0], # orange
[255, 0, 255], # magenta
[127, 127, 255], # lightblue
[255, 255, 0], # yellow
[0, 255, 0], # lime
[255, 127, 127], # pink
[127, 127, 127], # gray
[191, 191, 191], # lightgray
[0, 255, 255], # cyan
[127, 0, 127], # purple
[0, 0, 255], # blue
[127, 0, 0], # brown
[0, 127, 0], # green
[255, 0, 0], # red
[0, 0, 0], # black
]
SIZE = 1000
STEP = 50
RADIUS = 300
points = []
def setup():
global points
size(SIZE, SIZE)
# グラフのデータ
points = []
def draw():
background(BACKGROUND_COLOR)
noFill()
strokeWeight(2)
pushMatrix()
translate(width / 2, height / 2)
stroke(0, 255, 0, 50)
for i in range(0, 360, 15):
line(0, 0, 1000 * cos(radians(i)), 1000 * sin(radians(i)))
for i in range(1, 1000, STEP):
ellipse(0, 0, i * 2, i * 2)
stroke(0, 255, 0)
line(-2000, 0, 2000, 0)
line(0, -2000, 0, 2000)
popMatrix()
極座標を描いてみると、なにか見たことのある図形が現れました。戦争物の映画などに出てくる「レーダー」と同じです。「20時の方向、距離500、敵影発見!」なんてセリフを聞いたことがあると思います。
極座標は自分の位置を基準(原点)として、長さと方角で位置を示します。直感的に位置を捉えられるという特徴があります。戦闘機や艦船の位置表示に使われるのは、そのためです。
直交座標と極座標の相互変換
def draw():
background(BACKGROUND_COLOR)
noFill()
strokeWeight(2)
stroke(0, 255, 0, 50)
for i in range(int(SIZE / STEP)):
line(-2000, i * STEP, 2000, i * STEP)
line(i * STEP, -2000, i * STEP, 2000)
pushMatrix()
translate(width / 2, height / 2)
stroke(0, 255, 0, 50)
for i in range(0, 360, 15):
line(0, 0, 1000 * cos(radians(i)), 1000 * sin(radians(i)))
for i in range(1, 1000, STEP):
ellipse(0, 0, i * 2, i * 2)
stroke(0, 255, 0)
line(-2000, 0, 2000, 0)
line(0, -2000, 0, 2000)
# 直交座標との相互変換
fill(colors[1][0], colors[1][1], colors[1][2])
noStroke()
ellipse(375 * cos(radians(30)), -375 * sin(radians(30)), 10, 10)
stroke(colors[0][0], colors[0][1], colors[0][2])
noFill()
line(0, 0, 375 * cos(radians(30)), -375 * sin(radians(30)))
stroke(colors[0][0], colors[0][1], colors[0][2], 100)
line(375 * cos(radians(30)), 0, 375 * cos(radians(30)), -375 * sin(radians(30)))
line(0, -375 * sin(radians(30)), 375 * cos(radians(30)), -375 * sin(radians(30)))
arc(0, 0, 110 * 2, 110 * 2, radians(330), radians(360))
fill(255)
textSize(40)
text('y', 10, -200)
text('x', 330, -10)
text('r', 150, -100)
text(u'\u03B8', 110, -20)
popMatrix()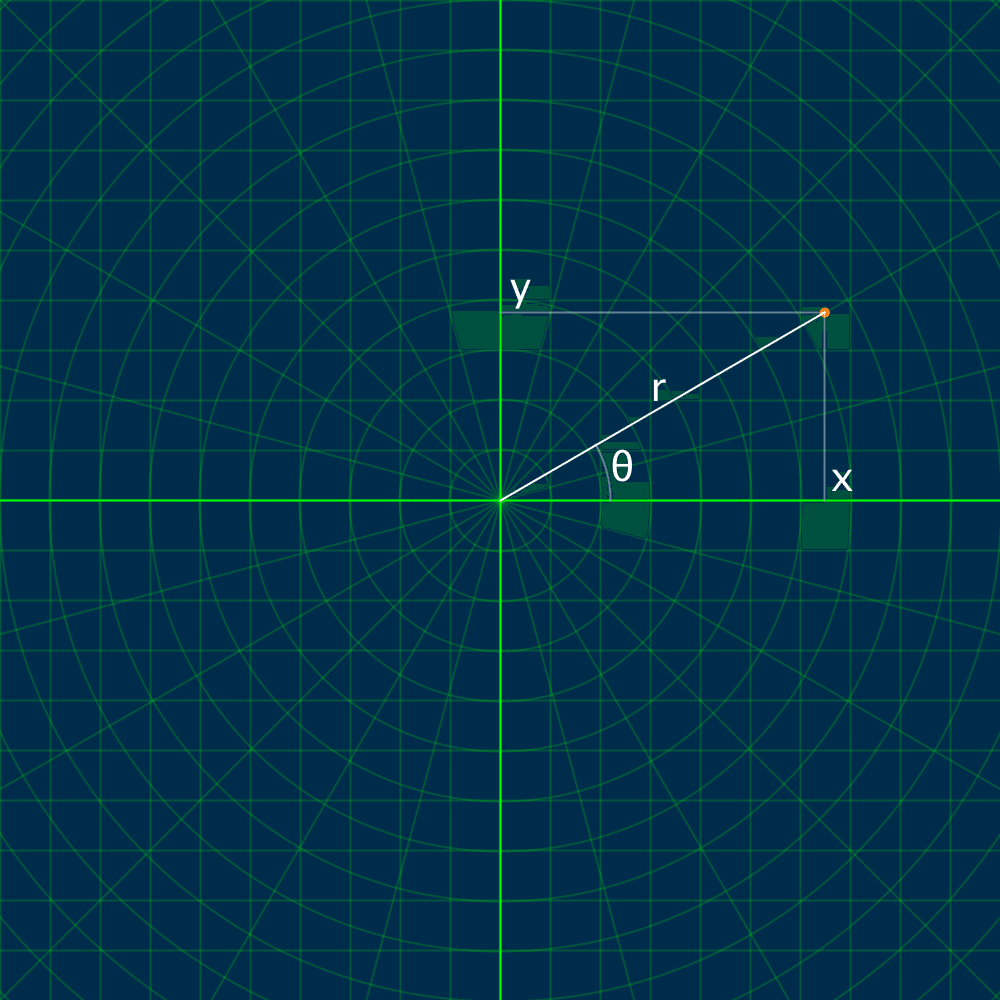
直交座標系と極座標系の相互変換を考えてみます。2次元平面上の位置を表すには2つの値が必要です。直交座標系では「長さ2つ」で、極座標系では「長さと角度」で位置を指定します。
極座標を直交座標に変換
$$
x = r cos(\theta)\\
y = r sin(\theta)
$$
直交座標を極座標に変換
$$
r = \sqrt{x^2 + y^2}\\
tan(\theta) = \frac{y}{x}
$$
アルキメデスの螺旋(らせん)を描く
def setup():
global points
size(SIZE, SIZE)
# グラフのデータ
points = [
[archimedean_spiral(i, 1.0 / 2) for i in range(360 * 4)],
[archimedean_spiral(i, 2.0 / 3) for i in range(360 * 4)],
[archimedean_spiral(i, 1) for i in range(360 * 4)],
[archimedean_spiral(i, 3.0 / 2) for i in range(360 * 4)],
[archimedean_spiral(i, 2) for i in range(360 * 4)],
]
def draw():
background(BACKGROUND_COLOR)
noFill()
strokeWeight(2)
pushMatrix()
translate(width / 2, height / 2)
stroke(0, 255, 0, 50)
for i in range(0, 360, 15):
line(0, 0, 1000 * cos(radians(i)), 1000 * sin(radians(i)))
for i in range(1, 1000, STEP):
ellipse(0, 0, i * 2, i * 2)
stroke(0, 255, 0)
line(-2000, 0, 2000, 0)
line(0, -2000, 0, 2000)
# グラフを描く
count = min(frameCount - 1, 360 * 4 - 1)
for j, p in enumerate(points):
stroke(colors[j][0], colors[j][1], colors[j][2])
for i in range(count):
r1 = p[i]
x1 = r1 * cos(radians(i))
y1 = r1 * sin(radians(i))
r2 = p[i + 1]
x2 = r2 * cos(radians(i + 1))
y2 = r2 * sin(radians(i + 1))
line(x1, -y1, x2, -y2)
else:
stroke(colors[0][0], colors[0][1], colors[0][2], 50)
line(0, 0, 1000 * cos(radians(i)), -1000 * sin(radians(i)))
popMatrix()
def archimedean_spiral(degree_angle, a):
return a * radians(degree_angle) * STEP
アルキメデスの螺旋(渦巻線)は、極座標で描くことができる有名な図形です。$${r = a \theta (a > 0, \theta \geqq 0)}$$ で定義されます。グラフは、a の値を $${\frac{1}{2}, \frac{2}{3}, 1, \frac{3}{2}, 2}$$ に変化させて、5本の線を描きました。
2次曲線を描く
def setup():
global points
size(SIZE, SIZE)
frameRate(5)
# グラフのデータ
for j in range(100):
points.append(
[quadratic_curve(i, RADIUS, j * 0.1) for i in range(360)]
)
def draw():
background(BACKGROUND_COLOR)
noFill()
strokeWeight(2)
pushMatrix()
translate(width / 2, height / 2)
stroke(0, 255, 0, 50)
for i in range(0, 360, 15):
line(0, 0, 1000 * cos(radians(i)), 1000 * sin(radians(i)))
for i in range(1, 1000, STEP):
ellipse(0, 0, i * 2, i * 2)
stroke(0, 255, 0)
line(-2000, 0, 2000, 0)
line(0, -2000, 0, 2000)
# グラフを描く
count1 = min(frameCount - 1, len(points) - 1)
p = points[count1]
stroke(colors[0][0], colors[0][1], colors[0][2])
for i in range(360 - 1):
r1 = p[i]
x1 = r1 * cos(radians(i))
y1 = r1 * sin(radians(i))
r2 = p[i + 1]
x2 = r2 * cos(radians(i + 1))
y2 = r2 * sin(radians(i + 1))
if abs(r1) < height and abs(r2) < height:
line(x1, -y1, x2, -y2)
popMatrix()
def quadratic_curve(i, l, e):
try:
return float(l) / (1 + e * cos(radians(i)))
except ZeroDivisionError:
return 10**10
2次曲線とは「円、楕円、放物線、双曲線」の総称です。極座標を使うと、2次曲線を1つの式で表すことができます。一見バラバラなグラフが一つの式で示せるなんて驚きです。これぞ数学の醍醐味といえるでしょう。
$$
r = \frac{l}{ 1 + e cos{\theta}}\\
e = 0 のとき 円\\
0 < e < 1 のとき 楕円\\
e = 1 のとき 放物線\\
1 < e のとき 双曲線
$$
どうも信用できないので、Processing で検証してみました。その結果のグラフを示します。定義通り、「円、楕円、放物線、双曲線」を描くことができました。(定義の中に cos が含まれているため、横向きに移動します。では sin に変えてみたら?)
グラフだと直感的に定義を捉えることができます。ただし厳密に証明するのは数式の変形が必要になります。たとえば、e = 0 のとき、確かに「円」のように見えますが、本当に「円」であるかはわからないですね。
この記事で数式を変形して、定義が正しいことを示すこともできますが、力尽きてしまいました。数式による証明は読者諸氏にお任せすることにいたしましょう。以上で「極座標」を終わります。
前の記事
Processing でグラフを描く③ 円と楕円
次の記事
Processing でグラフを描く⑤ バラ曲線
その他のタイトルはこちら
