
【二項定理】 〈4〉 等式の証明
今回のシリーズでは、【二項定理】について解説します。
4回目は、等式の証明 のうちで、二項定理を用いるものについて解説しましょう。
〈等式の証明方法〉
中学校のときから、「証明は苦手」「証明が出たらパス!」って人もいたんじゃないかな。
[Method] 証明の代表的手法
① 左辺=……=……=右辺 (左辺を変形していって右辺にする)
② 左辺=……=……=A
右辺=……=……=A (それぞれを変形してい同じ式にする)
③ 左辺ー右辺=……=……=0 (差を考えて0を導く)
④ 左辺/右辺=……=……=1 (割り算を考えて1を導く)
⑤ 自明な等式を変形していく(二項定理、相加相乗平均など)
このMethod の中では、7割くらいが①、1割くらいが②で解決します。
ところが、入試問題では、③~⑤が出題されることも少なくありません。
やっかいですよね。(英語で不規則動詞が出題されるようなものです)
⑤の解法の代表例が、この二項定理です。
例題を見てみましょう。

[Method]
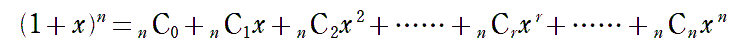
上式は、二項定理に、1とxを代入した式です。
この式を基本として、いくつもの等式が証明できます。
ここから先は
357字
/
9画像
この記事のみ
¥
110
期間限定!Amazon Payで支払うと抽選で
Amazonギフトカード5,000円分が当たる
Amazonギフトカード5,000円分が当たる
この記事が気に入ったらチップで応援してみませんか?
