
【人文情報学散歩(7)】 ネットワーク分析: 「重心性」と「重み」‐ 第2回
1. はじめに

こんにちは、今日は多様な中心性と重みについて、勉強します。その人は組織で重要な人だとしたら、どのような側面で重要な人なのか、それぞれ違うと思いませんか? ネットワーク分析の中心性の概念は、まさにそのような私たちの日常的な考えを具体的な数値に基づいて視覚化するため、非常に有用な分析手法だと思います。
また、彼は彼と関係がある、あるいは友好的である、あるいは非常に友好的である、顔見知りのサイダー程度の様々な関係の強さも言えますよね。 これが重み付けという概念を示しています。このように、中心性と重みは私たちの日常と密接に結びついているため、様々な分析に活用することができます。
2. コード作成
import networkx as nx
import matplotlib.pyplot as plt
import matplotlib.font_manager as fm
# Creating a directed graph
DG = nx.DiGraph()
DG.add_nodes_from([
("Lee", {"age": 30, "gender": "Male", "country": "Korea"}),
("Choi", {"age": 28, "gender": "Female", "country": "Korea"}),
("Jeong", {"age": 35, "gender": "Male", "country": "Korea"}),
("Kito", {"age": 32, "gender": "Female", "country": "Japan"}),
("Kim", {"age": 28, "gender": "Male", "country": "Korea"}),
("Yoon", {"age": 29, "gender": "Male", "country": "Korea"}),
("Ahn", {"age": 27, "gender": "Female", "country": "Korea"}),
("Kang", {"age": 31, "gender": "Male", "country": "Korea"}),
("Hwang", {"age": 30, "gender": "Female", "country": "Korea"}),
("Jung", {"age": 32, "gender": "Male", "country": "Korea"}),
("Nam", {"age": 29, "gender": "Female", "country": "Korea"}),
("Lim", {"age": 28, "gender": "Male", "country": "Korea"}),
("Oh", {"age": 34, "gender": "Female", "country": "Korea"}),
("Seo", {"age": 30, "gender": "Male", "country": "Korea"}),
("Kwon", {"age": 28, "gender": "Female", "country": "Korea"}),
("Kang", {"age": 33, "gender": "Male", "country": "Korea"}),
])
DG.add_edges_from([
("Lee", "Choi", {"relation_type": "Friend", "weight": 1.2}),
("Choi", "Kito", {"relation_type": "Colleague", "weight": 0.4}),
("Jeong", "Kito", {"relation_type": "Friend", "weight": 0.8}),
("Kito", "Lee", {"relation_type": "Friend", "weight": 1.4}),
("Lee", "Kito", {"relation_type": "Friend", "weight": 1.8}),
("Kim", "Kito", {"relation_type": "Family", "weight": 0.8}),
("Kito", "Jeong", {"relation_type": "Colleague", "weight": 0.2}),
("Kito", "Kim", {"relation_type": "Family", "weight": 0.9}),
("Kito", "Yoon", {"relation_type": "Colleague", "weight": 0.3}),
("Yoon", "Kito", {"relation_type": "Colleague", "weight": 0.2}),
("Yoon", "Choi", {"relation_type": "Friend", "weight": 0.3}),
("Ahn", "Choi", {"relation_type": "Friend", "weight": 0.8}),
("Choi", "Hwang", {"relation_type": "Colleague", "weight": 1.6}),
("Hwang", "Jung", {"relation_type": "Friend", "weight": 3.0}),
("Jung", "Nam", {"relation_type": "Family", "weight": 0.9}),
("Nam", "Lim", {"relation_type": "Friend", "weight": 0.1}),
("Lim", "Oh", {"relation_type": "Colleague", "weight": 0.5}),
("Oh", "Seo", {"relation_type": "Colleague", "weight": 0.5}),
("Seo", "Kwon", {"relation_type": "Friend", "weight": 0.8}),
("Kito", "Ahn", {"relation_type": "Friend", "weight": 0.7}),
("Jeong", "Nam", {"relation_type": "Colleague", "weight": 0.6}),
("Nam", "Kang", {"relation_type": "Colleague", "weight": 0.8}),
("Kang", "Kwon", {"relation_type": "Friend", "weight": 0.7}),
("Kwon", "Ahn", {"relation_type": "Friend", "weight": 0.6}),
("Kito", "Kang", {"relation_type": "Friend", "weight": 0.9}),
("Choi", "Hwang", {"relation_type": "Colleague", "weight": 0.6}),
("Jung", "Nam", {"relation_type": "Family", "weight": 0.8}),
("Nam", "Lim", {"relation_type": "Friend", "weight": 0.6}),
("Lim", "Oh", {"relation_type": "Colleague", "weight": 0.7}),
("Oh", "Seo", {"relation_type": "Colleague", "weight": 0.5}),
("Seo", "Kwon", {"relation_type": "Friend", "weight": 0.6}),
])
# Extracting edge weights
edge_weights = nx.get_edge_attributes(DG, 'weight').values()
# Calculating Various node centrality
centrality = nx.degree_centrality(DG)
closeness_centrality = nx.closeness_centrality(DG)
betweenness_centrality = nx.betweenness_centrality(DG)
eigenvector_centrality = nx.eigenvector_centrality(DG)
# Sorting nodes by centrality in descending order
sorted_nodes_centrality = sorted(centrality, key=centrality.get, reverse=True)
sorted_nodes_closeness_centrality = sorted(closeness_centrality , key=closeness_centrality.get, reverse=True)
sorted_nodes_betweenness_centrality = sorted(betweenness_centrality, key=betweenness_centrality.get, reverse=True)
sorted_nodes_eigenvector_centrality = sorted(eigenvector_centrality, key=eigenvector_centrality.get, reverse=True)
# Visualizing the complex social network based on node centrality
plt.figure(figsize=(12, 10))
plt.title("Weighted Bidirectional Network with Node Centrality ",fontsize=16, fontweight='bold')
node_size = [centrality[node] * 6000 for node in DG.nodes]
pos = nx.spring_layout(DG)
edge_labels = {(edge[0], edge[1]): edge[2]["weight"] for edge in DG.edges(data=True)}
nx.draw(
DG, pos, with_labels=True, font_size=12, font_weight='bold', node_color='lightcoral', font_color='black',
node_size=node_size, width=list(edge_weights), edge_color='gray'
)
nx.draw_networkx_edge_labels(DG, pos, edge_labels=edge_labels, font_color='red', font_size=12)
plt.show()
# Interpreting metrics
print("\nMetrics")
print("Number of nodes:", DG.number_of_nodes())
print("Number of edges:", DG.number_of_edges())
print("Degree centrality:", sorted_nodes_centrality)
print("closeness_centrality:", sorted_nodes_closeness_centrality )
print("betweenness_centrality", sorted_nodes_betweenness_centrality )
print("Eigenvector centrality:",sorted_nodes_eigenvector_centrality)
print("Average clustering coefficient:", nx.average_clustering(DG))
このコードは、NetworkXライブラリを使用して、重みのある双方向ネットワークを作成し、可視化する例です。また、ネットワーク内の中心性を計算し、可視化します。
ネットワークの作成
DG = nx.DiGraph(): 有向グラフオブジェクトを作成します。
DG.add_nodes_from(): ノードを追加し、各ノードには年齢、性別、国などの属性情報が含まれています。
DG.add_edges_from(): エッジを追加し、各エッジには関係の種類と重みの情報が含まれています。
重みの取得
nx.get_edge_attributes(): ネットワークからエッジの重み情報を抽出します。
さまざまな中心性の計算
nx.degree_centrality(), nx.closeness_centrality(), nx.betweenness_centrality(), nx.eigenvector_centrality(): ネットワーク内の各ノードの中心性を計算します。
各中心性指標に従って、ノードを中心性が高い順に並べ替えます。
ネットワークの可視化
plt.figure(): 新しい図を作成します。
nx.draw(): ネットワークを可視化します。ノードのサイズは中心性に従い、エッジの太さは重みに従って異なります。
nx.draw_networkx_edge_labels(): エッジ上に重み情報を表示します。
ネットワークのメトリクスの出力
ネットワークの基本的なメトリクスを出力します。ノードの数、エッジの数、中心性指標、平均クラスタリング係数などが出力されます。
3. コードの結果と解釈

Metrics
Number of nodes: 15
Number of edges: 25
Degree centrality: ['Kito', 'Choi', 'Nam', 'Lee', 'Jeong', 'Yoon', 'Ahn', 'Kang', 'Kwon', 'Kim', 'Hwang', 'Jung', 'Lim', 'Oh', 'Seo']
closeness_centrality: ['Ahn', 'Kwon', 'Kang', 'Choi', 'Kito', 'Hwang', 'Nam', 'Jung', 'Lee', 'Jeong', 'Kim', 'Yoon', 'Lim', 'Oh', 'Seo']
betweenness_centrality ['Kito', 'Choi', 'Ahn', 'Kwon', 'Nam', 'Kang', 'Jeong', 'Lim', 'Oh', 'Seo', 'Hwang', 'Jung', 'Lee', 'Yoon', 'Kim']
Eigenvector centrality: ['Kito', 'Choi', 'Ahn', 'Kang', 'Lee', 'Jeong', 'Kim', 'Yoon', 'Hwang', 'Kwon', 'Nam', 'Jung', 'Lim', 'Oh', 'Seo']
Average clustering coefficient: 0.09771241830065361次数重心性(Degree Centrality)
ノードの次数中心性が高い順にソートされています。"Kito"が最も中心的で、"Seo"が最も低い中心性を持っています。次数中心性はノードの直接の隣接数を示し、"Kito"は多くの関係を持っていることがわかります。
近接中心性(Closeness Centrality)
接近中心性が高い順にソートされています。"Ahn"が最も中心的で、"Seo"が最も低い中心性を持っています。接近中心性はノードが他のノードとどれだけ近くにあるかを示し、"Ahn"は比較的他のノードと近くにあることがわかります。
媒介中心軸(Betweenness Centrality)
媒介中心性が高い順にソートされています。"Kito"が最も中心的で、"Seo"が最も低い中心性を持っています。媒介中心性はノードが他のノード間の最短経路上にどれだけ位置しているかを示し、"Kito"は異なるノードの間で情報の流れに重要な役割を果たしている可能性があります。
固有ベクトル中心性(Eigenvector Centrality)
固有ベクトル中心性が高い順にソートされています。"Kito"が最も中心的で、"Seo"が最も低い中心性を持っています。固有ベクトル中心性はノードが他の中心的なノードとどれだけ結びついているかを示し、"Kito"は他の中心的なノードと結びついています。
平均クラスタリング係数
ネットワーク全体の平均クラスタリング係数は0.0977です。これは、ノードがどれだけクラスターを形成しているかを示します。係数が0に近いほど、ネットワークがより分散していることを示します。
重み(Weight)
2つのノード間の関係の強度を表します。基本的なグラフは、エッジ(辺)が接続されたノード間のバイナリ関係のみを表現します。しかし、現実世界の多くのネットワークでは、接続されたノード間の関係が異なる強度を持つことがあります。 たとえば、ソーシャルネットワークでは、2人の人物間の関係が「友達」の場合、この友達関係の強度は異なるかもしれません。一部の友達はより頻繁に連絡を取り合い、高い信頼度を持つかもしれません。このような関係の強度を示すのが重みです。重みがあるネットワークでは、通常、接続されたノード間の関係を表すエッジに重みの値が割り当てられます。重みを考慮すると、ネットワーク分析でより正確な結果を得ることができます。たとえば、中心性の測定では、重みを考慮することで関係が強い場合、そのノードが高い中心性の値を持つようになります。これは関連が強いほど、そのノードが重要であることを示します
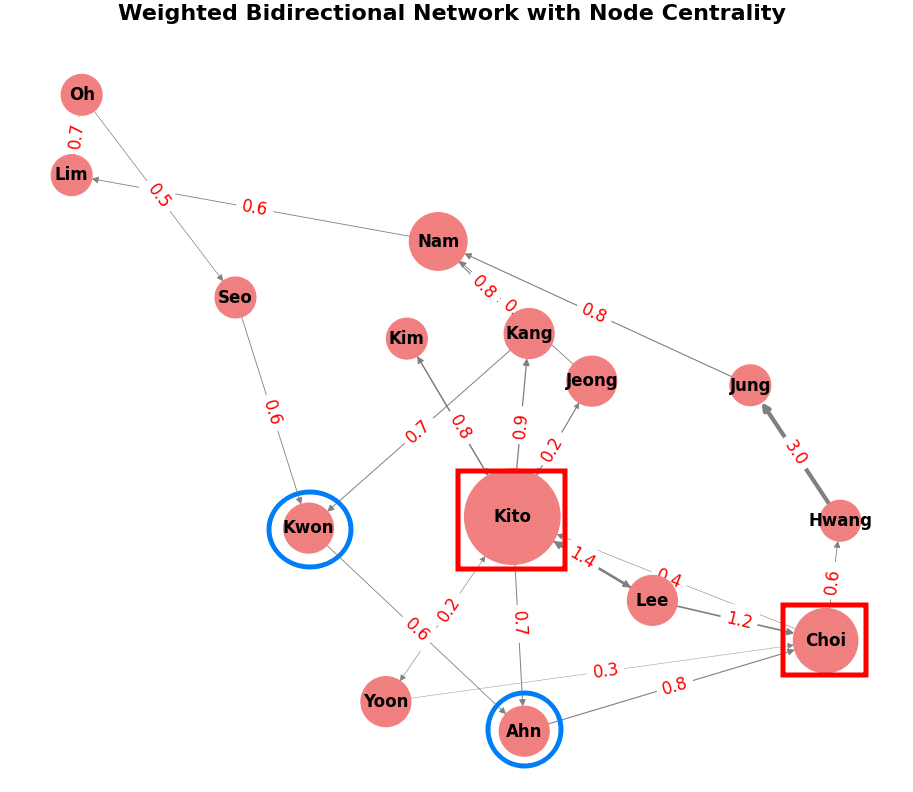
青い丸は2の二位まで表示。
重みが高いと、2つのノード間太くなる。
4. 最後に
今日は中心性の4つの種類と重み付けについて説明しました。 私たちが注目すべき中心性の1つは、いろいろありますが、「意外」の中心性である近接中心性です。先ほど見てきたように、次数中心性ははっきりと目に見えますが、情報伝播において「意外に」重要な役割を果たす人々がネットワーク分析を通じて分かるという点が大きな収穫だと思います!皆さんもそれぞれの日常でネットワーク分析に挑戦して、新しいインサイトを得てください!
デジタル歴史家
ソンさん
