
直動運動する負荷トルクの計算例
ここではモーターの回転による直動系のイナーシャによるモーター負荷トルクついて実際に計算してみます。ワークギヤとモーターギヤのギヤ比が1:1の場合の計算例です。
【直動運動するモーター負荷トルク計算例①】
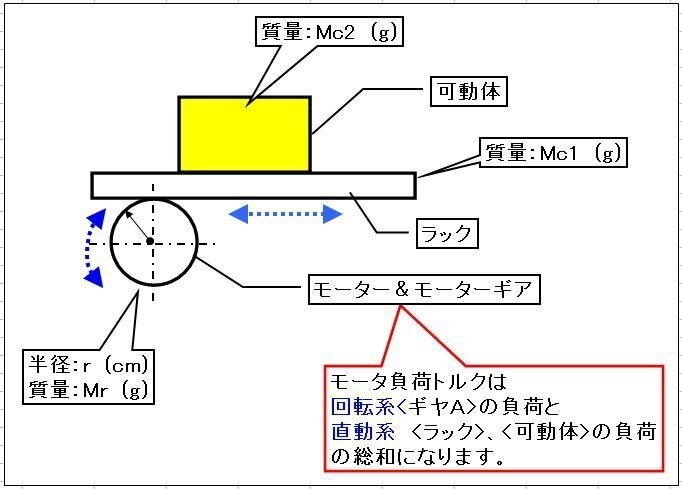
【図-1】ようにラック&ギヤがあり、可動体ワークはラックに固定されています。ギヤはモーターに直結されています。モーターギヤが回転することにより、ラックと可動体ワークが(水平)直動運動します。この時のモーター負荷トルクTを求めましょう。
但し、モーターギヤ半径:r=3(cm)、モーターギヤ質量:Mr=25(g)、ラック質量:Mc1=50(g)、可動体質量:Mc2=200(g)、加速(減速)時間:t1(t3)=0.1(s)、等速時間:t2=0.2(s)、モーター回転角度:θ=450(°)、ラック&可動体移動量:E=4(cm)、モーター1回転当たりの移動量:A=360*4/450=3.2(cm/rev)(A=(360xE/θ)xギヤ比)
モーター負荷トルクTは下記式で求められます。
T=Tr(加速トルク)+Tc(外的負荷トルク)
※外的負荷トルクは主に摩擦トルクのことです。
では、それぞれを求めてみましょう。
※計算例題は全部で4問あります。step毎に複雑化していきますが、この4問を行えば基本はマスターできると思います。
まずは、加速度によって生じる物体のイナーシャによる負荷トルク(Tr)を求めます。この時、回転系の負荷と直動系の負荷に分けて考えます。
回転運動系のイナーシャは、<モーターギヤ>になります。
直動運動系のイナーシャは、<ラックとワーク>になります。
回転運動系イナーシャIr (g・cm・s2)
Ir=(GD2/4)/g=Jr/g
ここで、Jr= Mr x K^2 = Mr x (r^2/2) (g・cm2)
但し、Mr:質量(モーターギヤの質量) (g) r:回転半径(モーターギヤの半径) (cm) g:重力加速度 980 (cm/s2)より、
Ir=25x(3x3/2)/980=0.11 (g・cm・s2) Ir=0.11 (g・cm・s2)
直動運動系イナーシャIc (g・cm・s2)
Ic=(GD2/4)/g=Jc/g
ここで、直動運動する物体のイナーシャ(慣性モーメン)の式
Jc=Mc x (A/2π)^2 (g・cm2)
但し、Mc:質量(ラックとワークの質量) (g) g:重力加速度 980 (cm/s2)
A:単位移動量 (cm/rev) ↑
単位:モーター1回転当たりの移動量(cm)より、
Ic=(50+200)x(3.2/2xπ)x(3.2/2xπ)/980=0.07 (g・cm・s2) Ic=0.07 (g・cm・s2)
よって、加速トルクTrは、
回転系の加速トルク:Tr= Ir xω'=0.11xω'
直動系の加速トルク:Tr= Ic xω'=0.07xω'
但し、Ir :回転運動系 イナーシャ (g・cm・s2) Ic :直動運動系 イナーシャ (g・cm・s2) ω' :モーター 角加速度 (rad/s2)
次にω'を求めます。(最高)角加速度ω' (rad/s2)
基本駆動波形は、【図-2】のような基本台形波です。
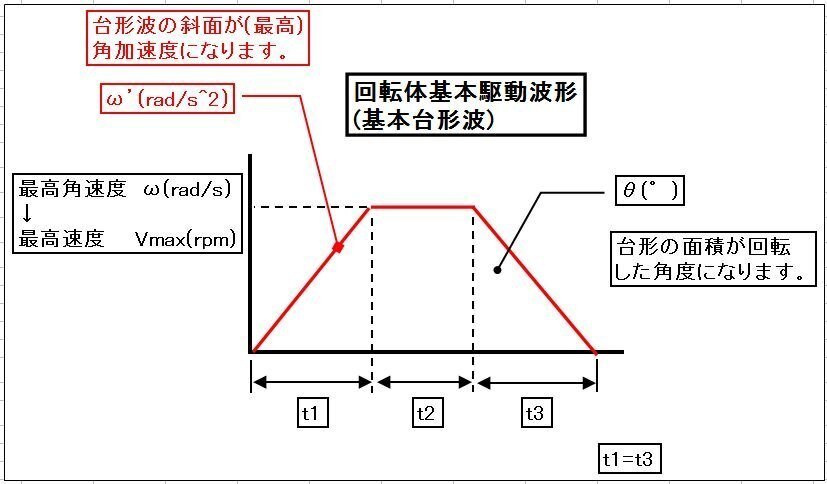
まずは最高角速度ωを求めます。回転角度は台形の面積となるので、 ωx(t1+t2)=θxπ/180 (rad/s)
但し、t1、t2はX軸の時間 (s) θは回転角度 (°)
ω=θxπ/(180x(t1+t2)) (rad/s)より、ω=450xπ/(180x(0.1+0.2))=26.17 (rad/s) ここで、求める最高角加速度ω'は台形波の斜辺となります。
よって、ω'=ω/t1=〔θxπ/180x(t1+t2)〕/t1 (rad/s2)より、ω'=26.17/0.1=261.7 (rad/s2) ω'=261.7 (rad/s2)
よって、
回転系の加速トルク:Tr=Ir xω' =0.11x261.7=28.8 (g・cm)
直動系の加速トルク:Tr=Ic xω' =0.07x261.7=18.3 (g・cm)
次に外的負荷(バネや摩擦など)によって生じる物体の外的負荷トルク(=摩擦トルク)Tcを求めます。
直動運動する外的負荷トルク(摩擦トルク)の式
Tc=F x D/(2 x n x i) (g・cm)
水平の場合:F=Fa+μ x N
Fa:バネ力など、μN:摺動抵抗(Nは垂直抗力)
傾きがある場合:F=Fa+mg x (sinθ +μcosθ)
Fa:バネ力など、mg x sinθ:傾き方向の力、mg x cosθ:垂直方向の力
但し、F:直動運動方向の力 (gf) D:最終(ワーク側)ギヤ直径 (cm) n:効率(0.85~0.95) i:減速比 Fa:外力(バネなど) (gf)
μ:摺動面の摩擦係数(0.05) N:垂直方向荷重(=mg) (gf)
m:ワークとラックの総質量 (g) g:重力加速度 980 (cm/s2)
θ:傾き角度 (°)
【補足】
ラック&ピニオンの場合、中間ギヤを入れてもモータギヤの歯数によって運動が決定する構造です。モータギヤが1歯送るとラックがそのリード分、例えば、3.14mm移動します。中間ギヤはそれを伝達しているだけです。よって、【図-1】のような構造の場合は、減速比はi=1として考えます。中間ギヤは当然回転系のイナーシャに起因しますので、回転系の負荷トルクとして影響しますが、外的負荷トルクには計算上いれなくて良い(実際は摺動抵抗が発生しますが、その分、計算に入れると複雑化してしまうので、ここでは簡易的に省略します)と思います。
但し、実際は中間ギヤが多ければ多い程、伝達力は減少します。一般的にはおもちゃのギヤなどは10~20%down、精密なギヤは、1~2%down程度のdownと言われています。ガタが大きすぎて伝達力が大幅にDOWNする場合は、計算が成立しない場合があります。(理論計算の結果と実際の実験結果で乖離が大きくなってしまうことがよくあります)
では、まずはFを求めます。
F=Fa+μNですが、Faはバネ力などの外力なので今回は作用していないので"0"です。よって、
F=μN=μx mg= 0.05x(50+200)x980=12250x10^-5〔N〕=12.5〔gf〕 F=12.5(gf)
〔単位系比較〕
F=μN=μx mg= 0.05x(0.05+0.2)x9.8=0.1225〔N〕=0.0125〔kgf〕 F=0.0125(kgf)
混乱しやすいので注意が必要です!
上述の式で、摺動抵抗(摩擦力f)がμNとなっています。
摩擦力fは、f=μN=μx mg です。
ここで注意が必要です。fには重力加速度が存在します。単位系が(cm/s2)ですので、単純に(gf)単位とはならないのです。
f=μ x mgの単位系は〔mNまたはN〕
であって、〔gfまたはKgf〕とはならないので注意しましょう。
ちなみに、
●質量の単位が〔kgf〕なら重力加速度gは9.8(m/s2)で、mgは〔N〕
●質量の単位が〔gf〕なら重力加速度gは980(cm/s2)で、mgはx10^-5〔N〕●9.8〔N〕は、1〔kgf〕
以上より、外的(摩擦)負荷トルクが下記のように計算できます。
Tc=F x D/(2 x n x i)
Tc=12.5x (3x2) /(2x0.95x 1) = 39.47 (g・cm) 外的(摩擦)負荷トルク Tc=39.47(g・cm)
ここで考えましょう。直動系の加速トルクと外的(摩擦)負荷トルクについてです。この負荷が【加速時】と【減速時】にモータに負荷をかける方向に働くのか、それともモーターの負荷軽減する方向に働くのか、計算上プラスになるのかマイナスになるか?を考える必要があります。また、【行き】【帰り】についても同様に考える必要があります。
●加速時→【加速トルク】は、モータに負荷をかける方向に働くので、計算上プラスになります。【外的負荷トルク】は、加速しようとしているのにブレーキをかける方向に働きます。つまり、負荷をかける方向に働くため、計算上プラスになります。
●減速時→【減速トルク】も加速トルク同様に、モータに負荷をかける方向に働くので、計算上プラスになります。【外的負荷トルク】は、減速しようとしているものに更にブレーキをかけて助ける方向に働きます。つまり負荷を軽減する方向に働くため、計算上マイナスになります。
●行き、帰り→水平のため、特に考慮しなくても大丈夫ですが、上りや下りのように重力に逆らうような場合は、この部分も考慮する必要があります。
以上より、モーターへの最大負荷は加速時に発生することが分かります。
ここで、上述で計算した結果をまとめます。
回転系の加速トルク Tr=28.8 (g・cm)
直動系の加速トルク Tr=17.3 (g・cm)
外的(摩擦)負荷トルク Tc=39.47(g・cm)
加速時に発生する、モーター最大負荷トルクは、
T= Tr + Tc
Tr:回転&直動系の加速トルク
Tc:外的負荷トルク(=摩擦トルク) より、
T=(28.8+17.3)+39.47=85.57 (g・cm)
モーター最大負荷トルクT=85.57(g・cm)
【補足①】
モーターを選定をする際は、これに安全率を考慮して選定しましょう。一般的には、安全率2倍(S=2)で考えます。上記の計算例の場合、モータを選定する際は、最大加速時に発生する(最高速度到達付近=最高速度pps時)T=85.57x2=171.14(g・cm)を目安に(最大速度時に171.14(g・cm)程度のトルクを持つ)モータを選定するのが良いでしょう。
【補足②】
モーター選定の際は、モーターの許容イナーシャと負荷イナーシの関係を考慮(ステッピングモーターならばイナーシャ比10倍以下)する必要があります。
【直動運動するモーター負荷トルク計算例②】
ここではモーターの回転による直動系のイナーシャによるモーター負荷トルクついて実際に計算してみます。ワークギヤとモーターギヤのギヤ比が異なるの場合の計算例です。
【モーター負荷トルク計算】
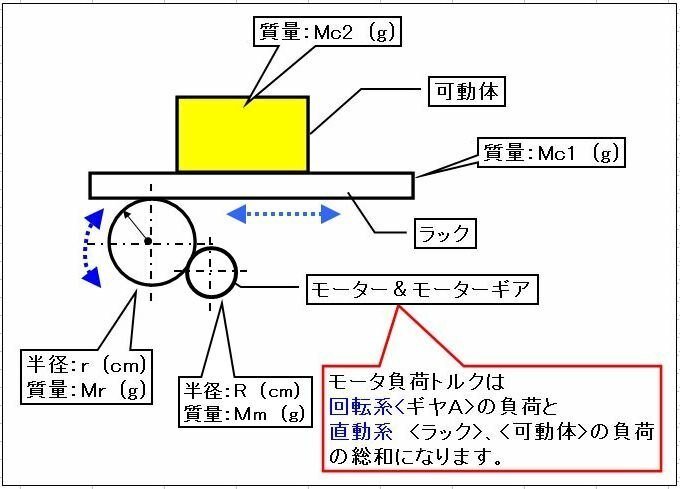
【図-3】ようにラック&ギヤがあり、可動体ワークはラックに固定されています。ギヤはモーターに直結されています。モーターギヤが回転することにより、ラックと可動体ワークが(水平)直動運動します。モーター負荷トルクTを求めましょう。
但し、モーター従動ギヤ半径:r=3(cm)、モーター従動ギヤ質量:Mr=25(g)モーターギヤ半径:R=1.5(cm)、モーターギヤ質量:Mm=12.5(g)、ラック質量:Mc1=50(g)、可動体質量:Mc2=200(g)、加速(減速)時間:t1(t3)=0.1(s)、等速時間:t2=0.2(s)、モーター回転角度:θ=450(°)、ラック&可動体移動量:E=4(cm)、モーター1回転当たりの移動量:A=360x4/450=3.2(cm/rev)(A=(360xE/θ)xギヤ比)
モーター負荷トルクTは下記式で求められます。
T=Tr(加速トルク)+Tc(外的負荷トルク)
※外的負荷トルクは主に摩擦トルクのことです。
それぞれを求めてみましょう。
まずは、加速度によって生じる物体のイナーシャによる
負荷トルク(Tr)を求めます。
この時、回転系の負荷と直動系の負荷に分けて考えます。
回転運動系のイナーシャは、<モーターギヤ>になります。
直動運動系のイナーシャは、<ラックとワーク>になります。
回転運動系イナーシャIr (g・cm・s2)
Ir=(GD^2/4)/g=Jr/g
ここで、Jr= Mr x K^2 = Mr x (r^2/2) (g・cm2)
但し、Mr:質量(モーターギヤの質量) (g) r:回転半径(モーターギヤの半径) (cm)
g:重力加速度 980 (cm/s2) より、
Ir(従動ギヤ)=25x(3x3/2)/980=0.11 (g・cm・s2)
Ir(従動ギヤ)=0.11 (g・cm・s2)
Ir(モーターギヤ)=12.5x(1.5x1.5/2)/980=0.11 (g・cm・s2) Ir(モーターギヤ)=0.01 (g・cm・s2)
直動運動系イナーシャIc (g・cm・s2)
Ic=(GD2/4)/g=Jc/g
ここで、直動運動する物体のイナーシャ(慣性モーメン)の式
Jc=Mc x (A/2π)^2 (g・cm2)
但し、Mc:質量(ラックとワークの質量) (g) g:重力加速度 980 (cm/s2) A:単位移動量 (cm/rev)⇒単位:モーター1回転当たりの移動量(cm)
より、
Ic=(50+200)x(3.2/2xπ)x(3.2/2xπ)/980=0.07 (g・cm・s2) Ic=0.07 (g・cm・s2)
よって、加速トルクTrは、
回転系(従動ギヤ)の加速トルク:
Tr= Ir x(モータギヤ/ワークギヤ)^2 x ω'=0.11 x (1.5/3)x(1.5/3) x ω'
【補足】
従動ギヤが対象で、モーターギヤは直結してるので、ギヤ比は1になります。回転系(モーターギヤ)の加速トルク: Tr= Ir x ω'=0.01 x ω'
直動系の加速トルク: Tr= Ic xω'=0.07 x ω'
但し、Ir:回転運動系 イナーシャ (g・cm・s2) Ic:直動運動系 イナーシャ (g・cm・s2) ω' :モーター 角加速度 (rad/s2)
モーター側とワーク側のギヤ比が異なる場合、(ワーク側の)負荷イナーシャはギヤ比の2乗に比例します。リンクレバーなどを用いて、ワークの移動量を変える場合も同様で、例えばリンク比を1:3にして、ワークの移動量を3倍にした場合、ワークのイナーシャは3の2乗=9倍になります。
直動系のイナーシャの式は、Jc=Mc x (A/2π)^2 (g・cm2)です。
Aは、モーター1回転当たりの移動量なので、2乗に比例していることが、分かります。つまり、回転系でも直動系でも、ギヤやリンクなどを用いて移動量(運動量)を変化させると、イナーシャは、その(変化量)の2乗に比例します。モーター側とワーク側のギヤ比が異なる場合、(モーター軸換算される)負荷トルクの基本式は下記になります。
【回転系負荷トルク】
T= 〔Ir x (モータギヤ/ワークギヤ)^2〕 x ω'
ここで、ワークイナーシャを(ギヤ比に応じて)モーター軸換算して計算してます。
【直動系負荷トルク】
T= Ic x ω'
但し、Ic=Jc/gで、Jc=Mc x (A/2π)^2 です。
ここで、ワークイナーシャを(レバー比に応じて)モーター軸換算して計算してます。 このように、ギヤ比を変えることで、ワークイナーシャを大幅に軽減できます。モーターの許容イナーシャをワークイナーシャが超えないようにするには、有効な手段の1つと言えます。モーターの許容イナーシャとワークイナーシャの関係については、下記を参照して下さい。
ω'を求めます。
(最高)角加速度ω' (rad/s2)
基本駆動波形は、【図-4】のような基本台形波です。
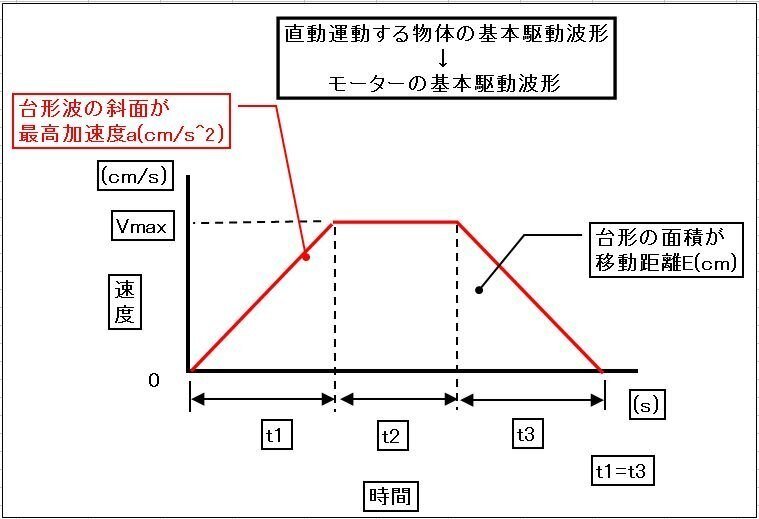
まずは最高角速度ωを求めます。
回転角度は台形の面積となるので、 ωx(t1+t2)=θxπ/180 (rad/s)
但し、t1、t2はX軸の時間 (s) θは回転角度 (°)
ω=θxπ/(180x(t1+t2)) (rad/s) より、
ω=450xπ/(180x(0.1+0.2))=26.17 (rad/s)
ここで、求める最高角加速度ω'は台形波の斜辺となります。
ω'=ω/t1=〔θxπ/180x(t1+t2)〕/t1 (rad/s2)より、
ω'=26.17/0.1=261.7 (rad/s2)
ω'=261.7 (rad/s2)
回転系(従動ギヤ)の加速トルク:
Tr=Ir x(モータギヤ/ワークギヤ)^2 x ω' =(0.11) x (1.5/3)x(1.5/3) x 261.7 =7.20 (g・cm)
回転系(モーターギヤ)の加速トルク:
Tr=Ir x(モータギヤ/ワークギヤ)^2 x ω' =0.01 x 261.7 =2.62 (g・cm)
よって、
回転系の加速トルク:Tr =7.20+2.62=9.82 (g・cm)
直動系の加速トルク:Tr=Ic xω' =0.07x261.7=18.32 (g・cm)
となります。
次に外的負荷(バネや摩擦など)によって生じる物体の外的負荷トルク(=摩擦トルク)Tcを求めます。
直動運動する外的負荷トルク(摩擦トルク)の式
Tc=F x D/(2 x n x i) (g・cm)
水平の場合:F=Fa+μ x N
Fa:バネ力など、μ x N:摺動抵抗(Nは垂直抗力)
傾きがある場合:F=Fa + mg x (sinθ + μcosθ)
Fa:バネ力など、mg x sinθ 傾き方向の力、mg x cosθ 垂直方向の力
但し、F:直動運動方向の力 (gf) D:最終(ワーク側)ギヤ直径 (cm) n:効率(0.85~0.95) i:減速比 Fa:外力(バネなど) (gf) μ:摺動面の摩擦係数(0.05) N:垂直方向荷重(=mg) (gf) m:ワークとラックの総質量 (g) g:重力加速度 980 (cm/s2) θ:傾き角度 (°)
では、まずはFを求めます。F=Fa+μNですが、Faはバネ力などの外力なので今回は作用していないので"0"です。
よって、
F=μN=μx mg= 0.05x(50+200)x980=12250x10-5〔N〕=12.5〔gf〕 F=12.5(gf)
〔単位系比較〕
F=μN=μx mg= 0.05x(0.05+0.2)x9.8=0.1225〔N〕=0.0125〔kgf〕 F=0.0125(kgf)
混乱しやすいので注意が必要です!上述の式で、摺動抵抗(摩擦力f)がμNとなっています。摩擦力fは、f=μN=μx mg です。ここで注意が必要です。fには重力加速度が存在します。単位系が(cm/s2)ですので、単純にgfとはならないのです。f=μ x mgの単位系は〔mNまたはN〕であって、〔gfまたはKgf〕とはならないので注意しましょう。ちなみに、
●質量の単位が〔kgf〕なら重力加速度gは9.8(m/s2)で、mgは〔N〕
●質量の単位が〔gf〕なら重力加速度gは980(cm/s2)で、mgは x10^-5〔N〕●9.8〔N〕は、1〔kgf〕
以上で、外的(摩擦)負荷トルクが下記のように計算できます。
Tc=F x D/(2 x n x i)
ここで、減速比iを考えます。モーターギヤが1回転すると、従動ギヤは1/2回転します。上図のようなラック&ピニオンの構造なので、ラックは従動ギヤから伝達されるため、減速比 i=モータギヤ/従動ギヤ になります。
Tc=12.5x (3x2) /(2x0.95x 1.5/3) = 75/0.95 =78.95 (g・cm) 外的負荷トルク Tc=78.95 (g・cm)
ここで考えましょう。直動系の加速トルクと外的(摩擦)負荷トルクについてです。この負荷が【加速時】と【減速時】にモータに負荷をかける方向に働くのか、それともモーターの負荷軽減する方向に働くのか、計算上プラスになるのかマイナスになるか?を考える必要があります。また、【行き】【帰り】についても同様に考える必要があります。
●加速時→【加速トルク】は、モータに負荷をかける方向に働くので、計算上プラスになります。【外的負荷トルク】は、加速しようとしているのにブレーキをかける方向に働きます。つまり、負荷をかける方向に働くため、計算上プラスになります。
●減速時→【減速トルク】も加速トルク同様に、モータに負荷をかける方向に働くので、計算上プラスになります。【外的負荷トルク】は、減速しようとしているものに更にブレーキをかけて助ける方向に働きます。つまり負荷を軽減する方向に働くため、計算上マイナスになります。
●行き、帰り→水平のため、特に考慮しなくても大丈夫ですが、上りや下りのように重力に逆らうような場合は、この部分も考慮する必要があります。以上より、モーターへの最大負荷は加速時に発生することが分かります。
ここで、上述で計算した結果をまとめます。
回転系の加速トルク Tr=9.82 (g・cm)
直動系の加速トルク Tr=18.32 (g・cm)
外的(摩擦)負荷トルク Tc=78.95(g・cm)
加速時に発生する、モーター最大負荷トルクは、
T= Tr + Tc
Tr:回転&直動系の加速トルク Tc:外的負荷トルク(=摩擦トルク)より、
T=(9.82+18.32)+78.95=107.09 (g・cm)
モーター最大負荷トルクT=107.09(g・cm)
【補足①】
モーターを選定をする際は、これに安全率を考慮して選定しましょう。一般的には、安全率2倍(S=2)で考えます。上記の計算例の場合、モータを選定する際は、最大加速時に発生する(最高速度到達付近=最高速度pps時)T=107.09x2=214.18(g・cm)を目安に(最大速度時に214.18(g・cm)程度のトルクを持つ)モータを選定するのが良いでしょう。
【補足②】
モーター選定の際は、モーターの許容イナーシャと負荷イナーシの関係を考慮(ステッピングモーターならばイナーシャ比10倍以下)する必要があります。
【直動運動するモーター負荷トルク計算例③】
ここでは直動系イナーシャのモーター負荷計算における傾きがある運動で、ワークギヤとモーターギヤのギヤ比が異なる場合の計算例を紹介します。
【モーター負荷トルク計算】
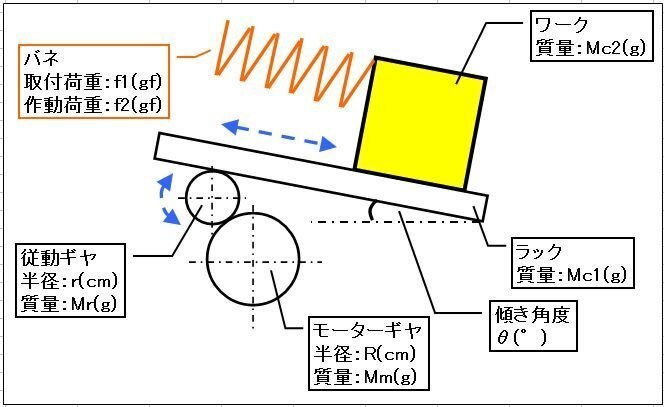
【図-5】ようにラック&ギヤがあり、可動体ワークはラックに固定されています。ギヤはモーターに直結されています。モーターギヤが回転することにより、ラックと可動体ワークが(傾きθ°を保ちながら)直動運動します。モーター負荷トルクTを求めましょう。但し、モーター従動ギヤ半径:r=2(cm)、モーター従動ギヤ質量:Mr=25(g)、モーターギヤ半径:R=4(cm)、モーターギヤ質量:Mm=50(g)、ラック質量:Mc1=50(g)、可動体質量:Mc2=200(g)、加速(減速)時間:t1(t3)=0.1(s)、等速時間:t2=0.2(s)、モーター回転角度:θ=450(°)、ラック&可動体移動量:E=4(cm)、モーター1回転当たりの移動量:A=(360x4/450)x(4/2)=6.4(cm/rev)、バネ力取付時荷重:f1=250(gf) 下り最下点位置でのバネ力、バネ力作動時荷重:f2=350(gf) 上り最上点位置でのバネ力( バネは圧縮コイルバネ(押しバネ)想定)、傾き角度:θ=30(°)
モーター負荷トルクTは下記式で求められます。
T=Tr(加速トルク)+Tc(外的負荷トルク)
※外的負荷トルクは主に摩擦トルクのことです。
T= 〔Ir x (モータギヤ/ワークギヤ)^2〕 x ω'
T= Ic x ω'
Jc=Mc x (A/2π)^2
それぞれを求めてみましょう。まずは、加速度によって生じる物体のイナーシャによる負荷トルク(Tr)を求めます。この時、回転系の負荷と直動系の負荷に分けて考えます。回転運動系のイナーシャは、<モーターギヤ>になります。直動運動系のイナーシャは、<ラックとワーク>になります。
回転運動系イナーシャIr (g・cm・s2)
Ir=(GD^2/4)/g=Jr/g
ここで、Jr= Mr x K^2 = Mr x (r^2/2) (g・cm2)
但し、Mr:質量(モーターギヤの質量) (g) r:回転半径(モーターギヤの半径) (cm)
g:重力加速度 980 (cm/s2) より、
Ir(従動ギヤ)=25x(2x2/2)/980=0.05 (g・cm・s2)
Ir(従動ギヤ)=0.05 (g・cm・s2)
Ir(モーターギヤ)=50x(4x4/2)/980=0.41 (g・cm・s2)
Ir(モーターギヤ)=0.41 (g・cm・s2)
直動運動系イナーシャIc (g・cm・s2)
Ic=(GD2/4)/g=Jc/g
ここで、直動運動する物体のイナーシャ(慣性モーメン)の式
Jc=Mc x (A/2π)^2 (g・cm2)
但し、Mc:質量(ラックとワークの質量) (g) g:重力加速度 980 (cm/s2)
A:単位移動量 (cm/rev)⇒単位:モーター1回転当たりの移動量(cm)より、
Ic=(50+200)x(6.4/2xπ)x(6.4/2xπ)/980=0.26 (g・cm・s2) Ic=0.26 (g・cm・s2)
よって、加速トルクTrは、回転系(従動ギヤ)の加速トルク:
Tr= Ir x(モータギヤ/ワークギヤ)^2 x ω'=0.05 x (4/2)x(4/2) x ω'
【補足】
従動ギヤが対象で、モーターギヤは直結してるので、ギヤ比は1です。
回転系(モーターギヤ)の加速トルク: Tr= Ir x ω'=0.41 x ω'
直動系の加速トルク: Tr= Ic xω'=0.26xω'
但し、Ir :回転運動系 イナーシャ (g・cm・s2) Ic :直動運動系 イナーシャ (g・cm・s2) ω' :モーター 角加速度 (rad/s2)
ω'を求めます。
(最高)角加速度ω' (rad/s2)
基本駆動波形は、【図-7】のような基本台形波です。

まずは最高角速度ωを求めます。回転角度は台形の面積となるので、
ω x (t1+t2) =θ x π/180 (rad/s)
但し、t1、t2はX軸の時間 (s) θは回転角度 (°)
ω=θxπ/(180x(t1+t2)) (rad/s)より、ω=450xπ/(180x(0.1+0.2))=26.17 (rad/s) ここで、求める最高角加速度ω'は台形波の斜辺となります。
ω'=ω/t1=〔θxπ/180x(t1+t2)〕/t1 (rad/s2)より、
ω'=26.17/0.1=261.7 (rad/s2)
ω'=261.7 (rad/s2)
よって、回転系の加速トルク(従動ギヤ):
Tr=Ir x(モータギヤ/ワークギヤ)^2 x ω' =(0.05) x (4/2) x (4/2) x 261.7 =52.34 (g・cm)
回転系の加速トルク(モーターギヤ):
Tr=Ir x ω' =0.41 x 261.7 =107.30 (g・cm)
直動系の加速トルク:Tr=Ic xω' =0.26x261.7=68.04 (g・cm)
次に外的負荷(バネや摩擦など)によって生じる物体の外的負荷トルク(=摩擦トルク)Tcを求めます。直動運動する外的負荷トルク(摩擦トルク)の式
Tc=F x D/(2 x n x i)(g・cm)
水平の場合:F=Fa + μ x N
傾きがある場合:F=Fa + mg x (sinθ + μcosθ)
但し、F:直動運動方向の力 (gf) D:最終(ワーク側)ギヤ直径 (cm) n:効率(0.85~0.95) i:減速比 Fa:外力(バネなど) (gf) μ:摺動面の摩擦係数(0.05) N:垂直方向荷重(=mg) (gf) m:ワークとラックの総質量 (g) g:重力加速度 980 (cm/s2) θ:傾き角度 (°)
では、まずはFを求めます。
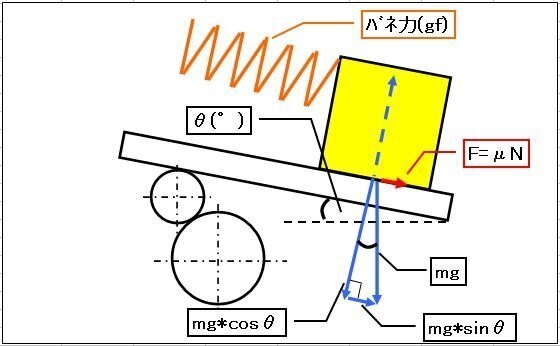
F=Fa+μN より、傾きがあるので、右図からも分かるように、
F= Fa + mg x (sinθ+μcosθ) です。ここで、〔上り〕と〔下り〕でFは異なることに注意します。
●〔上り〕では傾き方向の力mg*sinθは"+"になります。(トルクを助けない方向<モーターに負荷をかける方向>)
●〔下り〕では傾き方向の力mg*sinθは"-"になります。(トルクを助ける方向<モーターに負荷をかけない方向>)
よって、〔上り〕と〔下り〕に分けてそれぞれのFを求めます。
混乱しやすいので注意が必要です!下述の式で、バネ力Faの単位は〔gf〕です。一方、摺動抵抗(摩擦力)mg*(sinθ+μcosθ)の単位は〔N〕です。摺動抵抗(摩擦力)には重力加速度が存在します。単位系が(cm/s2)ですので、単純にgfとはならないのです。f=μ x mgの単位系は〔mNまたはN〕であって、〔gfまたはKgf〕とはならないので注意しましょう。
ちなみに、
●質量の単位が〔kgf〕なら重力加速度gは9.8(m/s2)で、mgは〔N〕
●質量の単位が〔gf〕なら重力加速度gは980(cm/s2)で、mgは x10-5〔N〕●9.8〔N〕は、1〔kgf〕
以下、*はx(掛ける)の意です。
F=Fa+mg*(sinθ+μcosθ)
【上り時のFとTc】
F(上り)=f1〔gf〕 + mg*(sinθ+μcosθ) 〔g・cm/s2〕=350〔gf〕 + (50+200)*980*(sin30+0.05*cos30) 〔g・cm/s2〕=350〔gf〕 + 250*980*(0.5+0.05*0.87) 〔g・cm/s2〕=350〔gf〕 + 133157.5*10-5 〔N〕=350〔gf〕 + 135.875 〔gf〕=485.88 〔gf 〕
〔単位系比較〕
F(上り)=f1〔kgf〕 + mg*(sinθ+μcosθ) 〔Kg・m/s2〕=0.35〔kgf〕+ 0.25*9.8*(0.5+0.05*0.87) 〔Kg・m/s2〕=0.35〔kgf〕+ 1.331575〔N〕=0.35〔kgf〕+ 0.135875〔kgf〕=0.485875〔kgf〕
Tc=〔485.9* (2*2)/(2* 0.95* 4/2) =511.47 (g・cm)
よって、Tc<上り>=511.47 (g・cm)
F=Fa+mg*(sinθ+μcosθ)
【下り時のFとTc】
F(下り)=f2〔gf〕 + mg*(-sinθ+μcosθ) 〔g・cm/s2〕=250〔gf〕 + (50+200)*980*(-sin30+0.05*cos30) 〔g・cm/s2〕=250〔gf〕 + 250*980*(-0.5+0.05*0.87) 〔g・cm/s2〕=250〔gf〕 + (-111842.5*10-5 ) 〔N〕=250〔gf〕 + (-114.125) 〔gf〕=135.875 〔gf〕
〔単位系比較〕
F(下り)=f2〔kgf〕 + mg*(-sinθ+μcosθ) 〔Kg・m/s2〕=0.25〔kgf〕+ 0.25*9.8*(-0.5+0.05*0.87) 〔Kg・m/s2〕=0.25〔kgf〕+ (-1.118425)〔N〕=0.25〔kgf〕+ (-0.114125)〔kgf〕=0.135875〔kgf〕
Tc=〔135.9* (2*2)/(2* 0.95* 4/2 )143.05 (g・cm)
よって、Tc<下り>=143.05 (g・cm)
ここで考えましょう!
直動系の加速トルクと外的(摩擦)負荷トルクについてです。この負荷が【加速時】と【減速時】にモータを助ける方向に働くのか、それとも悪い方向に働くのか、計算上プラスになるのかマイナスになるか?を考える必要があります。また、【上り】【下り】についても同様に考える必要があります。
●上りの加速時
加速トルクはモータに負荷を与える方向に働くので、負荷を増やす方向、つまり計算上プラスになります。バネ力や物体が重力方向に戻ろうとする力(仮に摩擦力と表記します)による外的負荷トルクは、加速しようとしているのにブレーキをかける方向に働きます。つまり、負荷を増やす方向に働くため、計算上プラスになります。加速:プラス(増)、バネ力:プラス(増)、摩擦力:プラス(増)
●上りの減速時
減速トルクも加速トルク同様に、モータに負荷を与える方向に働くので負荷を増やす方向、つまり計算上プラスになります。バネ力や物体が重力方向に戻ろうとする力(仮に摩擦力と表記します)による外的負荷トルクは、減速しようとしているものに更にブレーキをかけて助ける方向に働きます。つまり、負荷を軽減する方向に働くため、計算上マイナスになります。減速:プラス(増)、バネ力:マイナス(減)、摩擦力:マイナス(減)
●下りの加速時
加速トルクはモータに負荷を与える方向に働くので、負荷を増やす方向、つまり計算上プラスになります。バネ力による外的負荷トルクは、加速しようとしているのに更に押す方向に助けるように働きます。つまり、負荷を軽減する方向に働くため、計算上、マイナスになります。物体が重力方向に戻ろうとする力(仮に摩擦力と表記します)による外的負荷トルクは、加速しようとしているのに更に、ブレーキをかけて負荷を増やす方向に働きます。つまり、負荷を増やす方向に働くため、計算上、プラスになります。加速:プラス(増)、バネ:マイナス(減)、摩擦力:プラス(増)
●下りの減速時
減速トルクも加速トルク同様に、モータに負荷を与える方向に働くので負荷を増やす方向、つまり計算上プラスになります。バネ力による外的負荷トルクは、減速しようとしているものに対して更に押す方向に働きます。つまり、負荷を増す方向に働くため、計算上プラスになります。物体が重力方向に戻ろうとする力(仮に摩擦力と表記します)による外的負荷トルクは、減速しようとしているのに更に、ブレーキをかけて助ける方向に働きます。つまり、負荷を助ける方向に働くため、計算上、マイナスになります。減速:プラス(増)、バネ:プラス(増)、摩擦力:マイナス(減)
以上のことより、最大負荷は"上り"の"加速時"に発生 することが分かりました。
【補足】
ただし、厳密には上りの加速時の領域では、バネはまだ縮みだしている最中であり、バネの最大荷重領域には達していないことが推察できます。より精度の高い計算が必要な場合は、加速・減速領域におけるバネのその時点での荷重にてそれぞれ計算を行う必要があり、その比較を行う必要があります。今回は擬似的な最大負荷トルクと言う点で且つ計算を複雑化させずに分りやすくする、と言う意味で"上りの加速時"が負荷が高く、その時のバネ力が最大値に近い、と言う想定で計算します。
ここで、上述で計算した結果をまとめます。
回転系の加速トルク Tr=159.64 (g・cm)
直動系の加速トルク Tr=68.04 (g・cm)
外的(摩擦)負荷トルク(上り) Tc=511.47(g・cm)
外的(摩擦)負荷トルク(下り) Tc=143.05(g・cm)
”上り”の加速時に発生する、モーター最大負荷トルクは、
T= Tr + Tc
Tr:回転&直動系の加速トルク
Tc:外的負荷トルク(=摩擦トルク)より、
T=(159.64+68.04)+511.47=739.15 (g・cm)
モーター最大負荷トルクT=739.15(g・cm)
【補足】
バネ力の妥当性確認が可能です。外的(摩擦)負荷トルク、とりわけこの場合はバネ力(上り511.47g・cm 下り143.05g・cm)と加速(減速)トルク(159.64+68.04=227.68g・cm)を比較した場合、外的負荷トルクが加速トルクを上回る場合、バネなどでそのワークをきちんと押さえつけている(拘束)機構と言えます。加速におけるワークのジャンピングを嫌う機構の場合には、バネを強くして外的負荷トルクを加速トルクより大きくしておくことが大切です。また、バネの力がその機構に対して妥当かどうかの判定も今回のような計算で妥当性の確認が出来ます。計算することは非常に便利で且つ重要だと言えます。今回の計算事例では、上り時を見た時、外的(摩擦)負荷トルク(511.47g・cm)>加速トルク227.68(g・cm)より、バネによってワークを完全に拘束している、と言うことがわかります。下り時を見た時、外的(摩擦)負荷トルク(143.05g・cm)<加速トルク227.68(g・cm) ですが、バネの力の向きが下り時の向きと同じ方向のため、一般的には、特に問題ないと言えると思います。
【直動運動するモーター負荷トルク計算例④】
ここでは直動系イナーシャのモーター負荷計算におけるワーク運動が垂直運動の場合の計算例を紹介します。
【モーター負荷トルク計算】
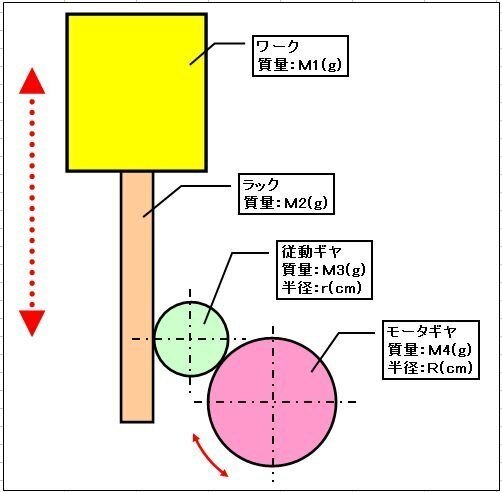
【図-8】ようにラック&ギヤがあり、可動体ワークはラックに固定されています。モーターギヤが回転することにより、ラックと可動体ワークが垂直上下運動します。モーター負荷トルクTを求めましょう。
但し、モーター従動ギヤ半径:r=3(cm)、モーター従動ギヤ質量:M3=30(g)モーター直結ギヤ半径:R=5(cm)、モーター直結ギヤ質量:M4=50(g)、ラック質量:M2=40(g)、可動体質量:M1=600(g)、加速(減速)時間:t1(t3)=0.2(s)、等速時間:t2=0.4(s)、モーター回転角度:θ=720(°)、ラック&可動体移動量:E=10(cm)、モーター1回転当たりの移動量:A=(360x10/720)x(5/3)=8.3(cm)(A=(360xE/θ)xギヤ比)
モーター負荷トルクTは下記式で求められます。
T=Tr(加速トルク)+Tc(外的負荷トルク)
※外的負荷トルクは主に摩擦トルクのことです。
回転系負荷トルク
T= 〔Ir x (モータギヤ/ワークギヤ)^2〕 x ω'
直動系負荷トルク
T= Ic x ω'
但し、Ic=Jc/gで、Jc=Mc x (A/2π)^2 です。
それぞれを求めてみましょう。
まずは、加速度によって生じる物体のイナーシャによる負荷トルク(Tr)を求めます。この時、回転系の負荷と直動系の負荷に分けて考えます。
回転運動系のイナーシャは、<モーターギヤ>になります。
直動運動系のイナーシャは、<ラックとワーク>になります。
回転運動系イナーシャIr (g・cm・s2) を求めます。
Ir=(GD^2/4)/g=Jr/g
ここで、Jr= Mr x K^2 = Mr x (r^2/2) (g・cm2)
但し、Mr:質量(モーターギヤの質量) (g) r:回転半径(モーターギヤの半径) (cm) g:重力加速度 980 (cm/s2) より、
Ir(従動ギヤ)=30x(3x3/2)/980=0.14 (g・cm・s2)
Ir(従動ギヤ)=0.14 (g・cm・s2)
Ir(モーターギヤ)=50x(5x5/2)/980=0.64 (g・cm・s2)
Ir(モーターギヤ)=0.64 (g・cm・s2)
直動運動系イナーシャIc (g・cm・s2) を求めます。
Ic=(GD^2/4)/g=Jc/g
ここで、直動運動する物体のイナーシャ(慣性モーメン)の式
Jc=Mc x (A/2π)^2 (g・cm2)
但し、Mc:質量(ラックとワークの質量) (g) g:重力加速度 980 (cm/s2)
A:単位移動量 (cm/rev)⇒単位:モーター1回転当たりの移動量(cm)より、
Ic=(40+600)x(8.3/2xπ)x(8.3/2xπ)/980=1.14 (g・cm・s2) Ic=1.14 (g・cm・s2)
よって、加速トルクTrは、
回転系(従動ギヤ)の加速トルク:
Tr= Ir x(モータギヤ/ワークギヤ)^2 x ω'=0.14 x (5/3)x(5/3) x ω'
【補足】
従動ギヤが対象で、モーターギヤは直結してるので、ギヤ比は1です。
回転系(モーターギヤ)の加速トルク:
Tr= Ir x ω'=0.64 x ω'
直動系の加速トルク:
Tr= Ic xω'=0.14xω'
但し、Ir :回転運動系 イナーシャ (g・cm・s2) Ic :直動運動系 イナーシャ (g・cm・s2) ω' :モーター 角加速度 (rad/s2)
ω'を求めます。
(最高)角加速度ω' (rad/s2)
基本駆動波形は、【図-9】のような基本台形波です。

まずは最高角速度ωを求めます。
回転角度は台形の面積となるので、
ω x (t1+t2)=θ x π/180 (rad/s)
但し、t1、t2はX軸の時間 (s) θは回転角度 (°)
ω=θxπ/(180x(t1+t2)) (rad/s)より、ω=720xπ/(180x(0.2+0.4))=20.93 (rad/s)
ここで、求める最高角加速度ω'は台形波の斜辺となります。
ω'=ω/t1=〔θxπ/180x(t1+t2)〕/t1 (rad/s2)より、
ω'=20.93/0.2=104.65 (rad/s^2)
よって、
回転系の加速トルク(従動ギヤ):
Tr=Ir x(モータギヤ/ワークギヤ)^2 x ω'=(0.14) x (5/3) x(5/3) x 104.65 =40.70 (g・cm)
回転系の加速トルク(モーターギヤ):
Tr=Ir x ω' =0.64 x 104.65 =66.98 (g・cm)
直動系の加速トルク:
Tr=Ic xω' =1.14x104.65=119.3 (g・cm)
回転系の加速トルク:
Tr=107.68 (g・cm)
次に外的負荷(バネや摩擦など)によって生じる物体の外的負荷トルク(=摩擦トルク)Tcを求めます。
直動運動する外的負荷トルク(摩擦トルク)の式
Tc=F x D/(2 x n x i) (g・cm)
水平の場合:F=Fa + μ x N
傾きがある場合:F=Fa + mg x (sinθ + μcosθ)
Fa:バネ力など、mg x sinθ 傾き方向の力、mg x cosθ 垂直方向の力
但し、F:直動運動方向の力 (gf) D:モーターギヤ直径 (cm) n:効率(0.85~0.95) i:減速比 Fa:外力(バネなど) (gf) μ:摺動面の摩擦係数(0.05) N:垂直方向荷重(=mg) (gf) m:ワークとラックの総質量 (g) g:重力加速度 980 (cm/s2) θ:傾き角度 (°)
では、まずはFを求めます。
垂直なので、F=Fa+μN のN(=垂直抗力)は、”0”になります。
ここで、Faを考えます。Faは、バネ力などの負荷になりますが、この場合、バネがないため、ワークとラックの総質量が、負荷になります。もちろん、バネがある場合、バネ力とワークとラックの総質量の総和が負荷になりますが、バネ力が負荷をかける側になるのか、または、負荷を助ける側になるのかを考慮する必要があります。本例題のようにバネ力がない場合は、
Fa= Fs + W = 40 + 600 = 640(gf) になります。
Fs:バネ力 W:負荷となる総質量
ここで、〔上り〕と〔下り〕でFaは異なることに注意します。
●〔上り〕の加速時は、"+"になります。⇒ (トルクを助けない方向<モーターに負荷をかける方向>)
●〔上り〕の減速時は、"-"になります。⇒ ((トルクを助ける方向<モーターに負荷をかける方向>)
●〔下り〕の加速時は、"-"になります。⇒ (トルクを助ける方向<モーターに負荷をかけない方向>)
●〔下り〕の減速時は、"+"になります。⇒ (トルクを助けない方向<モーターに負荷をかける方向>)
より、〔上り〕と〔下り〕に分けてそれぞれのFaを求めます。
モーターに負荷をかける方向:〔上りの加速時〕〔下りの減速時〕
Fa=+640(gf)
モーターの負荷を助ける方向:〔上りの減速時〕〔下りの加速時〕
Fa=-640(gf)
⇒モーターに最大負荷をかけるのは、〔上りの加速時〕
よって、直動運動する外的負荷トルク(摩擦トルク)は、
Tc=F x D/(2 x n x i) (g・cm)より、
Tc =640 x (3x2)/(2 x 0.95 x 5/3) =3,840/3.17 =1211.36(g・cm)
ここで、上述で計算した結果をまとめます。
回転系の加速トルク Tr=107.68 (g・cm)
直動系の加速トルク Tr=119.3 (g・cm)
外的(摩擦)負荷トルク(上り) Tc=1211.36(g・cm)
”上り”の加速時に発生する、モーター最大負荷トルクは、
T= Tr + Tc
Tr:回転&直動系の加速トルク、Tc:外的負荷トルク(=摩擦トルク)より、
T=(107.68+119.3)+1211.36=1438.34 (g・cm)
モーター最大負荷トルクT=1438.34(g・cm)
ちなみに、”下り”の減速時に発生する、モーター負荷トルクは、
T=(107.68+119.3)-1211.36=-984.38 (g・cm)
この場合の”-”は、下り方向の意味なので、
モーター負荷トルクT=984..38(g・cm)
つまり、”上りの加速時”が、モーターへの最大負荷が、かかる状態といえます。
次回は、直動と揺動の複合、ボールネジを用いた場合の負荷トルク計算をご紹介しようと思います。
よろしければサポートお願いします。 いただいたサポートは技術者としての活動費に使わせていただきます。
