QC検定1級過去問の解説(第37回の問1)
第37回過去問の解説まとめ
所感
2×2分割表における独立性の検定の問題です。期待度数と実現度数の考え方, 検定統計量の出し方が分かっていれば(1)〜(5)は正答できます。しかし(6)から知識がないと解けない問題になります。(6)は一応計算でも出せますがお勧めしません。式覚えた方が絶対に早いです。前半5問で5/8問正答したいです。
解説
(1)
求めるのは検定法の名称。A氏とB氏の評価に違いがあるかなので、独立性の検定。
(2),(3),(4)
求めるのは両氏の判定が1級品である確率の推定値, 2級品である確率の推定値, A氏が1級品と判定する期待度数。

(5)
求めるのは自由度。2×2の分割表なので、自由度は(2-1)•(2-1)=1。
(6)
求めるのは検定統計量。検定統計量は以下の関係が成立すると知られている。

(7)
求めるのはχ²分布と正規分布の検定統計量の関係。標準正規分布の検定統計量を2乗すると、自由度φ=1のχ²分布の検定統計量に等しくなる。以上より

(8)
求めるのはχ₀²の値。値を代入し
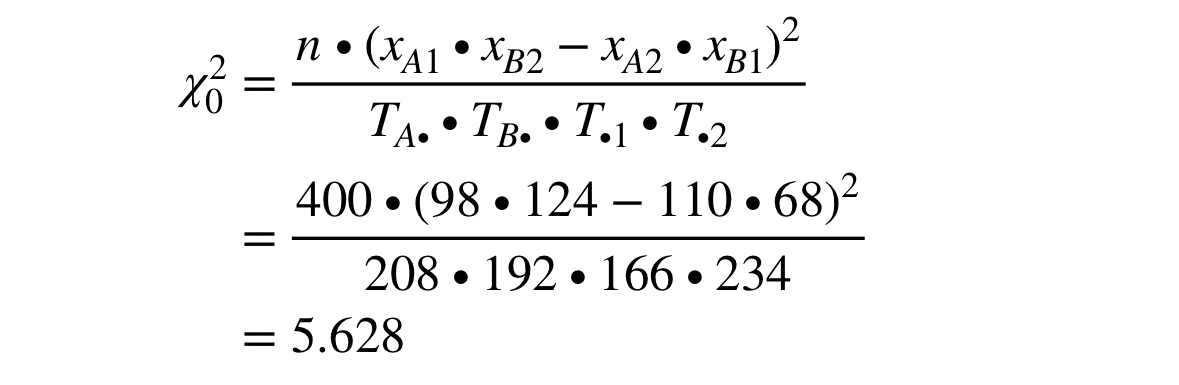
問題文が掲載されている書籍
Amazonのアソシエイトとして、このアカウントは適格販売により収入を得ています。
