QC検定1級過去問の解説(第36回の問1)
第36回マガジンのリンク
自己紹介
QC検定1級, 統計検定2級を持っています。現在は統計検定準1級の合格を目指しています。過去に合格したQC1級の復習として自分なりの解答を共有していこうと考えています。※解答のみで問題は載せません。
読者の皆さんからQC1級の合格者を増やし社会で活躍してもらいたいです。ひいてはQC1級仲間として僕も尊敬されたいです。次回の第39回で3630人目の合格者を目指しましょう！
所感
有限母集団からの2段サンプリングの問題です。平均値の分散の式が与えられていて、サンプリングの種類により適切に値を代入します。知っていればすぐに解ける問題です。8問完答したいです。この問題でサンプリングの種類と有限母集団からの非復元抽出はカバーできます。良問なので繰り返し解きたいです。
解説
(1)
求めるのは2段サンプリングの平均値の分散。問題文より
である。問題文の箱とびんで書き直すと
(2),(3)
求めるのは層別サンプリングの平均値の分散。層別サンプリングでは全ての箱からサンプリングをするため、M=mとなる。つまり、1項目が消えて
(4),(5)
求めるのは集落サンプリングの平均値の分散。集落サンプリングでは1箱の中の全てのびんをサンプリングをするため、N=nとなる。つまり、2項目が消えて
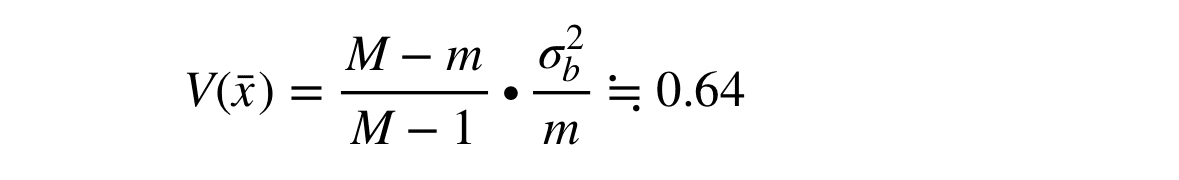
(6),(7)
求めるのは単純ランダムサンプリングのときのサンプル誤差の標準偏差, 平均値の分散。まず、標準偏差について分散を考える。箱内と箱間の分散は独立であるため、加法性が成立し
(8)
求めるのはどのサンプリングが1番精度が良いかである。全て計算すると層別サンプリングが平均値の分散が小さいため、精度が良い。
この問では
である。したがって、1箱の中の分散が項として消える層別サンプリングが平均値の分散が小さくなる。もし、上の不等式が逆なら集落サンプリングの方が良くなる。