＃80 バンクショットの持論と考察④（後編）

前回までのバンクショット記事・・・
※考察①#74はコチラ※
※考察②-前編#75はコチラ※
※考察②-後編#77はコチラ※
※考察③#78はコチラ※
※考察④-前編#79はコチラ※

★目次★

①バンクショットもクッション系、だから先球のスピードが合っていることが第一。

②先球に生じるスピン（特に横回転）の影響を考慮する必要がある。そしてスピンを活用すれば色々な狙いができる。

③バンクにもシステムがあるが、システムに乗せるためにはシステムに合った撞き方が必要。

④鋭角（クッションに対してより垂直に近い）のバンクと、鈍角（クッションに対してより平行に近い）のバンクにおける、スピンやクッション反発の影響の差とは。

⑤縦バンクは何故難しいのか？鋭角と鈍角のバンクは？それは数学的に明らかである。

⑥ショット後の手球がイメージできない・手球コントロールを伴わないバンクショットを撞くのはちょい勿体ない。

⑦手球コントロールという要素を考えると、時に直接ポケットよりバンクショットの方がイージーになる場面が存在する。

今回は目次の④の後編・・・

ここからは今回の本題「鋭角なバンクと鈍角なバンク」についての考察

の前にちょっと余談・・・
先日「バンクシステム」の記事（#78の考察③）の中で、「システムは反射角の詰まり想定」的な事と「クッションが詰まる理由」について書きましたが、前編で示した一例が正にこの話の部分になっています。
要するに、ビリヤードにおける基本的な「クッションの特性」は、反発吸収より摩擦相殺が勝っている「詰まる」状態ということなのでしょう。

図１：考察③で紹介した「バンクシステム」
入射角（青線）に対して反射角（赤線）はクッション垂直方向に詰まる想定で数値設定されている

図２：考察④前編で示した「クッションによる反射角の変化の一例」
この一例は「垂直方向の減衰率が小さく、水平方向の減衰が大きい（クッションの反発吸収より摩擦力がより影響を与えている）」ことにより、反射角が入射角より詰まるパターンを示している。

改めてここから本題・・・

次の図である
クッションに垂直な方向からある一定のスピードと回転でショットした時に、反射角が開くことは多くのプレーヤーは理解していると思う（黒線→黒点線の球の動きのイメージ）。では鋭角な入射角の場合や鈍角な入射角の場合には反射角の開きはどうなるのでしょうか。

図３：クッションに垂直な方向からある一定のスピードと回転でショットした場合（黒線の球）、反射によって開く角度があるとする（黒点線の球）。では同じショットにより鋭角な入射角の場合（桃線の球）と鈍角な入射角の場合にも開く角度は一定なのか？

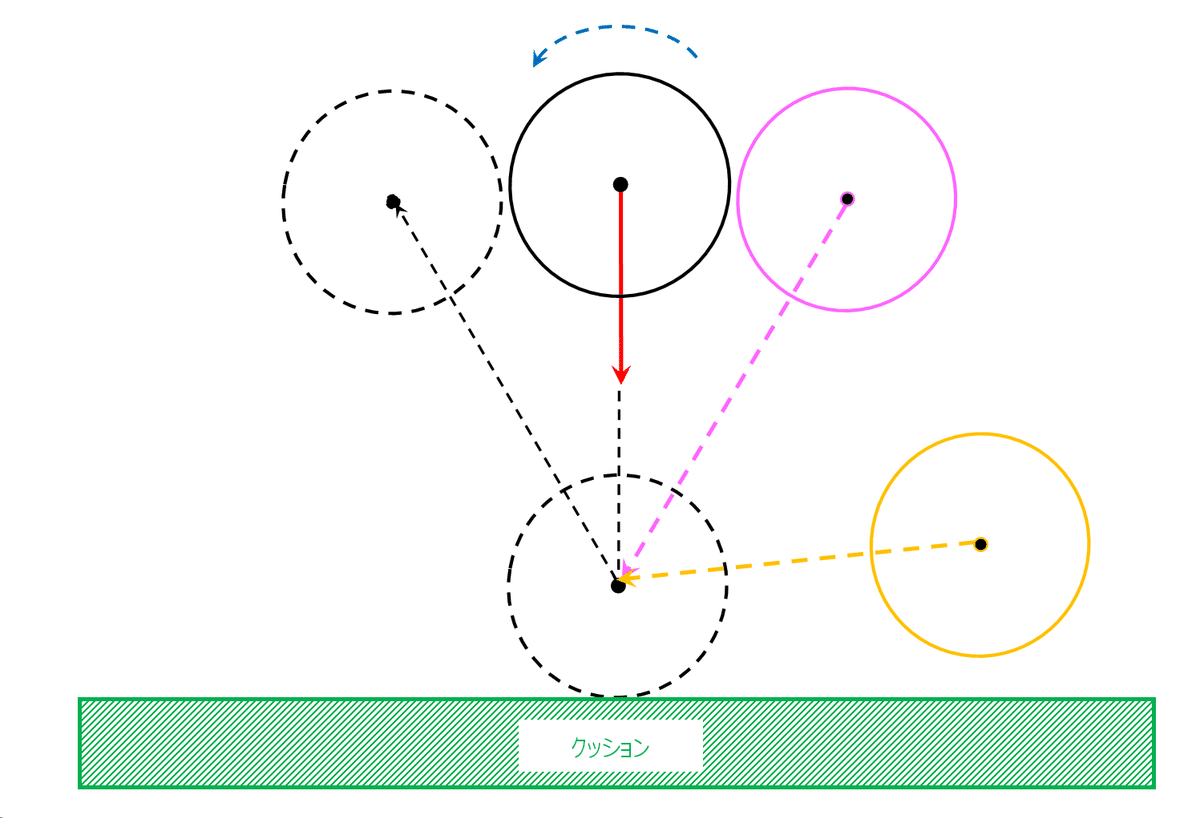
垂直に向かった場合と同じ反射角の開き方をするのかというと、どうも同じでは無い事に気が付くのではないだろうか。

図４：桃球は黒球と同じ様に反射角が開きそうにも思えるが、では橙球が同じだけ反射角が開いたとしたら？？？

ここで前編で述べた「クッションの反射についての物理的考察」を思い出してほしい。
斜めに進む力は垂直と水平の成分に分解できる。
今回は順ひねり想定なので水平方向の成分が増大する。
鈍角な反射角になるほど垂直方向の成分は限りなく小さくなっていく。もしも垂直成分＝０であったならば（クッションを這う球　通称「ゴキ〇リ」のイメージ）、水平成分がどの大きさであったとしてもそれはクッション面と平行に這っていく球にしかならないはずだ。

まとめ直すと、
・「クッションと垂直な成分：水平な成分→垂直な成分が比率的に大」である・・・水平な成分の変化量による角度の変化も大きくなる
・「クッションと垂直な成分：水平な成分→垂直な成分が比率的に小」である・・・水平な成分の変化量による角度の変化は小さくなる
これは順ひねりだろうが逆ひねりだろうが、ラシャの摩擦相殺だろうが同じである。
※ただし、ひねり（回転）が与える力の影響は、球自体の移動する力とは異なる外力的な働きをしているとも考えられる。よって純粋な球の移動する力と分解した成分にのみ影響を受ける摩擦相殺での角度変化については
・「水平方向＝０（バンキング系）」ならば垂直方向に集束
・「垂直方向＝０（クッションレールに沿って走る）」ならば水平方向に集束
と考えて間違いないはずである。

図５：鋭角な反射（桃線）では垂直な反射に近くなるが、鈍角な反射では開きがほとんど無い。
※垂直方向の反射の減衰と水平方向の摩擦相殺は無いものとする

更にこれを数学的にも考えてみよう！

図６：垂直成分（赤線）と水平成分（青線）で作られる入射角θおよび反射角θ’が存在する
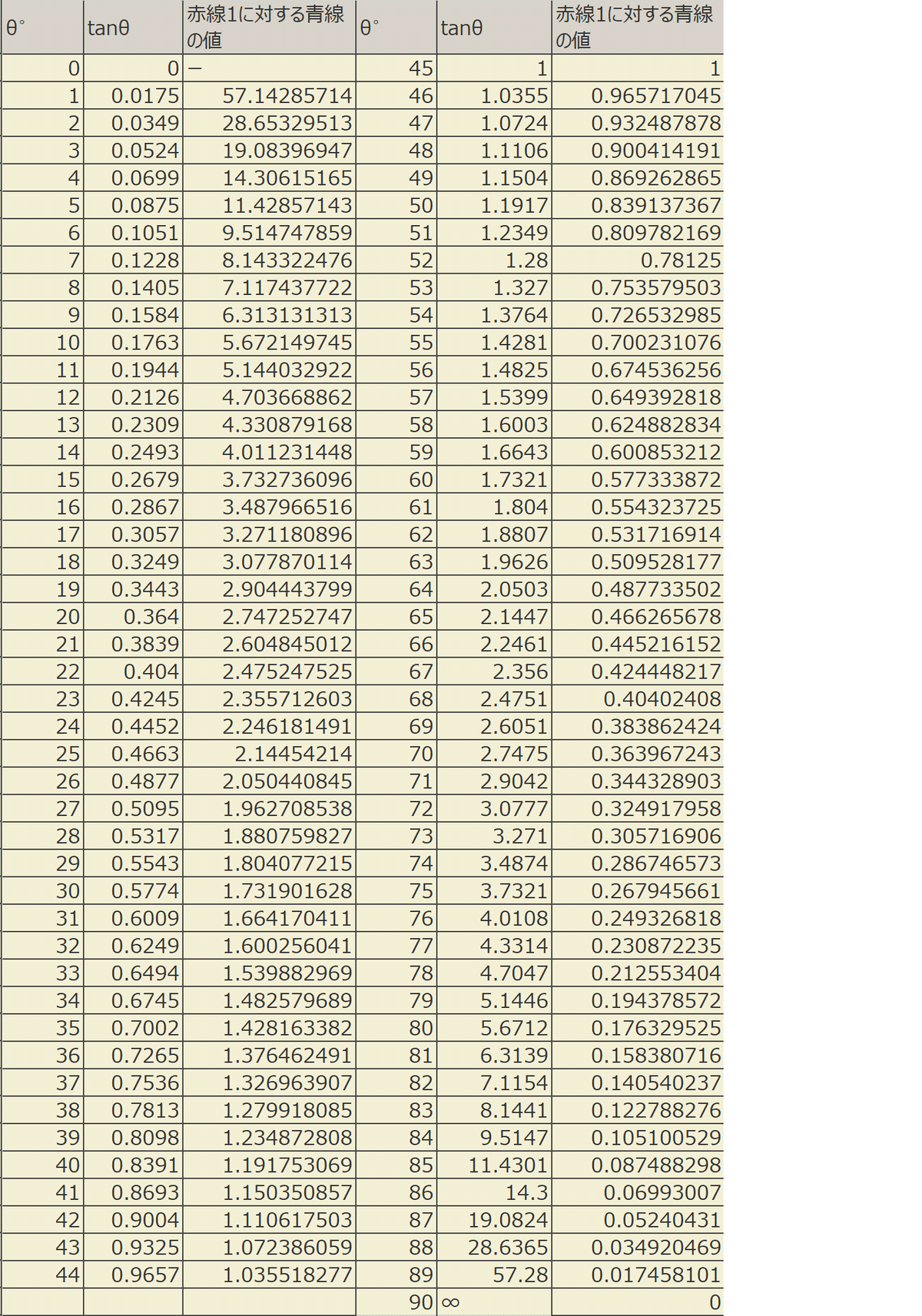
赤線／青線により「tanθ」が求められる。

図は入射角と反射角を図形（直角三角形）のイメージで描いたものである。
ある入射角θとその垂直成分・水平成分が存在した時、反射により「垂直成分は固定」「水平成分は一定の変化」が発生した場合に反射角θ’はどれだけ変化するか？というものである。

まずθ＝90°（クッションに対して垂直に撞く）の場合、水平成分＝０である。（水平成分の値は表の「赤線1に対する青線の値」である）
・水平成分：０→0.5増えたとして表を見ると　※要するに0.5増える順ひねりと想像してほしい
θ’＝約63°（クッションに対して垂直のラインから約27°変化）
・更に0.5→1へ増えると　※この辺が鋭角のクッションのイメージ
θ’＝45°（垂直のラインから45°　27°→45°で18°変化）
・更に1.0→1.5へ増えると
θ'＝約33°（垂直のラインから57°　45°→57°で12°の変化）
・更に1.5→2.0へ増えると　※この辺から鈍角なクッションのイメージ
θ’＝約26°（垂直のラインから64°　57°→64°で7°の変化）
・更に2.0→2.5へ増えると　※かなり長いクッションのイメージ
θ’＝約22°（垂直のラインから68°　64°→68°で4°の変化）
・最後にθ＝3°（垂直のラインから87°　青線の値約19）に対して
19→19.5を見ると・・・
θ'＝2°・・・にすら変化しない（同じひねりでも１°変えられない）ことが分かるはずだ！

図７：三角関数（tanθ）

最後にクッション反発の差が与える影響とは・・・
ここまで読んでくれた皆さんならもう何となく予測できているかと思われるが・・・
反発係数が小さい（クッションが勢いを殺す）と、跳ね返りの垂直成分が水平成分に対して比率が小さくなる。よってより水平成分の変化による角度変化の影響も大きくなる。
「捻りが噛みやすく伸びるクッション」というのは概ねこのようなコンディションを言うのだと考えられる。

④の考察は以上になります。←バンクショットというよりクッションの考察になった感じで・・・