Bombeとかいうゲームについての手記
このnoteは私が淡々と頭の中を整理するために書くnoteです。
過度な期待はしないでください。
前フリはそのくらいにしまして、Bombeとか言うゲームの話をします。
このゲームがどういうゲームなのかについてはZubuさんの記事であるBombe攻略メモ(上級編)及びZubuさんの投稿している動画シリーズ【Bombe】ずんだもんにマインスイーパーを自動化してもらうを御覧ください。
ZubuさんはPatashuのGuideなどを参照することを勧めていますが、今回私がこの記事で書くのはBombe Demoという体験版の方になります。
Bombe Demoについて
このBombe Demoは本編であるBombeからヘキサゴンのうち2000問、スクエアのうち2000問を抜き出したゲームです。具体的には……

こんな感じで2000問だけでてます。本編をすでにプレイしていたり、上述のZubuさんの動画を見た方はお気づきかもしれません。そうです。Demo版は完全クリアするまでXが使えないのです。(+-や!などは使えます)
なので全てのルールはいちいち個別にルール設定する必要があります。

さて、このようにすごくすごい環境下で解かねばならないわけですが、じつはSteam実績は結構すごいことになってます。

嘘……5%もクリアしてるの……!?
これは本編で言うところのトライアングル5000問正解実績と(だいたい)同じくらいです。

さて、ここまで長々と語りましたがつまり当noteでは『なんとかDemo版くらいはクリアしたい!』というところに焦点を当てた記事です。なるべく、Demo版クリアまでに設定すべきルールを示せればと思います。
なお、以下から爆弾◯個を含む✕マスを◯:✕と表記し、それを情報指定と呼びます。
1. 基本のルール
まずは誰でも思いつく簡単な基本のルールです。いくつか示します。

マス数指定が?になっていることについては解説は不要でしょうが、一応書いておきます。爆弾の数がある範囲で0と言われた場合、その範囲がどのようなものであっても開いて良いということです。

こちらも同じように、例えばあるマス一つだけを含むの範囲について、爆弾が一つ含まれているという情報が得られた場合、そのマスは爆弾に確定します。
ここで補足しなければならないのは、マスの範囲指定にマイナスがついている(つけられてしまう)ことです。
実際には1:0の盤面というのは存在しません。ですから、このルールは矛盾を抱えていそうですが成り立ちます。Bombe側で受け付けないルールは基本的にロジックエラーか重複しかありません。たとえば下記は受け付けないルールです。



なお、マウスオーバーすると反例を示してくれることも合わせて覚えておくべきでしょう。
なお、ここでルールについて少しだけ追加解説をします。
情報指定について、◯:✕という情報が示された場合、◯+:✕というルールは適用されません。文字で書くとどうにも分かりづらいですが、例えばこんな例です。

上記画像の情報指定1:1について、爆弾であることは自明です。ここでルール指定をします。

『1以上の爆弾を含む範囲が1マス以下の場合、そのマスは爆弾である』という文章はどうしようもなく正しいはずですし、このルールはまさにそのように書かれています。そして1マスの範囲について1つ爆弾があるというのは1+と1-の指定された範囲に収まっています。しかし実際にはこれは動作しません。なぜならば、
Bombeというゲームは◯:✕という情報指定について◯は完全一致でルール適用し、✕は意味を解釈してマス数が合致するかどうかを考えているからです。ですから実際にはわざわざ1:1-と1+:1-というルールを作らなくてはなりません。
というのも半分嘘で、実際は下記のルールを足すべきです。

このルールが概念拡張です。つまり1+:?という情報指定は常に1:?を含んでいるということです。そして今回のルールに限って言えば、1:1-と1+:1-は情報的に等価(ルール適用して開ける範囲が変わらない(※1))です。
※1 等価であることの証明
情報指定1+:1-を得た時、最大でも爆弾の数は1-である。そのため、
情報指定1+:1-の範囲について同時に1-:1- である。範囲yがx+:yかつx-:yであるときx:yである。(※2)
そのため情報指定1+:1- = 1:1-である。
※2

さらに補足すると、範囲yがx:yであるとき、x+:yかつx-:yです。


ここまでの話をまとめると、ルールについては広い範囲の指定(1よりも1+など)が良いということになります。そのためにはまず狭い範囲の情報をより広い情報へ(情報が欠落してもまずは)拡張する(つまり概念拡張する)、そして広い範囲のルールでまずは情報を洗い出し、その後概念を厳密にしたあとに細かなルールで対応するという流れになるでしょう。
概念拡張→汎化ロジック→概念縮小→専用ロジック
なお一番広い爆弾数指定は+もしくは-の形になりますので、概念拡張はそこを目指すことになります。(1から1+2*などには直さなくてよいです)
逆に概念縮小は1などの一番具体的な数を目指すことになります。
2. 概念拡張
さて、それでは以降に概念拡張のルールを示します。まずは先んじて示した『1:?は1+:?を常に含む』、『1:?は1-:?を常に含む』。画像略。
次に選択系の爆弾数の場合も+の形へ直せます。

奇数系も+の形へ直せます。

選択系も-もしくは+へ直せます。


否定形はその殆どが0+にしか直せず、汎用ロジックはなかなか使い難いです。
また、+を更に大きな+要素で拡大することもできます。

同様に-にも適用可能です。

さて拡張しまくったわけですが、上記のように拡張するとどうなるでしょうか?答えはこの通り。

本当は無限の選択肢からピタッと規則性を発見できればいいのですが、それもなかなか難しいので、下記のようなルールで表示制限をかけます。

片方の領域がもう片方の領域に内包されていれば小さい方を表示しない
なお、チェックマークが黄色くなっている場合は非表示にしないほうが良いです。こちらもマウスオーバーすれば理由がでますが、情報量が失われているためです。実例も一緒に示されますがちょっとだけわかりにくいです。
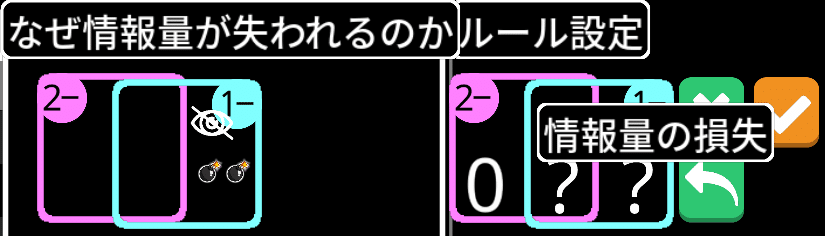
この状態で1-:?を非表示にすると、『1-側の領域に2個の爆弾はない』という情報が
盤面から失われる。
3. 汎用ロジック
主に+や-で利用でき、確定できるロジックです。
ここまでで概念拡張により少なくとも正しい理屈を示せば、その理屈の下に盤面に反映するための材料は用意できました。
基本ルールで示した『1以上の爆弾を含む範囲が1マス以下の場合、そのマスは爆弾である』もこれに当たります。

またこんなものもあります。『1-:?と2+:?が重なっており、2+側のみに入るマスが1つ以下であるとき、1-側のみに存在するマスはすべて爆弾ではない』

1-側のみに存在するマスはすべて爆弾ではない』
※証明
1-:?の範囲には1個または0個のみ爆弾が入る。2+:?側には2個爆弾が入るが、その内訳は必ず『1-側と被っている範囲に一つ入り、被っていない範囲に1つ入る』しかない。なぜならば、1-側の範囲に2個爆弾が入ることはなく、1つしかないマスに2個以上の爆弾は入らないため。
内訳が上記であるため、1-側にのみ存在するマスはすべて爆弾ではない。(重なり合う範囲に爆弾が1個存在するため)
また同様に2+側にのみ存在するマスは爆弾で確定である。
その他色々ありますが長くなるのでここらへんで……
4. 概念縮小
今度は逆に概念を縮小していきます。縮小したほうが情報が詰まっているため爆弾箇所の特定が容易です。私的にいちばん有名なのは以下でしょうか。

『1-:?と1+:?の範囲が被っている時、その範囲は1:?である』
1以下と1以上の範囲が被っている時、当然にその範囲は1ぴったりでなければなりません。1+と1-という広い範囲が2つあるだけで、その範囲内の爆弾が1個に確定します。
また下記のようなものもまあまあ使えます。

1:?の範囲に含まれていない2:?の範囲は1:?である
『1:?の範囲が2:?の範囲に内包されている場合、1:?の範囲に含まれていない2:?の範囲は1:?である』
この1:?の範囲に1つだけ爆弾が存在する以上、2:?でその範囲以外に1つ爆弾があると確定せざるを得ません。伝わりますでしょうか。
余談ですが、Xの存在する本編では存在しない問題が体験版には存在します。どれだけたくさんルール作ればいいかわからない問題です。
上記のルールの類似系として例えば下記があります。

2:?の範囲に含まれていない3:?の範囲は1:?である
『2:?の範囲が3:?の範囲に内包されている場合、2:?の範囲に含まれていない3:?の範囲は1:?である』
こちらも先程のものと内容は同じです。しかしルール適用の都合上別途このルールも設定する必要があります。このルールは左側の範囲の爆弾数と右側のルールの爆弾数の差が1つであるときに成り立ちます。これは本編ではxやらψが使える本編では一つのルールで網羅できますが、体験版ではすべて手動で定義する必要があります。1と2、2と3、3と4……と作っていったときにふと気づくでしょう。
「差が2のときは別な法則が成り立つのでは?」

1:?の範囲に含まれていない3:?の範囲は2:?である
『1:?の範囲が3:?の範囲に内包されている場合、1:?の範囲に含まれていない3:?の範囲は2:?である』
当然成り立ちます。ということは差が3の時、4の時……と続くわけです。ということで全部作ってみた結果が次の通りです。



長い……。ということで実際作ってみましたが、ほとんど使うものは同じようなものばかりです。差が4の組み合わせなんて使ってません。xも使えないのですから、汎用化は程々にしておきましょう。
5. 専用ロジック
ここが問題を解き切るときの要です。要はそれぞれの形でしか使えない独自のルールです。例えばチュートリアルにでてくる物が有名でしょう。


1:?が3つ重なっており、うち一つの1:?がその他二つの1:?に内包されている時、
内包されている1:?に含まれない二つは1:?の関係にある
『1:?が3つ重なっており、うち一つの1:?がその他二つの1:?に内包されている時、内包されている1:?に含まれない二つは1:?の関係にある』
さてこれはなぜでしょうか。
まず仮定してみましょう。

aに爆弾が含まれている場合
aに爆弾が含まれている場合、まずcに爆弾は入りません。cに入らない以上、dには必ず爆弾が入ります。同様にbにも爆弾は入りません。そのため、下図1.のような爆弾関係になります。cに爆弾が含まれている場合
cに爆弾が含まれている場合、同様にaは爆弾が入りません。同様にdにも爆弾が入らず、自ずとbに爆弾が入ることになります。そのため、下図2.のような爆弾関係になります。


さて、上記の2パターンしかないということが明らかです。(それ以外では矛盾が生じます)その場合にどのようなことが言えるでしょうか?
aとbに合計で1つ爆弾が入る。
aとdには0/2:?の関係である。
bとcには0/2:?の関係である。(上記と同じ)
このくらいです。簡単ですね。では2へと進みます。

先に答えを示しますが、この法則はそれぞれが2であっても成り立ちます。
この問題のパターン理由は1のときと違ってかなり増えます。
aにだけ爆弾が含まれている場合
cにだけ爆弾が含まれている場合
aとcに爆弾が一つづつ含まれている場合
それぞれについて考察していきます。
まずaにだけ爆弾が含まれている場合、cに爆弾が入りません。よってdに爆弾が2個含まれます。dに爆弾が2個ある以上、bには爆弾が入りません。
次にcにだけ爆弾が含まれている場合ですが、上記と同じように考えれば1のときと同じようにbとcにそれぞれ爆弾が2個入ります。
そして最後にaとcに一つづつ含まれている場合、dには1個爆弾が入ります。そしてbにも爆弾が1つ入ります。なのでそれぞれの領域に1個づつ爆弾が含まれます。
さて、これでパターンは考察し終えましたが、ここから何が言えるでしょうか?
aとbには2つ以上爆弾が入る。
aとdには0/2/4:?の関係である。
bとcには0/2/4:?の関係である。(上記と同じ)
3の場合も同様です。しかし0/2/4/6という表現は存在しないので2*という表現になります。そして成り立ちはしますが体験版の範囲内では使いません。

こういうパターンは文字を使わないと特に指数関数的にパターン数が増えていきます。文字さえ使えればBombeの判定任せにできるので非常に簡単になりますが……。もうひとつだけ別パターンの検討をします。最後は3:?,3:?,2:?のパターンです。

考えなければならないのは6パターンで、defにそれぞれ下記の通りに爆弾が入るパターンです。

パターン1の場合、aとbの範囲に1個爆弾が入る。aに爆弾が入る場合はcは爆弾が2個でbに爆弾が入るときはcに爆弾が1個。つまりパターン1の場合は下記の通りの配置になる。

パターン2の場合はパターン1と鏡写しなのでほぼ同様。
パターン3の場合もaを中心に考える。aに入る爆弾は0個または1個または2個。0個の場合はbに2個入る。これはc側も同じなので、aとcには同様の個数が入る。

パターン4の場合、パターン1と同様にaとbの範囲に1個爆弾が入る。異なるのはcに入る爆弾の数で、それぞれaに爆弾が入ったときは3個、bに爆弾が入ったときは2個。

パターン5もパターン2と同様に鏡写しなのでカット。
パターン6の場合もやはりパターン1と同様にaとbの範囲に1個爆弾が入る。
結局まとめると下記の図の通りになる。

つまり……何もわかりません!強いて言うならばbが0の時、aは1/2/3になるが、あまり情報が増えているとは言い難いでしょう。
ここまでの情報ではたしてDemo版のすべてを解き明かせたでしょうか?
おそらく無理だと思います。(時間をかければできるかもしれません。)
では一体なぜ、この実績解除率は5%前後もあるのでしょうか。難易度とかける時間に見合わなすぎるのでは?そう思うでしょう。
答えはこれです。

そう、合法的にチートができるのです。製品版ならね。
この状態であれば、『2000問をクリアする』という実績解除条件が全く変わってきます。この実績は『(製品版を含めて)2000問をクリアする』という実績解除条件なのです。つまりこの状態でもすでに全実績解除です。Pay to Winというやつですな。ガハハ。
はい、ということで次回は真面目に製品版の攻略を書きます。
Demo版の実績解除は製品版を買ったほうが楽です。Xが使えないのがいくらなんでもしんどすぎる。
