Bombeとかいうゲームについての手記 その3
このnoteは私が淡々と頭の中を整理するために書くnoteです。
過度な期待はしないでください。
さて、ではその3では実際にルールを紹介及び検討していきたいと思います。
ここまでの話をまとめると、ルールについては広い範囲の指定(1よりも1+など)が良いということになります。そのためにはまず狭い範囲の情報をより広い情報へ(情報が欠落してもまずは)拡張する(つまり概念拡張する)、そして広い範囲のルールでまずは情報を洗い出し、その後概念を厳密にしたあとに細かなルールで対応するという流れになるでしょう。
概念拡張→汎化ロジック→概念縮小→専用ロジック
1. 概念拡張について
まずは概念拡張から。
その1で書いたように、概念拡張はその情報はどの情報を内包しているかを示すためのルールです。
例えば情報指定χ:?において、その範囲にはχ+であることが確定しています。
もっと具体的に言うと、とある範囲にχ個の爆弾があるという情報は、χ個以上の爆弾が入っているとも言い換えることができるということです。

私が現状使っているものをそのままコピペしたものが下記です。
Bombe Rules (22):
💣⠨⢵⠯⣽⡣⡂⣯⠺⠅⣃⠋⠥⠆⠀⢒⣄⠐⠘⢐⢵⡭⡨⢕⢆⢲⣊⠣⡖⢸⡂⣿⠙⣝⠢⢻⣛⠍⡮⣆⢻⣋⠳⢅⠂⢡⣙⣧⣡⠫⠺⠳⡞⡓⠋⡫⣉⢛⣽⣢⢏⢦⠒⣩⠆⢂⣕⡬⣵⣓⠝⠪⣐⠌⣀⠍⣙⡘⠣
⣈⢫⠪⡩⡽⢄⠯⢸⡀⢅⣖⠰⢍⠁⢑⠘⡡⡅⡘⠑⠔⣡⢏⠅⡅⢘⠙⣨⠃⡻⣙⡿⡁⡞⡁⢺⣋⢁⣤⡐⡰⠒⣿⢊⣞⢔⣜⣾⠜⣂⡴⣱⡼⢘⠵⢅⡜⣦⢅⡻⢛⣗⣃⡹⢈⡯⢂⢃⢙⣼⠗⣳⠕⣾⠟⡢⡴⣙⡲⣮
⢣⡑⡔⡿⡯⡳⣒⠇⡘⠛⠑⢻⢙⠻⡠⣦⣁⡂⢩⡚⣪⡰⢬⡸⢩⠊⡮⠭⢥⢗⠾⢌⢥⢶⣗⠫⡍⣄⢲⠴⠸⡇⣔⠦⣂⣝⢣⣟⡯⠄⣂⠎🛑
さて、この中に含まれていないものとして下記のようなものがあります。

このルールがどうこうという話はここではしませんが、これも『自明の範囲からより広い他の情報が導出される』という意味では概念拡張の一種と言えます。ですが、ここでは概念拡張を狭義の意味で使用します。
狭義の概念拡張:そのルール自身が持つ意味をより広いルールへ置き換えるルール
狭義の概念縮小:そのルールたちが持つ意味から、より狭い範囲についてルール定義をするルール
上記の通りに解釈すれば、このルールは概念縮小に当たります。
先ほどコピペしたルールたちは、すべてこの狭義の概念拡張に該当するものです。一つ一つ見ていきたいと思います。

『χ:?は常にχ+の意味を含む』。これは素直にその通りです。また、χ-も同様に含まれます。

『χ:?は常にχ/χ+1の意味を含む』。これもやはりその通りです。他にχ/χ+2やχ/χ+1/χ+2なども含みます。

『χ/χ+1は常に(χ+1)-の意味を含む』。これもその通りです。他にもにχ/χ+2やχ/χ+1/χ+2なども同様のことが言える他、『χ/χ+1は常にχ+を含む』とも言えます。

『(χ+2)+2*:?は常にχ+2*の意味を含む』。ぱっと見て意味がわからないかもしれませんがこれは正しいです。具体的にχに代入してみればそれは明らかでしょう。χ=0を代入してみましょう。
証明
χ=0のとき、上記のルールは『2+2*:?は常に2*を含む』となる。これは常に成り立つ。何故ならば、2+2*が示す爆弾の個数は2,4,6,8,……の偶数個であるのに対して、2*が示す爆弾の個数は0,2,4,6,8,……の偶数個、つまり0/2+2*と示すことができる。そのため、上記は常に成り立つ。
これは一般化した後の式である『(χ+2)+2*:?は常にχ+2*の意味を含む』についても成り立つ。つまり『χ+2*の示す爆弾の個数はχ/(χ+2)+2*』である。
更にもう一つ偶奇関係について。

『χ+2*は常にχ+の意味を含む』。こちらは解説は不要でしょう。
先程と同様に考えればχ+2*はχ,χ+2,χ+4,……と続くので、これはつまりχ+に含まれる範囲です。

また偶数のみが選択肢に上がっている場合は2*としても良いというルールもあります。上記のルールは先程挙げた一覧にはないものですが、これは2つのルールによって成り立っています。

『χは常にχ+2*の意味を含む』。これももちろん成り立ちます。
例えば2は常に2+2*の意味を含みます。これが1つ目のルールで、もう一つが先ほど紹介した『(χ+2)+2*:?は常にχ+2*の意味を含む』というルールです。これにより、例えば2のとき、
『2は常に2+2*の意味を含み、2+2*:?は常に2*の意味を含む。つまり2は常に2*の意味を含む』ということになります。これにより、例えば下記のようなものも成り立ちます。


さて、ここまでで概念拡張についてざっくりとご紹介しました。
汎化ロジックもご紹介したいのですがまだまだ汎化できているか怪しいものもたくさんあります。検討の過程を示すのも大事だと思いますので、まずはチュートリアルにて示された問題から汎用的にしていきたいと思います。
2. チュートリアルにて示されたルールとその汎化

チュートリアルの答えは下記です。

『1:2と1:2の範囲が被っておらず、かつ両者にまたがる1:2が存在する時、またがる1:2に含まれない部分について1:2の関係が存在する』。
と、日本語でそのまま書くとこうなるのですが、非常に分かりづらいのでチュートリアルの画像を見ながら赤い線も1なのだと思ってください。
ではこれが何故成り立つのか。それを考えていきます。
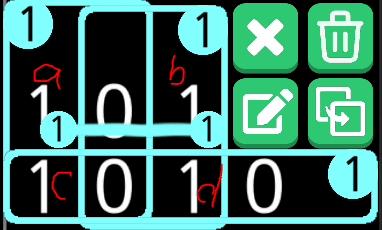
なんと、この盤面ではaのみを考えればすべてのパターンが洗い出せます。
全ての爆弾の個数のパターンは以下の通り。

証明
aに爆弾が入る時、cに爆弾は入らない。cに爆弾が入らない場合、dは爆弾で確定するため、bに爆弾は入らない。
aに爆弾が入らない時、cに爆弾が入る。cに爆弾が入る場合、dは爆弾が入らないため、bに爆弾が確定する。
よって上記表の通りに爆弾の内訳が確定し、a-b間には常に1個爆弾が入る。
さて、ここまでは良いのではないでしょうか。
先にこのゲームのルール設定について少しだけ書きます。
A&!Aと表記されている場合、そのルールは現実的に起こり得ないため設定不可能となります。例えば下記のようなルールです。

2:?だけ見るとすべてのマスが爆弾で確定しているはずですが、そうすると1:?に爆弾が2つ含まれてしまいます。つまりこの盤面の設定自体が論理的に矛盾しています。前提が成り立っていません。そのため不可能となります。
ではこの2をχに変えるとどうなるでしょうか?

不可能ではなくなります。
これはつまり、χに代入される値は0以上のすべての整数で間違いないのですが、そのうち不可能となるルールについては検討せず、検討しないもの以外を適用する、ということです。つまりこの場合のχは0または1のみルールとして適用されます。
さて、少し盤面を変えてみましょう。

この場合はa-bの関係性は2です。
表に表すと下記の通りです。

aが0個の場合はありえません。何故ならば2:2の範囲はすべて爆弾で確定するためです。
さてもう少し盤面を変えてみましょう。

3:2というのはありえないので、一部マスの数を増やしています。
これもやはりa-bの関係性は3になります。

4以降も試してもよいのですが、ここらへんで一般化してみましょう。
少なくとも前述したように置き換えた部分は変数にできそうです。
3からχへ置き換えました。すると見出される回答もやはりχになります。
それぞれのマス目は関係なくあくまで爆弾の個数だけで推論は成り立ちましたから、それぞれの1としたマス目は任意のマス目で成り立つはずです。実際にルールが成り立つことを確認して終了。……としてもよいのですが。
「まってよ!ほかの1:?が変数化できそうだよ!」と声が聞こえてきそうです。もう少し考えてみましょう。まずはこのルールの個数はどのように確定しているかです。

爆弾の個数内訳はこの通りになります。先ほどと同じ考え方でaの個数を確定させるとc,dが確定し、残ったbも確定します。
χ個の関係性にあるのはa-bはたしかにそうですが、b-dも同様の関係性にあります。(b,dはもともとχ:?に含まれる範囲なので当たり前ですが)
また、a-dについては0/2の関係を持ちます。
そしてa-cについてはχ-1/χ+1の関係があります。次数を一つ上げればこれも表現でき、下記の通りになります。

ではここから左上の爆弾の個数を変化させます。


aが0である場合は存在しません。(不可能)
aは2または1になります。しかしどちらの場合であってもうやはりcとdが確定し、bが求まります。主な関係性はおそらく下記3つでしょうか。

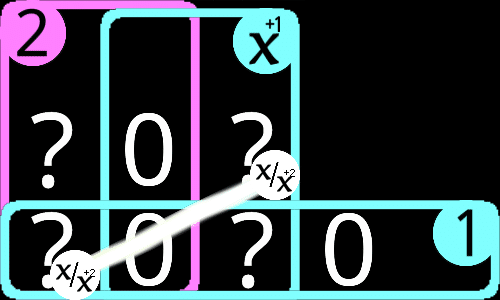

その中では特に最後のもの、つまりa-b間の関係がおそらく特筆すべき点でしょう。左上が1であったときと比べてちょうど1だけ高くなっています。ということは……?

おそらくこういった関係が成り立つでしょう。というか成り立ちます。
ここでちょっと本筋からそれますが、次数を上げた理由(ψ+1になっている)について説明します。先程の表ではa-b間の関係は常にχ+1となっていました。しかしここでaをψとした場合、a-b間の関係は常にχ+ψ-1となります。
これはχ+ψが0以上になる場合は問題ないのですが、χ=0,ψ=0などの場合に問題になります。(両者の関係性で、爆弾の個数が-1個というのはありえない)もちろんχ+ψ-などに設定すればルールとしては成り立ちますが、個数を確定させるロジックのほうがおそらく都合が良いでしょう。
さて、ここまでで2つの文字でルールを定義することができました。
しかし文字が2つ以上になると問題が起きます。非常に個数内訳が書きにくいのです。とはいえ今回のパターンは大丈夫そうです。何故ならば下記の通りになるからです。

ここで重要になるのは爆弾が1である範囲が存在していることです。
この1という制約によってほとんど全部のパターンは不可能になります。よって、結局aにはψまたはψ+1しかありえません。その場合は結局先程示した内訳と同内容になるので、結局bの個数まで確定します。
変わるのは文字となったψとχの和の数が爆弾の個数になるというだけです。
さて、まだあと一息です。もう一息頑張って、右下の個数を変化させましょう。

さて、こうである場合に、やはり同様に個数内訳を考えます。先ほど示した例では、結局ψが増えてもパターンは2つでした。この場合は何パターンあるでしょうか。

上記の通りです。ここで気にして欲しいのは、パターン数が増えているということです。つまり、爆弾の個数内訳における不可能ではないパターンの数というのは、要は右下の個数を2つのマスに振り分ける組み合わせの数になります。具体的には片方の爆弾の個数を確定させればもう片方は確定しますので、この場合は0,1,2の3パターン。右下を仮にκとすれば、(κ+1)C1となるでしょう。(CはcombinationのCです)
表より、例えばこんな関係性が成り立ちます。


このうち、前者はこのままの形式では一般化できなさそうだとわかりますでしょうか?
前者は確かに右下が2のときは成り立ちますが、3の場合はχ/χ+2/χ+4/χ+6となるからです。(正確に言えばχ-2/χ/χ+2/χ+4)
ただ、後者は一般化できそうです。もう少し続けてみましょう。


こちらもやはりa-b間の関係性は常にχ+ψ-1になります。-1になってはいけないので、χに1を足せば何らかの関係を示せそうです。
またa-c間の関係も同様ですが、こちらはχに2を足さなければ一般化できなさそうです。


さて、ここからκを利用できることに気がつけますでしょうか。
先に爆弾の個数内訳を考えてみます。
それぞれの爆弾の個数をψ+1,χ+1,κとしたときのそれぞれの内訳です。

ここで困ったことに気づくでしょう。a-bを足しても一般化できないのです。例えば表の下の方だけ見てa-b間の関係をψ+1になるとします。しかし……

このように非論理的だと判例を示されます。まさにぐうの音も出ません。これまでと一体何が違うのでしょうか?答えは爆弾の個数をχ+1から変化させて都合の良い数字にする必要があるということです。つまり、
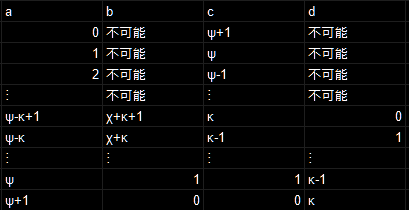
こういうことです。こちらのほうが正しい内訳になります。
何故先程の内訳が間違っていたか摘示します。要は、χ+1が必ずκより大きいという保証がないためです。もしκがχ+1よりも大きい場合、bの爆弾の個数がマイナスへ突入してしまいます。
なので必ず右上の爆弾の個数はκの文字を含んでいる必要性があるのです。つまり正しいルールは、

おそらくこうなるでしょう。少なくともこの部分(?の部分)に共通のマスを持つ情報指定の関係性は常にこの様になるはずです。同様に下記も成り立ちます。

さらにそこから、同じ文字に-1を代入できる場合はその字数を下げることができます。結局下記になります。


以上がチュートリアルの答えの検討になります。このくらいは証明というか、実際に真偽値表のようなものを表して考える必要があります。(直感で解ける人はいるんでしょうか。いたら私に教えて下さい。)
2025年1月21日追記
@伊藤さんより下記の通りコメントを頂きました。
さらに改良できました。横に線を作る方についてで、
左上が、Y+π、右上がX+K、右下がY+Kのとき、X+πの線が引けます。これは、4つのラインが一周する場合の対称性を考慮して見つけました。

コメントでご指摘いただいた内容のルールについては、上記のようになります。こっちのほうがスマートですね!
ちなみに言い訳をしておくと、このルールでチュートリアルは解けますが、正しいルールとして示したルールとは若干解ける範囲が違うはずです。(それぞれの文字に代入しても正しいルールとして示したルールを作れない為)
しかしチュートリアルの解説として、汎用化という面で見てこちらのほうがきれいで良いと思います。SUGOI。
ちなみにルールの内容について見てみると、ψ+πの範囲とχ+κの範囲が全く被っていない状態で、一部のマスの爆弾合計、つまり下段の爆弾合計がわかったとき、上段の爆弾の個数は自動的にそれらを引いた数になるというものです。記事中で使用した例を見てみると、

1と2の爆弾範囲があるうち、一部の範囲にはⅠ爆弾が入っていることが明らかである。さて、残りのマスにある爆弾の個数は?
1+2-1=2というわけですな。ルールを示されてから見てみれば簡単なのですが、盤面から検討するのはやはり難しい……。
ちなみに以上以下まで拡張できて、

こんな感じになりますが、これでどの範囲が解けるようになるかは未確認です。
改めまして、伊藤さんありがとうございました!
