
論理学とは何か:鹿島亮『数理論理学』を読んでいる①
著者 is 誰
一介のプログラマーで専門家ではない。数理論理学を趣味で勉強している。理工系大学院卒で数学などの最低限はやった模様。
以下5章までざっくりまとめ
1章
具体的な証明の例と証明図の導入
2章
構文論(シンタックス)に関する章である。構文論とは、人間や機械が記号操作的にやる世界のことである。
シンタックス(構文論)
セマンティクス(意味論)
この2つの違いが重要。
プログラムで言えば、ソースコードの記述ルール(文法)がシンタックス、その記述ルールを元にコンピューターが解釈して実際に動作を行う原理がセマンティクスだと言えよう。
論理学においても同様で、シンタックスとしての証明図(以下、図1)があるが、これは完全に記号操作のみの世界である。
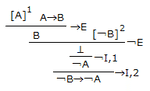
これを書くにあたって定義される公理とでも言うべきものはゲンツェンの考案した自然演繹の推論規則群である。(以下、図2)

ぱっと見意味不明なので詳細は本書や類書を読んで理解していただきたいが、ここに書いてある推論規則(ルール)「だけ」を使ってやるのが「証明図」(「導出図」とも言う)の作成である。
やってみればわかるが、命題(「私は人間である」など)の意味はここでは考えない。ここでやるのは記号と推論規則の操作だけである。
そして、この推論規則により導出される命題はすべて正しい!!
3、4章 健全性定理
そう、ゲンツェンの考案した(発見した?)自然演繹の推論規則に基づいて導出された命題はすべて意味論(セマンティクス)的にも正しいのである。
なぜそれが言えるかというと、本書の4章で証明される健全性定理というのが成り立つからである。
なので、つまり、自然演繹を使って機械的に証明するだけで良いんです。それをコンピューターにやらせて「自動証明」させるなんていう分野もある。
5章 完全性定理
さて、「自然演繹で導出した命題はすべて正しい」ことはわかったとして
じゃあ次の疑問が生じる
自然演繹ですべての正しい命題は証明できるの?
である。
これが保証されてないと困るのは、自然演繹でいくらこねくり回しても証明できない定理(命題)があると数学的に非常に困るからである。
すべての正しい定理は自然演繹で証明できないと困る。
つまり
自然演繹で証明できる => 正しい命題 (健全性:soundness)
正しい命題 => 自然演繹で証明できる(完全性:completeness)
この両方の矢印が成り立ってこそ我々の論理体系(今は述語論理の自然演繹体系)は安心して使えるのである。
そして、、、、、、、、
それはゲーデルによって証明された!!
天才的だね。
これにより安心を得たかに思われたが、では数学的命題はすべて完全性を持っているのだろうかという疑問が生まれる。
これについては自然数論の不完全性定理で否定されてしまうらしい。
6章以降
次は本丸の「不完全性定理」です!
実はまだ読み終わってない(理解してない)ので気が向いたらまた!!
アデュー!!!
続きはこちら
この記事が気に入ったらサポートをしてみませんか?
