
高校数学とシュレディンガー方程式
シュレディンガー方程式 という言葉を聞いたことがあるでしょうか?
「量子力学」や「シュレディンガーの猫」といった言葉を扱っているマンガやアニメが散見され、これらに関連して シュレディンガー方程式 という言葉を聞いたことがある人もいるかもしれません。
電子、原子、分子といったミクロサイズ対象物の運動を説明する式として、シュレディンガー方程式は扱われています。
私達の体を構成している最小単位(?)や、スマホ・PC・自動車・住宅といった、ありとあらゆるものがこういったミクロサイズ対象物から構成されているので、シュレディンガー方程式はミクロを扱う分野では、基本となる方程式の1つです。
(なお、サイズが大きくなると、計算量が膨大化するため、シュレディンガー方程式で解くにはとてもとても大変になるので、その場合は別の式(古典力学の式)を用います)
さて、シュレディンガー方程式は次のように書けます。
なお、話を単純化したいので、1次元の場合で考え、電子を扱うとします。
$$
i \hbar \frac{\partial }{\partial t} \Psi(x, t)
=
\{ - \frac{\hbar^{2}}{2 m} \frac{\partial^{2}}{\partial x^{2}} + V (x, t) \} \Psi (x, t)
$$
$${\Psi(x, t)}$$は、時刻$${t}$$における位置$${x}$$の電子の波動関数を表します。
さて、この式は、虚数$${i}$$を含んでいます。
私は初めてこの式を見たとき、とても驚きました。
$${i}$$が入っているからです。
$${i}$$は想像上の数であり、実在しないと高校数学の教科書で私は知りました。
なので、現実を記述するシュレディンガー方程式が$${i}$$を含んでいることがとても気持ち悪いと思いました。
このようなことから、例えば、ニュートン方程式やマクスウェル方程式と比べると、シュレディンガー方程式は数学的な難しさや物理的イメージが付きにくいと感じる人が多いと思います。
一方で、シュレディンガー方程式のざっくりとした導出過程は、実はそれほどハードルは高くなく、高校数学までの知識で導くことができます。
本記事の目的は、難しそうでとっつきにくいと感じるシュレディンガー方程式の導出手順を、高校数学までの知識を用いて紹介することで、シュレディンガー方程式に対するハードルを少しでも下げることです。
なお、本記事で使用する高校数学までの知識は以下です。
微分
三角関数
指数関数
複素数
行列
ベクトル
二次方程式(中学で習う)
ちなみに、私はど素人なので、物理的および数学的な厳密性は記述できないです。
なので、細かいミスや間違いはあると思いますが、ご容赦下さい。
致命的な誤りはたぶん無いと思います。
あったら、ごめんなさい。
以下が本記事の流れをざっと示す目次です。
シュレディンガー方程式を導く方針
さて、どういった手順でシュレディンガー方程式を求めるか考えたいです。シュレディンガー方程式は、電子といったとてもとても小さい対象を扱っているので、電子がどういった動きをしているか私達の目では見えないです。なので、従来からある古典物理の式をまずは参考にしてみましょう。
なんでそのように考えるのかは、次の通りです。
シュレディンガー方程式はミクロを扱う式ですが、ミクロをマクロ領域に持っていたときに、シュレディンガー方程式は古典物理の式と同じ形に変化すると考えるのが自然だろう、と思うからです。
古典力学から量子力学への置き換え試み
さて、物理は現実世界を扱っており、注目している対象のエネルギー、位置、運動量等を予測する分野です。
特に、エネルギーは重要な物理量の1つなので、古典力学におけるエネルギーの式を考えてみましょう。
また、話を簡単にしたいので、ポテンシャルが無い自由粒子のケースを考えましょう。
古典力学におけるエネルギーの式は次の通りです。
$$
E = \frac{P^{2}}{2 m}
$$
で、ここから量子化への移行を試みましょう。
量子力学の興味深い特徴は、粒子性と波動性の二重性です。先の古典力学の式$${E = \frac{p^{2}}{2 m} + V}$$では、エネルギー$${E}$$と運動量$${p}$$という物理量が含まれています。それらを量子力学的に表現したものは、以下の2つの式です。
$$
E = \hbar \omega \leftarrow エネルギーを波で表現
\\ \\
p = \hbar k \leftarrow 運動量を波で表現
$$
これら2式を$${E = \frac{P^{2}}{2 m}}$$に代入します。
$$
\hbar \omega
=
\frac{( \hbar k )^{2}}{2 m}
=
\frac{ \hbar^{2} k^{2} }{2 m}
$$
この式は、角周波数$${\omega}$$と波数$${k}$$が入っているので、この式の電子波の状態は以下進行波で表現できると仮定しましょう。
なお、後退波でも良いのですが、話を簡単にしたいので、ここでは進行波とします。
$$
\underline{進行波}
\\ \\
\Psi = A \sin (k x -\omega t)
$$
ここで、進行波と言いましたが、$${\Psi = A \sin (k x -\omega t)}$$を見て、進行波のイメージが付きにくい方がいらっしゃるかもしれませんので、補足説明させていただきます。話を簡単にしたいので、波の1点に注目します。
具体的には、例えば、位相$${\theta}$$がゼロのところを注目しましょう。
$$
\theta = k x -\omega t = 0
\\
\downarrow
\\
x = \frac{\omega}{k} t
$$
これは、中学数学の教科書に載っている$${y = a x + b}$$の形になっており、グラフ化すると以下のようになり、時間$${t}$$が経過していくと、波がxのプラス方向(進行方向)に進んでいくことが分かります。
なので、$${k x - \omega t}$$表示の場合、進行波と呼びます。

ちなみに、進行波のプラスをマイナスに換えた$${k x + \omega t}$$表示は、後退波と呼びます。
で、
$$
\hbar \omega
=
\frac{ \hbar^{2} k^{2} }{2 m} + V
$$
の左辺を見ると、$${\omega}$$が1個あります。これは$${\Psi = A \sin (k x -\omega t)}$$を1回微分すると良さげです。
$$
\frac{\partial}{\partial t} \Psi
=
\frac{\partial}{\partial t} A \sin(kx-\omega t)
=
A \cos(kx-\omega t) \times (- \omega)
=
- \omega A \cos(kx-\omega t)
$$
この式に$${- \hbar}$$を掛けると、$${\hbar \omega=\frac{ \hbar^{2} k^{2} }{2 m} + V}$$の左辺の形に近づきます。
$$
- \hbar \frac{\partial}{\partial t} \Psi
=
(\hbar \omega) A \cos(kx-\omega t)
$$
次に、
$$
\hbar \omega
=
\frac{ \hbar^{2} k^{2} }{2 m}
$$
の右辺を見ると、$${k}$$が2個あります。これは$${\Psi = A \sin (k x -\omega t)}$$を2回微分すると良さげです。
$$
\frac{\partial^{2}}{\partial x^{2}} \Psi
=
\frac{\partial^{2}}{\partial x^{2}} A \sin(kx-\omega t)
=
- k^{2} A \sin(kx-\omega t)
=
- k^{2} \Psi
$$
この式に$${- \frac{\hbar^{2}}{2 m}}$$を掛けると、$${\hbar \omega=\frac{ \hbar^{2} k^{2} }{2 m} + V}$$の左辺の形に近づきます。
$$
- \frac{\hbar^{2}}{2 m} \frac{\partial^{2}}{\partial x^{2}} \Psi
=
\frac{(\hbar k)^{2}}{2 m} \Psi
=
\frac{(\hbar k)^{2}}{2 m} A \sin(kx-\omega t)
$$
左辺と右辺を整理すると次の通りです。
$$
- \hbar \frac{\partial}{\partial t} \Psi
=
(\hbar \omega) A \underline{\cos(kx-\omega t)}
, \quad
- \frac{\hbar^{2}}{2 m} \frac{\partial^{2}}{\partial x^{2}} \Psi
=
\frac{(\hbar k)^{2}}{2 m} A \underline{\sin(kx-\omega t)}
$$
左辺=$${\hbar \omega}$$と右辺=$${\frac{(\hbar k)^{2}}{2 m}}$$の形に近づきましたが、波動関数が左辺側:$${A \cos(kx-\omega t)}$$、右辺側:$${A \sin(kx-\omega t)}$$となり、両辺が一致しないです。
一致しない理由は、微分の回数が1回と2回の違いがあるからです。
以上のことから、微分の回数が1回と2回でも$${\Psi}$$の形が変化しない波動関数を採用すると良さげです。
微分を行ってもその関数の形が変わらないものは高校数学の教科書に載っています。
それは、指数関数です。
例えば、$${y=a^{x}}$$です。
ただ、この形ですと周期性を示す波を表現できません。
そこで、指数関数、ネイピア数、三角関数、虚数といった数学で重要な要素を組み合わせたオイラーの公式と呼ばれるものを使いましょう。
オイラーの公式は次の通りです。
$$
e^{\pm i \theta} = \cos \theta \pm i \sin \theta
$$
オイラーの公式をいじくると、$${\sin \theta}$$と$${\cos \theta}$$の形に持っていくことができます。
なので、三角関数をオイラーの公式に置き換えても良さそうです。
$$
e^{i \theta} = \cos \theta + i \sin \theta,
\quad
e^{- i \theta} = \cos \theta - i \sin \theta
\\ \\
\downarrow
\\ \\
\sin \theta = \frac{e^{i \theta} - e^{- i \theta}}{2 i},
\quad
\cos \theta = \frac{e^{i \theta} + e^{- i \theta}}{2}
$$
ということで、波動関数を$${\Psi = A \sin(kx-\omega t)}$$から$${\Psi = A e^{i (kx-\omega t)}}$$に置き換えてみましょう。
上述と同様な計算をすると、自由粒子のシュレディンガー方程式を得ます。
$$
左辺側
=i \hbar \frac{\partial}{\partial t} \Psi
= (\hbar \omega) A e^{i (kx-\omega t)}
=(\hbar \omega) \Psi, \\ \\
\quad
右辺側
=\frac{\hbar^{2}}{2 m} \frac{\partial^{2}}{\partial x^{2}} \Psi
=\frac{(\hbar k)^{2}}{2 m} A e^{i (kx-\omega t)}
=\frac{(\hbar k)^{2}}{2 m} \Psi
\\ \\
\downarrow
\\ \\
\underline{自由電子のシュレディンガー方程式}
\\ \\
i \hbar \frac{\partial}{\partial t} \Psi
=
\frac{\hbar^{2}}{2 m} \frac{\partial^{2}}{\partial x^{2}} \Psi
$$
この式は、電子が外力を受けていない状態です。例えると、宇宙飛行士が宇宙ステーションでプカプカ自由に浮いているような状態をテレビ等で見たことがあると思いますが、そんな状態が自由電子だと思っていただければと思います。
というわけで、自由電子といった特殊なケースではありますが、古典力学の式から量子化を試みることで基本的なシュレディンガー方程式を得ました。
これで、まずはスタートラインに着きました。
一般なケースにおけるシュレディンガー方程式
しかし、私達が暮らしている日常では、電子は電場や磁場といった力場の中にいる場合が、一般的だと思います。
こういった力場はポテンシャルエネルギー$${V}$$と呼ばれます。
なので、ポテンシャルエネルギー$${V}$$中にいる電子のシュレディンガー方程式がどういう形になるのかを考えてみましょう。
考え方としては、再度古典力学を参考にしましょう。
運動エネルギー$${\frac{p^{2}}{2 m}}$$とポテンシャルエネルギー$${V}$$を足したものが全エネルギー$${E}$$になります。
$$
E = \frac{p^{2}}{2 m} +V
$$
自由電子のシュレディンガー方程式は、上述の通り、以下のように導きました。
$$
E = \frac{P^{2}}{2 m}
\rightarrow
\hbar \omega
=
\frac{ \hbar^{2} k^{2} }{2 m}
\rightarrow
i \hbar \frac{\partial}{\partial t} \Psi
=
\frac{\hbar^{2}}{2 m} \frac{\partial^{2}}{\partial x^{2}} \Psi
$$
なので、この式を参考にして、ポテンシャルエネルギー$${V}$$中にいる電子のシュレディンガー方程式は次のように書いてみてはどうでしょうか?
$$
\underline{ポテンシャルエネルギーV中にいる電子のシュレディンガー方程式}
\\ \\
E = \frac{p^{2}}{2 m} +V
\rightarrow
\hbar \omega
=
\frac{ \hbar^{2} k^{2} }{2 m} + V
\rightarrow
i \hbar \frac{\partial}{\partial t} \Psi
=
\{ \frac{\hbar^{2}}{2 m} \frac{\partial^{2}}{\partial x^{2}} + V \} \Psi
$$
ここで、$${\frac{\hbar^{2}}{2 m} \frac{\partial^{2}}{\partial x^{2}} + V}$$はエネルギーを表す部分です。
また、長ったらしいので、省略して$${\hat{H} = \frac{\hbar^{2}}{2 m} \frac{\partial^{2}}{\partial x^{2}} + V}$$と書いてみましょう。
なお、$${\hat{H}}$$はハミルトニアンという名前が付いています。
あと、ポテンシャルエネルギー$${V}$$中にいる電子のシュレディンガー方程式は、一般のシュレディンガー方程式とも呼ばれているそうです。
さて、一般のシュレディンガー方程式は、虚数$${i}$$が入っています。
また、先に紹介した波動関数$${\Psi}$$は次のように複素数の形を取っています。
$$
\Psi
=
A e^{i (kx-\omega t)}
=
A \{ \cos (kx-\omega t) + i \sin (kx-\omega t) \}
\\ \\
=
A \cos \theta + i A \sin \theta
=
a + i b
$$

このように、一般のシュレディンガー方程式は複素数を含んでおり、電子といったミクロ対象の運動を記述します。
私達が暮らす世界は(表面上?)実数ですが、私達の根本を構成するミクロなものが複素数に従うと仮定するのは、とてもとても不思議です。
もはや、私達の通常の直感が及びにくい領域です。
定常状態におけるシュレディンガー方程式
さて、これで一般のシュレディンガー方程式を導きました。
$$
\underline{一般のシュレディンガー方程式}
\\ \\
i \hbar \frac{\partial}{\partial t} \Psi (x, t)
=
\{ \frac{\hbar^{2}}{2 m} \frac{\partial^{2}}{\partial x^{2}} + V (x, t) \} \Psi (x, t)
$$
しかし、不器用で要領が悪い私は、この式を見ても電子の振る舞いをイメージできないです。
なので、もう一歩踏み込んでより具体的なケースを考えてみたいです。
自由電子は真っすぐしか飛んでいないので、もの足りないですし、実用的では無いです。
そこで、より具体的かつシンプルな系、例えば、水素原子を考えてみたいです。
水素原子は、電子1個と陽子1個で構成されているそうです。
陽子は太陽みたいなもので、電子は地球のように太陽の周りをグルグル回っていると仮定しましょう。
話しを簡単にしたいので、陽子を中心に電子はとある平面のみを円運動をするとしましょう。
このとき、電子の波はどのように動くでしょうか?
先ほど、進行波と後退波の話をしました。
波の動きとしては、この2通りあると仮定しましょう。
さて、電子は進行波と後退波どちらの動きをするでしょうか?
あるときは進行波でしょう。
また、あるときは後退波でしょう。
おそらく、電子は進行波が好き、後退波が好き、といったえり好みはしないと思います。
なので、等しい確率で進行波と後退波を選ぶのではないかと思います。
これは、陽子を中心に電子が時計回りの円軌道と反時計回りの円軌道を等しく行うことになります。
で、この現象は古典力学の観点で言うと、進行波と後退波をぶつけあって干渉させた結果、波の振幅が時間の経過とともに上下運動をして、波自体があたかも動いていないように見える定在波と呼ばれる現象に対応します。
量子力学では、この定在波を取る条件が、ボーアの量子条件と呼ばれているみたいです。
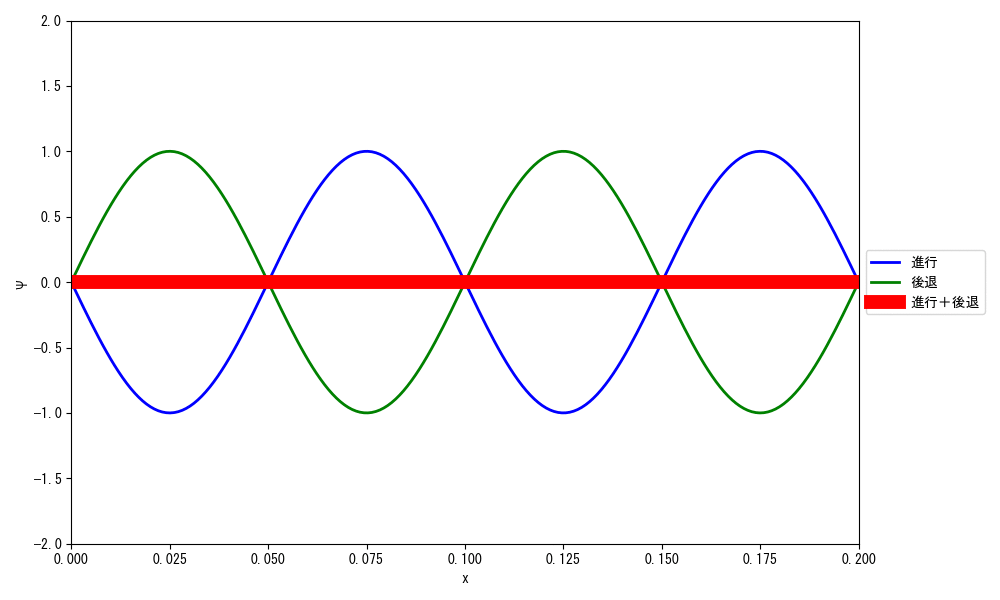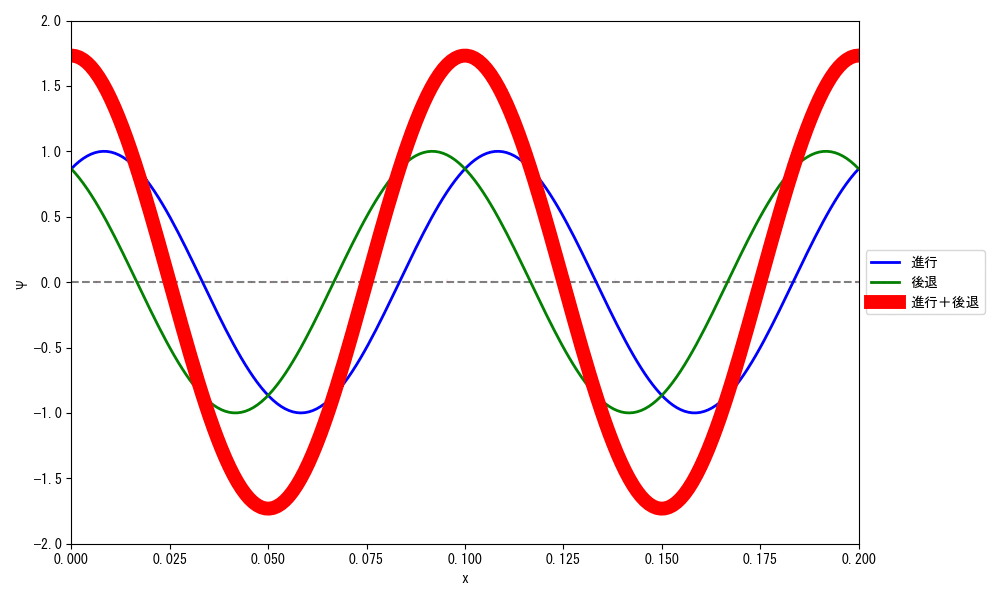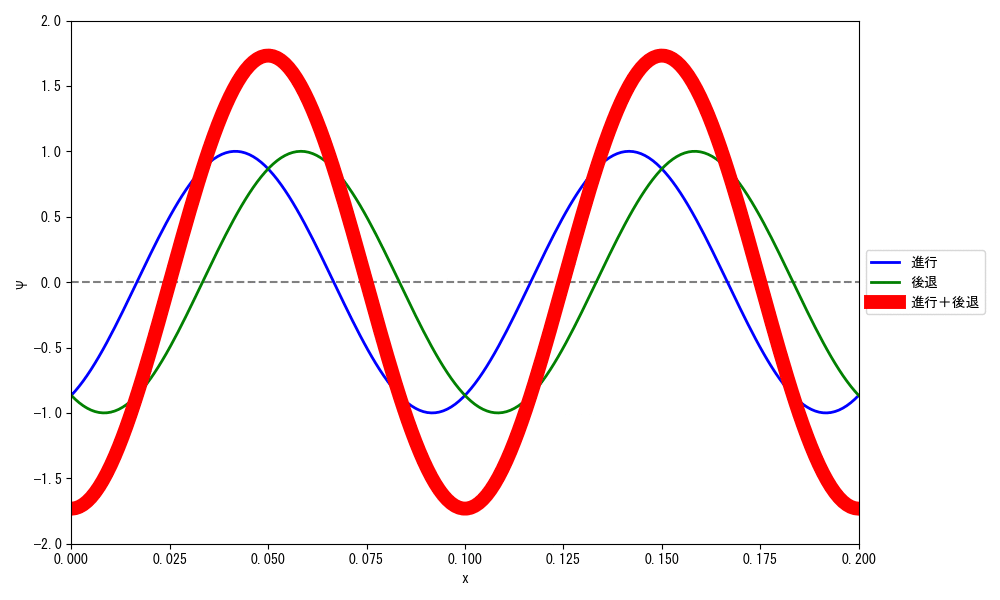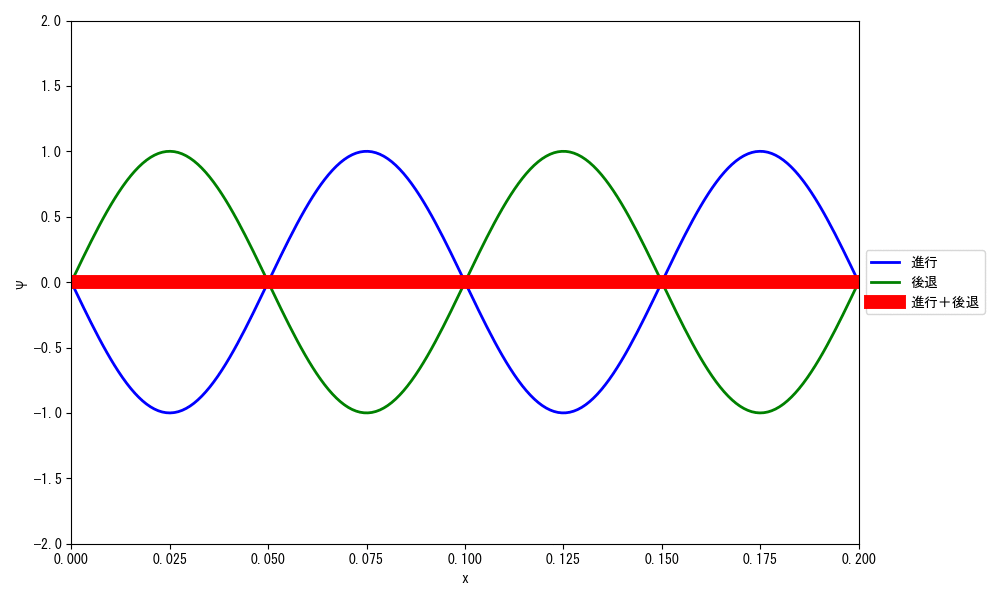
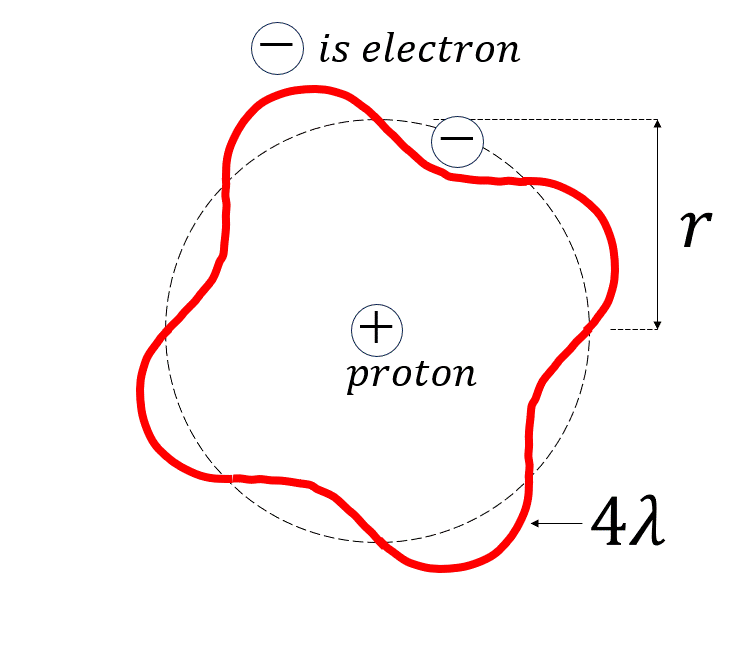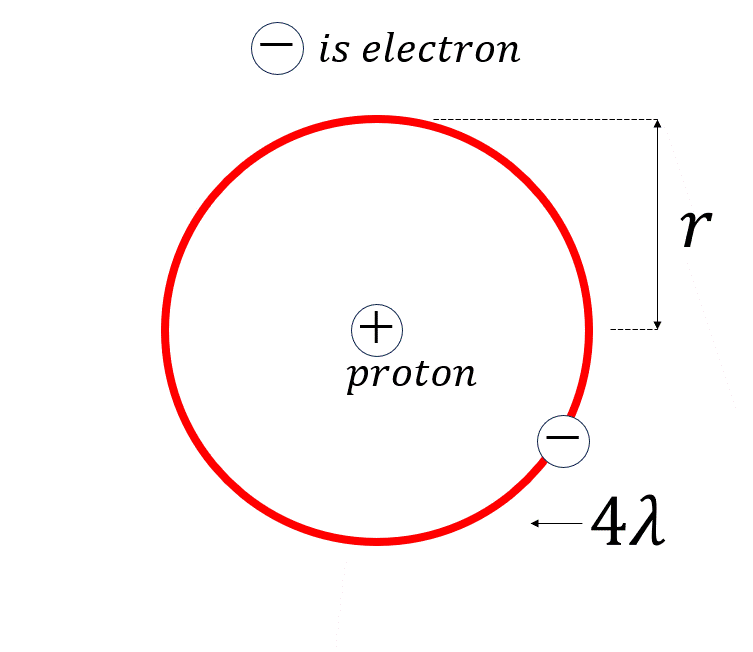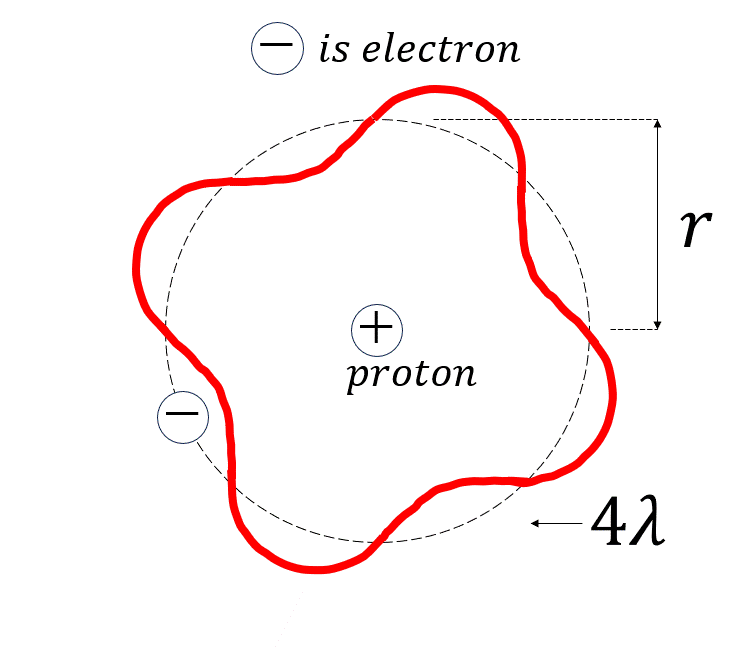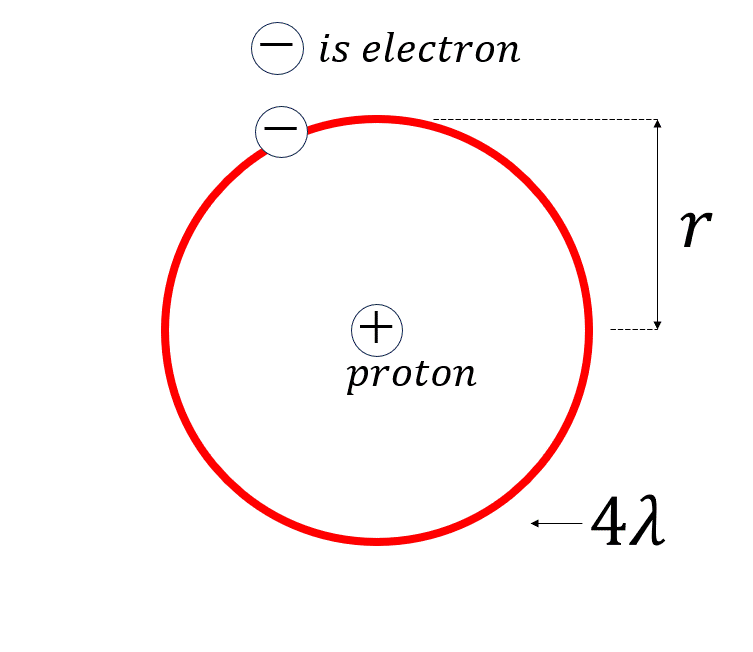
さて、定在波を式の形で表現してみましょう。
視覚的に分かりやすいサイン波で考えてみましょう。
進行波と後退波は次の通りです。
$$
\Psi_{進行} = A \sin (k x - \omega t), \quad \Psi_{後退} = A \sin (k x + \omega t)
$$
定在波は、進行波と後退波がぶつかったものなので、次の形になります。
$$
\Psi_{定在} = \Psi_{進行} + \Psi_{後退}
\\ \\
=A \sin (k x - \omega t) + A \sin (k x + \omega t)
\\ \\
\downarrow \quad 加法定理
\\ \\
A \underbrace{\sin kx}_{位置x} \underbrace{\cos \omega t}_{時間t}
$$
さて、この定在波の式は興味深い形をしています。
何が興味深いかと言いますと、関数$${x}$$と関数$${t}$$の掛け算の形をしていることです。
つまり、波動関数$${\Psi}$$は次の形で書けることです。
$$
\Psi(x, t) = \psi(x) \phi(t)
$$
また、ポテンシャルエネルギー$${V(x, t)}$$についても考えてみましょう。
電子と陽子は、地球と太陽の関係に対応しています。地球と太陽の間に万有引力が働くように、電子と陽子の間には電気の力:クーロン力が働きます。
この力は、電子と陽子が近づくほど大きくなります。
これを式で表すと以下の通りです。
$$
V(x) = \frac{(-e_{電子}) \times (+e_{陽子})}{x} = - \frac{e^{2}}{x}
$$

この式は、時間$${t}$$が含まれていないです。
つまり、電子が感じるポテンシャルエネルギーは、電子と陽子の間の距離$${x}$$のみが決定権があり、時間$${t}$$はどの時間でもいいよ、ということを言っています。
なので、上述した水素原子モデルにおける一般のシュレディンガー方程式は次のように形を変えることができそうです。
$$
\underline{一般のシュレディンガー方程式}
\\ \\
i \hbar \frac{\partial}{\partial t} \Psi (x, t)
=
\{ \frac{\hbar^{2}}{2 m} \frac{\partial^{2}}{\partial x^{2}} + V (x, t) \} \Psi (x, t)
\\ \\
\downarrow
\\ \\
\underline{定在波状態の水素原子のシュレディンガー方程式}
\\ \\
i \hbar \frac{\partial}{\partial t} \{ \psi(x) \phi(t) \}
=
\{ \frac{\hbar^{2}}{2 m} \frac{\partial^{2}}{\partial x^{2}} + V (x) \} \{ \psi(x) \phi(t) \}
\\ \\
\downarrow
\\ \\
\underline{tの偏微分は\psi(x)に影響しない、xの偏微分は\phi(t)に影響しないので}
\\ \\
\downarrow
\\ \\
\psi(x) \times i \hbar \frac{\partial}{\partial t} \phi(t)
=
\phi(t) \times \{ \frac{\hbar^{2}}{2 m} \frac{\partial^{2}}{\partial x^{2}} + V (x) \} \psi(x)
\\ \\
\downarrow
\\ \\
\underline{両辺を\psi(x) \phi(t)で割ると}
\\ \\
\downarrow
\\ \\
\underbrace{i \hbar \frac{1}{\phi(t)} \frac{\partial}{\partial t} \phi(t)}_{tのみ}
=
\underbrace{\frac{1}{\psi(x)} \{ \frac{\hbar^{2}}{2 m} \frac{\partial^{2}}{\partial x^{2}} + V (x) \} \psi(x)}_{xのみ}
$$
さて、$${i \hbar \frac{1}{\phi(t)} \frac{\partial}{\partial t} \phi(t)=\frac{1}{\psi(x)} \{ \frac{\hbar^{2}}{2 m} \frac{\partial^{2}}{\partial x^{2}} + V (x) \} \psi(x)}$$は、左辺が時間$${t}$$の関数、右辺が位置$${x}$$の関数であり、$${t}$$の関数と$${x}$$の関数がイコールと言っているので、こういった場合は両辺が何らかの定数としておかないと、この式を成り立ちません。
そこで、定数をとりあえず$${E}$$としましょう。
そうしますと、次の2式を得ます。
$$
\underline{時間に依存する部分}
\\ \\
i \hbar \frac{\partial}{\partial t} \phi(t)
=
E \phi(t)
\\ \\
\\ \\
\underline{位置に依存する部分}
\\ \\
\{ \frac{\hbar^{2}}{2 m} \frac{\partial^{2}}{\partial x^{2}} + V (x) \} \psi(x)
=
E \psi(x)
\quad \rightarrow \quad
\hat{H} \psi(x)
=
E \psi(x)
$$
さて、時間に依存する部分:$${i \hbar \frac{\partial}{\partial t} \phi(t) =E \phi(t)}$$は、$${\frac{\partial y}{\partial x} = y}$$の形をしています。
これは、1回微分して元の関数の形を取る、すなわち、変わらない特別な式です。
1回微分して、元の形を取る特殊な関数は高校数学の教科書に書かれています。
それは、指数関数$${y=e^{a x}}$$です。
$${\phi(t) = A e^{a t}}$$と仮定して、時間に依存する部分:$${i \hbar \frac{\partial}{\partial t} \phi(t) =E \phi(t)}$$に代入してみましょう。
$$
\underbar{時間に依存する部分}
\\ \\
i \hbar \frac{\partial}{\partial t} \phi(t) =E \phi(t)
\underbrace{\rightarrow}_{\phi(t) = A e^{a t}}
i \hbar \frac{\partial}{\partial t} A e^{a t} =E A e^{a t}
\\ \\
\rightarrow
i \hbar \sout{A} a \sout{e^{a t}} = E \sout{A e^{a t}}
\rightarrow
a = - i \frac{E}{\hbar}
\rightarrow
\phi(t) = A e^{- i \frac{E}{\hbar} t}
$$
$${\phi(t) = A e^{- i \frac{E}{\hbar} t}}$$は$${A}$$が決まっていないので気持ち悪いです。
なので、$${A}$$を出しましょう。
$${e^{- i \frac{E}{\hbar} t} = 1}$$の形にすることができれば、$${A}$$が出そうです。
つまり、初状態である$${t=0}$$を$${\phi(t) = A e^{- i \frac{E}{\hbar} t}}$$に代入すれば良さげです。
$$
\underbar{時間に依存する部分}
\\ \\
\phi(t) = A e^{- i \frac{E}{\hbar} t}
\underbrace{\rightarrow}_{t=0}
\phi(t=0) = A \times 1
\rightarrow
\phi(t) = \phi(t=0) e^{- i \frac{E}{\hbar} t}
$$
というわけで、時間に依存する部分:$${i \hbar \frac{\partial}{\partial t} \phi(t) =E \phi(t)}$$の波動関数$${\phi(t)}$$は以下の形をすることが分かりました。
$$
\underbar{時間に依存する部分}
\\ \\
i \hbar \frac{\partial}{\partial t} \phi(t) =E \phi(t)
\rightarrow
\phi(t) = \phi(t=0) e^{- i \frac{E}{\hbar} t}
$$
時間に依存する部分:$${i \hbar \frac{\partial}{\partial t} \phi(t) =E \phi(t)}$$の話が一段落したので、次に位置に依存する部分:$${\{ \frac{\hbar^{2}}{2 m} \frac{\partial^{2}}{\partial x^{2}} + V (x) \} \psi(x)=E \psi(x) \rightarrow \hat{H} \psi(x)=E \psi(x)}$$を考えていきたいと思います。
左辺のハミルトニアン$${\hat{H} = \frac{\hbar^{2}}{2 m} \frac{\partial^{2}}{\partial x^{2}} + V (x) }$$はエネルギーを表すので、先述の通り、適当に置いた定数$${E}$$はエネルギーの値を表します。これは、重要な物理量の1つです。エネルギーが分かることで、私達は技術開発設計の効率が上がるからです。
演算子
ここで、位置に依存する部分:$${\hat{H} \psi(x)=E \psi(x)}$$をもう少し眺めてみましょう。
この式は、$${\hat{H}}$$が$${\psi(x)}$$に作用し、計算結果が得られる、というように解釈できます。
こういった解釈をしましたので、作用する機能を持つものを演算子と名付けてみましょう。
以下に簡単な具体例を考えてみましょう。
$$
\underbrace{3}_{演算子} \times \underbrace{4}_{作用される対象} = \underbrace{12}_{計算結果}
$$
この例ですと、作用される 4 は 12 と変換され、作用前の状態:4と作用後の状態:12は異なります。
なので、演算という行為は、一般的には作用される対象の形は変化すると言えそうです。
ただ、中には変化しないケースもあると思います。
それが、上述の
$$
\underline{位置に依存する部分}
\\ \\
\hat{H} \psi(x)=E \psi(x)
$$
です。
これは、$${\hat{H}}$$が$${\psi(x)}$$に作用するのですが、出力結果として$${\psi(x)}$$はその関数形を保持しており、その代わり$${E}$$倍膨らむイメージです。
これは、物理的な解釈としては、電子の情報を含んでいる波動関数$${\psi(x)}$$に対してエネルギー演算子である$${\hat{H}}$$を作用したら、エネルギー$${\bold{E}}$$が求まることになります。
位置と運動量を同時に測定してみる
さて、演算子という話をしたので、もう少し深堀してみましょう。
ハミルトニアン$${\hat{H} = - \frac{\hbar^{2}}{2 m} \frac{\partial^{2}}{\partial x^{2}} + V (x) }$$はポテンシャル$${V}$$中にいる電子のエネルギーを表す演算子です。
話しを簡単にしたいので、ポテンシャル$${V}$$を無くした形、すなわち、自由電子の場合を考えたいと思います。
そうしますと、ハミルトニアンは$${\hat{H}=- \frac{\hbar^{2}}{2 m} \frac{\partial^{2}}{\partial x^{2}} }$$です。
これは上述した古典力学における運動エネルギー$${\frac{p^{2}}{2 m} }$$に対応します。
量子力学:$${- \frac{\hbar^{2}}{2 m} \frac{\partial^{2}}{\partial x^{2}} }$$と古典力学:$${\frac{p^{2}}{2 m} }$$を見比べて、量子力学の運動量演算子$${p}$$を出しましょう。
$$
量子力学:- \frac{\hbar^{2}}{2 m} \frac{\partial^{2}}{\partial x^{2}}
=\frac{\hat{p}^{2}}{2 m}, \quad
古典力学:\frac{p^{2}}{2 m}
\\ \\
\downarrow
\\ \\
\hat{p}^{2} = - \hbar^{2} \frac{\partial^{2}}{\partial x^{2}}
\rightarrow
\hat{p} = \frac{\hbar}{i}\frac{\partial}{\partial x}
$$
ここで、さきほど演算という行為は「一般的には作用される対象の形は変化すると言えそうだ」と述べました。
この考え方を一歩進めて重要な物理量である位置$${x}$$と運動量$${p}$$を同時に求める試みをしてみましょう。
具体的には、次の計算です。
左は運動量を求めてから、位置を求めると解釈できそうです。
右はその逆で、位置を求めてから、運動量を求めると解釈できそうです。
$$
\underbrace{\hat{x} \hat{p} \psi(x)}_{運動量を求めてから、位置を求める}
, \quad
\underbrace{\hat{p} \hat{x} \psi(x)}_{位置を求めてから、運動量を求める}
$$
位置$${x}$$と運動量$${p}$$を同時に求めることは、上式を同時に実行するに対応しそうです。
私達の日常では、位置$${x}$$と運動量$${p}$$を同時に求めることは簡単であると認識されるでしょう。
簡単な具体例を考えてみましょう。
重量が1トンで、時速60km/hで走っている車がいるとしましょう。
何らかの測定器を準備すれば、この車の位置$${x}$$と運動量$${p = m v}$$を同時に測定することは、難しいことでは無いです。
つまり、同時観測が可能です。
言い換えると、「運動量を求めてから、位置を求める」と「位置を求めてから、運動量を求める」は同じ結果と言えそうです。

さて、量子力学の場合はどうなるか考えてみましょう。
上述の$${\underbrace{\hat{x} \hat{p} \psi(x)}_{運動量を求めてから、位置を求める}と\underbrace{\hat{p} \hat{x} \psi(x)}_{位置を求めてから、運動量を求める} }$$を引き算してみましょう。
同時に観測が可能でしたら、引き算の結果はゼロになるはずです。
$$
\underbrace{\hat{x} \hat{p} \psi(x)}_{運動量を求めてから、位置を求める}
-
\underbrace{\hat{p} \hat{x} \psi(x)}_{位置を求めてから、運動量を求める}
\\ \\
=
\hat{x} \{ \frac{\hbar}{i}\frac{\partial}{\partial x} \psi(x) \}
-
\frac{\hbar}{i}\frac{\partial}{\partial x} \{ \hat{x} \psi(x) \}
\\ \\
=\frac{\hbar}{i} \{ x\frac{\partial}{\partial x} \psi(x) - \psi(x) - x \frac{\partial}{\partial x} \psi(x)\}
=
- \frac{\hbar}{i} \psi(x)
=
i \hbar \psi(x)
\\ \\
\downarrow 整理すると
\\ \\
\hat{x} \hat{p} - \hat{p} \hat{x} = i \hbar
$$
不思議なことに、引き算の結果がゼロでは無いです。
この結果のように、量子力学の場合、ミクロの世界では位置$${x}$$と運動量$${p}$$を同時に求めることは本質的にできないことをこの式は示唆していると解釈できそうです。
で、何で同時に観測できないかと言いますと、ミクロな対象物の粒子と波動の二重性が根本的な理由となります。
位置$${x}$$と運動量$${p}$$を同時に求めることは本質的にできない、という主張が正しいか否かは実験結果に基づきます。
量子力学の発見以降、これに矛盾した大ニュースは今のところ無いんですかね?
私は存じておりません。
定常状態&空間と時間分離した波動関数の形
さて、話を戻しましょう。
時間に依存する部分と位置に依存する部分の波動関数の形が分かったので、時間と位置が混ざった波動関数が求まります。
$$
\underbar{時間に依存する部分}
\\ \\
i \hbar \frac{\partial}{\partial t} \phi(t) =E \phi(t)
\rightarrow
\phi(t) = \phi(t=0) e^{- i \frac{E}{\hbar} t}
\\ \\
\\ \\
\underline{位置に依存する部分}
\\ \\
\hat{H} \psi(x)=E \psi(x)
\\ \\
\\ \\
\underline{時間と位置が混ざった波動関数}
\\ \\
\Psi (x, t) = \psi(x) \phi(t) \ = \psi(x) \phi(0) e^{- i \frac{E}{\hbar} t}
$$
さて、$${\hat{H} \psi(x)=E \psi(x)}$$は数学的には、$${\psi(x)}$$に対して適当な定数$${k}$$を掛け算(※)しても、式が成り立ちます。
※:$${\psi(x)}$$が$${k}$$倍膨らむ
具体的にお示しましょう。
$$
\hat{H} \psi(x)=E \psi(x)
\rightarrow
\hat{H} (k \psi(x))=E (k \psi(x))
\\ \\
\rightarrow
k \times \hat{H} \psi(x)=k \times E \psi(x)
\rightarrow
\hat{H} \psi(x)=E \psi(x)
$$
$${\phi(0)}$$を$${k}$$と見なすと、$${\psi(x)}$$と$${\psi(x)\phi(0)=\phi(0) \psi(x)= k \psi(x) = \psi(x)}$$と置き換えることができるので、時間と位置が混ざった波動関数は次のようにスッキリした形になります。
$$
\underline{時間と位置が混ざった波動関数}
\\ \\
\Psi (x, t) = \psi(x) \phi(t) \ = \psi(x) \phi(0) e^{- i \frac{E}{\hbar} t}=\psi(x)e^{- i \frac{E}{\hbar} t}
$$
さて、$${\psi(x)}$$でも$${k_{1} \psi(x)}$$でも$${k_{2} \psi(x)}$$でも$${k_{3} \psi(x)}$$でも解となるのは、不安定で気持ち悪いですね。
この気持ち悪さを解消するには、物理的にリーズナブルな束縛条件を加える(※)ことで、ただ1つの解を求めることができます。
※:境界条件や確率保存条件とか
行列とシュレディンガー方程式
あと、位置に依存する部分:$${\hat{H} \psi(x)=E \psi(x)}$$の形は、実は高校数学の教科書に載っています。
$${\hat{H} \psi(x)=E \psi(x)}$$のような式は固有値方程式、$${E}$$は固有値、$${\psi(x)}$$は固有ベクトル(固有関数)と呼ばれます。
これらは、高校数学教科書のベクトルや行列で出てきます。
$$
\underline{位置に依存する部分}
\\ \\
\underbrace{\hat{H} \underbrace{\psi(x)}_{固有ベクトル}=\underbrace{E}_{固有値} \underbrace{\psi(x)}_{固有ベクトル}}_{固有方程式}
$$
さて、これまで関数をメインで話しをしてきましたが、ここでベクトルや行列の話が出てきました。
なので、位置に依存する部分:$${\hat{H} \psi(x)=E \psi(x)}$$をベクトルや行列形式で考えてみましょう。
シンプルで実用的な例で考えてみましょう。
具体的には、2状態系です。
これは2の状態を考えています。デジタルの0、1やスイッチのON、OFF状態に対応すると思って下さい。
シンプルなケースですが、応用上とてもとても重要な概念です。
この場合、$${\psi(x)}$$を次のように表現してみましょう。
$$
\psi(x) = a_{1} \chi_{1} + a_{2} \chi_{2}
\rightarrow
\underbrace{a_{1}}_{1の確率振幅} \underbrace{\chi_{1}}_{状態1} + \underbrace{a_{2}}_{2の確率振幅} \underbrace{\chi_{2}}_{状態2}
$$
$${a_{1}}$$、$${a_{2}}$$は状態1と状態2の発生確率に関係する係数です。
$${\psi(x)}$$はこれまで関数の形で表現していましたが、これをベクトルの形で表現してみましょう。
$$
\psi(x)
\rightarrow
\ket\psi = \begin{bmatrix} a_{1} \\ a_{2} \end{bmatrix}
$$
これは2行1列の行列です。
$${\hat{H}}$$は$${\ket\psi}$$に作用する演算子なので、$${\hat{H}}$$は2行2列になると仮定しましょう。
$$
\underline{位置に依存する部分}
\\ \\
\hat{H} \psi(x)=E \psi(x)
\rightarrow
\hat{H} \ket \psi=E \ket \psi
\\ \\
\rightarrow
\begin{pmatrix} H_{11} & H_{12} \\ H_{21} & H_{22} \end{pmatrix}
\begin{bmatrix} a_{1} \\ a_{2} \end{bmatrix}
=
E
\begin{bmatrix} a_{1} \\ a_{2} \end{bmatrix}
\\ \\
=
E
\hat{1}
\begin{bmatrix} a_{1} \\ a_{2} \end{bmatrix}
=
E
\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}
\begin{bmatrix} a_{1} \\ a_{2} \end{bmatrix}
$$
この式を整理すると以下のようになります。
$$
\underline{位置に依存する部分}
\\ \\
\hat{H} \psi(x)=E \psi(x)
\rightarrow
\begin{pmatrix} H_{11} - E & H_{12} \\ H_{21} & H_{22} - E \end{pmatrix}
\begin{bmatrix} a_{1} \\ a_{2} \end{bmatrix}
=
\begin{bmatrix} 0 \\ 0 \end{bmatrix}
$$
さて、私達は2状態系の波動関数$${\begin{bmatrix} a_{1} \\ a_{2} \end{bmatrix}}$$を求めたいです。
$${\begin{bmatrix} a_{1} \\ a_{2} \end{bmatrix}}$$を求めるためには、$${\begin{pmatrix} H_{11} - E & H_{12} \\ H_{21} & H_{22} - E \end{pmatrix} }$$が逆行列を持たないこと、すなわち、以下を満たす必要があります。
$$
\begin{vmatrix} H_{11} - E & H_{12} \\ H_{21} & H_{22} - E \end{vmatrix}
=
0
$$
この式は高校数教科書の行列で出てきます。
この式を計算していきましょう。
$$
\begin{vmatrix} H_{11} - E & H_{12} \\ H_{21} & H_{22} - E \end{vmatrix}
=
E^{2} - (H_{11} + H_{22})E + (H_{11} H_{22} - H_{12} H_{21})
=
0
$$
面白いことに、この式は中学数学教科書の2次方程式と似た形です。
$$
a x^{2} + b x + c = 0
\rightarrow
x = \frac{-b \pm \sqrt{b^{2}-4ac}}{2a}
$$
2次方程式の解の公式を利用して$${E}$$を求めましょう。
$$
E^{2} - (H_{11} + H_{22})E + (H_{11} H_{22} - H_{12} H_{21})
=
0
\\ \\
\downarrow
\\ \\
E_{状態1} = \frac{1}{2} \{ (H_{11} + H_{22}) - \sqrt{(H_{11} + H_{22})^{2} - 4 (H_{11} H_{22} - H_{12} H_{21})} \}
\\ \\
E_{状態2} = \frac{1}{2} \{ (H_{11} + H_{22}) + \sqrt{(H_{11} + H_{22})^{2} - 4 (H_{11} H_{22} - H_{12} H_{21})} \}
$$
これで、状態1と状態2のエネルギーが分かりました。
波動関数$${\psi(x) = a_{1} \chi_{1} + a_{2} \chi_{2} \rightarrow \begin{bmatrix} a_{1} \\ a_{2} \end{bmatrix}}$$の確率振幅$${a_{1}}$$と$${a_{2}}$$を求めるには、状態1と状態2のみを取る系を考えているので、$${|a_{1}|^{2} + |a_{2}|^{2} = 1}$$を加えて計算すると出てきます。
なお、$${\psi(x)_{状態1}}$$と$${\psi(x)_{状態2}}$$を出そうとしましたが、うまく一意的に導けなかったので、あきらめました。
行列表示と位置・運動量の同時測定の関係
さて、先ほど位置演算子$${\hat{x}=x}$$と運動量演算子$${\hat{p}=\frac{\hbar}{i}\frac{\partial}{\partial x}}$$を紹介し、ミクロな世界では位置と運動量が同時に測定できなさそうなことを紹介しました。
$$
\hat{x} \hat{p} - \hat{p} \hat{x} = \underbrace{i \hbar \neq 0}_{ゼロでは無い}
$$
で、何でこんなことを言い出したかといいますと、面白いことに行列もこういった性質を持っているからです。
行列$${\hat{A} = \begin{pmatrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end{pmatrix} }$$と$${\hat{B} = \begin{pmatrix} B_{11} & B_{12} \\ B_{21} & B_{22} \end{pmatrix} }$$に対して、$${\hat{x} \hat{p} - \hat{p} \hat{x}}$$と同じ計算:$${\hat{A} \hat{B} - \hat{B} \hat{A}}$$をしてみましょう。
$$
\hat{A} \hat{B}
=
\begin{pmatrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end{pmatrix}
\begin{pmatrix} B_{11} & B_{12} \\ B_{21} & B_{22} \end{pmatrix}
\\ \\
=
\begin{pmatrix} A_{11}B_{11}+A_{12}B_{21} & A_{11}B_{12}+A_{12}B_{22} \\ A_{21}B_{11}+A_{22}B_{21} & A_{21}B_{12}+A_{22}B_{22} \end{pmatrix},
\\ \\
\hat{B} \hat{A}
=
\begin{pmatrix} B_{11} & B_{12} \\ B_{21} & B_{22} \end{pmatrix}
\begin{pmatrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end{pmatrix}
\\ \\
=
\begin{pmatrix} A_{11}B_{11}+\underline{A_{21}B_{12}} & \underline{A_{12}B_{11}+A_{22}B_{12}} \\ \underline{A_{11}B_{21}+A_{21}B_{22}} & \underline{A_{12}B_{21}}+A_{22}B_{22} \end{pmatrix}
\\ \\
\downarrow 下線部が異なるので
\\ \\
\hat{A} \hat{B} - \hat{B} \hat{A}
\neq
0
$$
なので、行列$${\hat{A}}$$と$${\hat{B}}$$は、一般的には$${\hat{A} \hat{B} - \hat{B} \hat{A} \neq 0}$$と言えそうです。
このように種族が異なる代数と行列が同じ性質を示すことは面白いです。
$$
\underline{代数}
\\ \\
\hat{x} \hat{p} - \hat{p} \hat{x} = i \hbar \neq 0
\leftarrow
\hat{x}=x, \quad \hat{p}=\frac{\hbar}{i}\frac{\partial}{\partial x}
\\ \\
\underline{行列}
\\ \\
\hat{A} \hat{B} - \hat{B} \hat{A}
\neq
0
\leftarrow
\hat{A} = \begin{pmatrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end{pmatrix}, \quad \hat{B} = \begin{pmatrix} B_{11} & B_{12} \\ B_{21} & B_{22} \end{pmatrix}
$$
なので、演算子は代数表現と行列表現ができ、どちらを採用するかは、その時々の計算都合に合ったものを選べば良いと思います。
まとめ
以上のことから、高校までの数学を用いてシュレディンガー方程式の導出を紹介させていただきました。
シュレディンガー方程式は、特にこの数10年において、人類の科学技術発展に大きく貢献した式の1つだと思います。
なぜなら、科学技術の進歩により、ミクロ領域における加工や処理が可能になったからです。
半導体メモリの細線パターンが、1桁nmになっていることが良い例だと思います。
このサイズですと、量子効果が思いっきり出てきます。
シュレディンガー方程式は、私達が直接観察できない・感じられないミクロ領域を扱い、その解釈も容易では無いです。
ですが、基本的なシュレディンガー方程式の俯瞰は、意外なことに高校までの数学で出来ちゃいます。
高校までの数学を受講した人は、ある程度いると思います。
数学が嫌いな人は多いでしょうが(※)、高校数学で学んだ複素数や行列といったキーワードを思い出せば、とっつきにくいシュレディンガー方程式に対するしきいが下がる人が、もしかしたらいるかもしれません。
そういった訳で、本記事がどなたかのプラス材料になれば嬉しいです。
※:私も好きではないです。

個人的な話
さて、以下は恐縮ですが、私の個人的な話です。
高校時代に、虚数や行列を数学の授業で教わったときに、私は全く理解できませんでした。
虚数は、実在しないものなので、学び意義が理解できませんでした。
また、行列はでかいカッコに数をいっぱい入れるもので、「これが何の役に立つの?学び意味あるの?」と感じました。
こういったことから、不器用で要領が悪い私は、高校数学の大部分は理解できませんでした。
そんなわけで、高校卒業後に高校数学を学び直す二度手間を経験しました。
高校数学を学び直す過程で、量子力学の教科書を読んだときに、虚数や複素数を扱っていることに驚愕しました。
量子力学は、ミクロの物理現象を記述する体系です。
物理現象とは、現実世界を扱います。
現実世界のミクロ対象物の運動は、複素数に従っていることを知り、このときに初めて、自分なりに複素数を学ぶ意義を見出しました。
また、行列は演算表現に適していることも知りました。
また、複素数が電気回路計算を楽にする道具、行列が手計算では対処できない規模の計算ツールとして活用されることも高校卒業後に知りましたが、量子力学で採用されていることの方が、私にとっては腑に落ちました。
高校時代に、高校数学の教員に複素数や行列の活用事例を問い合わせましたが、回答がありませんでした。
おそらく、その教員もご存じでなかったのかもしれません。
後出しじゃんけんの発想になりますが、高校生の私が複素数や行列の活用事例を知ったら、もう少し高校数学に興味を持っていたかもしれません。
私は自分でも自覚していますが、意義を自分なりに見出さないとモチベーションが湧かない面倒な性格です。
で、前置きが長くなりましたが、何が言いたいのかと言いますと、ごくごく少数派でしょうが、私のような高校生や高校卒業生がいると思い、このことが本記事を書くモチベーションに繋がりました。
参考文献
佐川ら、量子力学 (物理学スーパーラーニングシリーズ)、Springer
砂川、量子力学、岩波書店
吉田、オイラーの贈物 類の至宝eiπ=-1を学ぶ、海鳴社
