ゲーム画面から視野(fov、画角、視野角）を測る方法

2024年12月27日 12:59

これは下記動画で解説している内容を活字でも解説し直したものです。
挿入される画像等は動画のスクショだったりするので、説明に最適化されてないかもしれませんがご了承ください。

視野とは？

目やカメラなどで見える映像の範囲を、角度で表現したもの。
下記画像は、垂直視野60°、水平視野91.5°ぐらいで撮影された映像。

ここで描画された映像の形が長方形なのは、単にカメラやゲームやモニターの都合でしかない。
人間の目で見てる景色は別に長方形じゃないし、視野の理屈の説明としては長方形じゃなくてもいい。
例えば円形だと、視野として必要なパラメータは1つだけになり分かりやすい。下記画像のように、見える範囲を円錐で表したものを「視円錐」という。

なお、視界のど真ん中…カメラ（視点）の真っ正面にあり、カメラから画面に向かって真っすぐ線を伸ばしたときに画面とちょうど交わる点のことを、視心（VC : Visual Center）という。
絵画などにおいては視心の場所を描き手が自由に変えられるが、一般的な3Dゲームの映像においては画面のど真ん中に視心があることになる。

視野を測るのに必要な「90度視円錐」と「距離点」

視野90度の範囲を表した円錐を「90度視円錐」という。ゲーム画面から視野を測るために重要な存在。

円錐の性質上、頂点の角度が90度であれば円錐の【底面の半径】と【高さ】は同じ長さということになり、
視点（カメラのある場所）と視心、それから視界の端っこ（図で言えば【底面の半径】の右端）の3点を線で結べば、直角二等辺三角形ができる。

これが非常に重要。
実際のゲーム画面をただ見ただけでは、その画面を撮影しているカメラの位置（視点）が分からない。カメラの位置が分からなければ視野の角度も測りようがない。
しかし、もし上記図における「視界の端と45度の線との交点」の位置が、ゲーム画面の情報だけから何らかの方法で分かれば…

→90度視円錐の【底面の半径】が分かる、視円錐の底面の円が描ける
→【底面の半径】と【高さ】は同じ長さなので、視心から視点までの長さが分かる
→視点の位置が分かる

→視点から画面端に向けて線を引けば視野が分かる

視点から画面の上下左右の端に線を引く。2本の線の間にできた角（∠）が求めたい視野。ここまで描けたら後は角度を分度器で測るなり、なんか計算で出すなり、画像・動画編集ツールの機能で炙りだすなりするだけ。

と、芋づる式に答えに辿り着ける。
で、さっき言った「視界の端と45度の線との交点」のことを「距離点(DP : Distance Point)」という。

つまり距離点を求めれば視野が分かる。

作図上で重要な補足

ここでは画面に向かって右方向に45度の線を引いて、画面の右端付近に距離点を見出したが、
これはたまたま俺が説明のために右を選んだだけで、実際には45度であればどんな方向に引いてもいい。
距離点は左にも上にも下にも、どこにでも見出せる。ただその際、必ず90度視円錐の底面の円周上にできる。

それから、視野を測るためにこんな3D描画をするのは大変なので、実際の作図作業は平面上でやる。
どうやるかというと、視野を表す線を、画面に向かってぐるっと回転させるようなイメージ。

平面図になった。視点は真下と真右にそれぞれ移動している、と解釈する。水色の線分がどれも同じ長さで赤い円の半径なので、視点も距離点も必ず同心円上に乗るし、真右の視点は距離点と全く同じ位置になっている。

距離点を把握するために一点透視図法を利用する

距離点を求めれば視野が分かる、ではどうやって距離点を求めるか。
ここで一点透視図法というものを用いる。

説明の順番が前後するが、まず一点透視図とは、立体空間を構成する縦・横・奥行きの3軸のうち、2軸が画面と平行になっている図のこと。

要するに、四角い箱をカメラに映したときに正面が完全にきれいな正方形や長方形になってる状態のこと。

こういう図を描く方法や理論を一点透視図法と呼ぶ。
が、ここでは絵を描くためにこの理論を使うんじゃなくて、
ゲーム画面をこの理論で描かれた図のような状態に持っていく、というトリッキーなことをする。

スプラトゥーン3のゲーム画面を一点透視図にしたもの。単純に目視で四角い箱の縦と横の線が寸分狂わずまっすぐになるまで、右スティック操作でカメラをひたすら微調整した。結構疲れます。

一点透視図の特徴として、画面に対して垂直に伸びる奥行きの線を、そのまま無限に奥へ伸ばし続けると、最終的に必ず視心と同じ位置に収束し、線が消失する。
この、線が消失する位置を消失点(VP : Vanishing Point)という。

普通のゲーム画面の場合、視心は画面の真ん中に来るので、一点透視図の消失点も画面の真ん中に来る。

一点透視図は消失点が1点なのでその名前がついている。
この記事では扱わないが、カメラの角度を少し変えると二点透視図や三点透視図にもなる。

3軸のうち１軸だけが画面と平行になる場合、二点透視図になる。この場合は縦だけ画面と平行で、横と奥行きに傾斜がついている。奥行きの消失点と横の消失点、2つの消失点ができる。

二点透視図でも視野の測定ができないわけではないが手順がややこしくなるので、ここでは一点透視図にしてほしい。

なお、ゲーム画面を一点透視図の構図にできた後に、カメラ（視点）がスライド移動するのは構わない。
なので一点透視図にした後にプレイヤーが動いたりしてカメラの位置が変わっても、カメラの向き（角度）が変わらなければ大丈夫。

この通り、カメラの位置だけ変えた場合、奥行きの線は変わらず画面真ん中の消失点に伸びる。

では、今度は画面に対して45度の角度をつけて奥に伸びていく線を引いてみる。
すると今までとは違う位置に向かって収束し、消失する。仮にこの消失する位置を45度消失点と呼ぶことにする。

地面のグリッド線は正方形を作っているので、その正方形の対角線が45度の線になる。それを無限に奥に伸ばしていくと、画面右端付近のある一点に消失した。

画面に対する角度の違いによって、それぞれ決まった位置に収束、消失する性質がある。

また、これらの消失点は全て水平一直線に並ぶ。この線を消失線という。
ゲーム画面を一点透視図にした場合、視心と消失点が必ず画面のど真ん中になるため、消失線も必ず画面の真ん中を水平に通ることになる。

消失点は必ず消失線上にあるため、ある角度の消失点を求めたい場合、その角度がついた1本の線と消失線との交点を求めるだけでよい。消失線が既知であれば、何本も奥に伸びる平行線を引く必要は無いってこと。

右に40度の角度がついた線1本と、消失線（画面の真ん中を水平に通る線）の交点を求めれば、それが40度消失点となる。1本でいいので楽。

ここまで説明してきた性質を踏まえると、視点から45度の角度をつけて奥に無限に伸ばした線も、45度消失点に向かって収束することになる。

画面真ん中の視心と、視点、それから45度消失点の3点を線分で結べば、
90度視円錐のときに説明したのと全く同じ直角二等辺三角形が出来上がる。

上記画像の緑の交点のことを距離点というんでしたね？

つまり、45度消失点＝距離点。

つまり、ゲーム空間における奥に向かって45度の線を引けばいい。
それと消失線（画面真ん中の水平な線）との交点が45度消失点となり、これがイコール距離点なので、後はそこから視円錐とかを作図していけば視野が測れる。

【補足】少し前にも言ったけど、左にも距離点はできる。左奥に45度の角度の線を引けば左側にも45度消失点ができるので。

ここまでのまとめ

ゲーム画面を一点透視図にする
奥に向かって45度の線を引き、45度消失点を求める（それが距離点となる）
視心を円の中心として距離点を通る円を描く（それが90度視円錐の底面となる）
視心から垂直および水平に伸ばした線と、円との交点を描く（それが視点になる）（より正確には、本来画面手前にある視点を画面と同じ平面まで回転移動させてきた位置）
そこから画面端に向かって線を引けば、垂直視野と水平視野が分かる

実例

Splatoon3の場合

手動でカメラ角度を調整し、画面を一点透視図にする。
このとき、後で説明するが床などに正方形の線やオブジェクトが存在する状態にすること。
構図が決まったらその画面をキャプチャし、画像編集ソフトなり動画編集ソフトなりで開く。

最初に、そのキャプチャ画面が本当に一点透視図になっているかどうかを試そう。
ゲーム空間における真っすぐ奥に伸びる線を、編集ソフトの直線ツールなどを使って何本かなぞり、全てが画面の真ん中で交わることを確認する。
これが真ん中にならない場合はカメラの角度調整に失敗している。最初からやり直し。

床のタイルの線、画面左の高台の辺、画面中央やや右のブロックの辺などを水色の線でなぞった結果、ちゃんと画面の真ん中に収束することが分かった。

上手く一点透視図になっていることが確認出来たら、消失線もついでに引いておく。
画面真ん中を通る縦線も後で必要なので引いておく（これはこれで消失線なのだが、本題から逸れるのでここでは説明しない）

次は距離点を求めるために、奥に向かって45度の線を引く。具体的には床などにある正方形の対角線を引けばよい。
ここで、ゲーム空間における45度を正確に把握するために正方形を画面に映しておく必要があった。

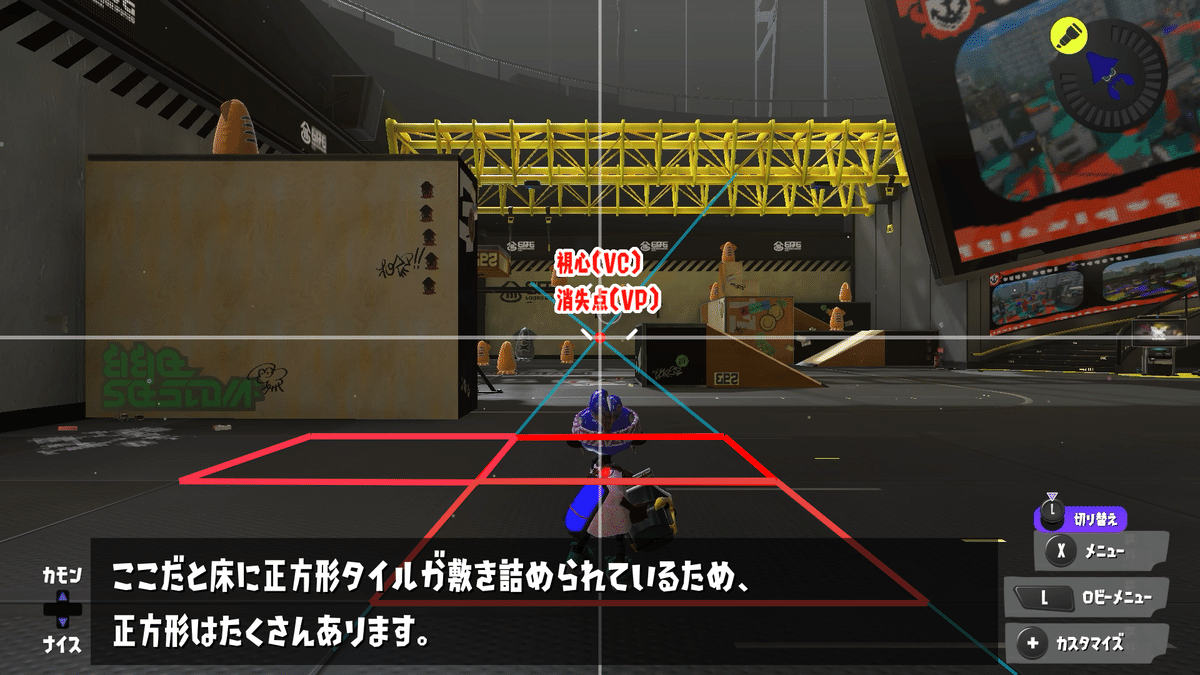
分かりにくいが床に正方形のパネルが敷き詰められているため、たくさんの正方形が画面にある状態。その対角線を引けば距離点が分かる。

もし、ゲーム空間における45度が精確に分かる方法が他にもあるなら、別に正方形を利用しなくてもいい（例えば地面と水平かつピッタリ45度の角度でビームを撃つ技があるとか？）

理論上は最低1本引けば距離点が分かるが、人間が目視の手作業で作図する場合はどうしても精確性に欠けるので、不安なら複数本引いてもいい。

あと、左右それぞれの距離点を出した方がいい。距離点を複数用意した方が、このあと描く円をより精確にできる。

正方形の対角線は2本引けるので、画面に映る正方形が一つだけだとしても最低左右1本ずつは必ず引ける。

45度の線と消失線との交点を求める。そこが距離点。
左右の距離点が作れたら、視心を中心として両方の距離点を通る円を描く。これが90度視円錐の底面となる。

説明してなかったんですが、画面外まで作図が必要なのでキャンバスがゲーム画面いっぱいの状態を作業を開始しない方がいいです。今更！

ここで視心を中心とした円を描いたとき、円の半径をどう調整しても左右両方の距離点が円周上に乗らない場合、距離点の作図がズレていることになる。
距離点が1つだけだとこういう精確性チェックができないので2つあった方がいい。

精確な円が描けたら視点を書き込む。
視心から垂直および水平に線を伸ばしたときの、円との交点が視点です。その線は消失線として序盤ですでに書いているはず。

あとは各視点から画面の端に向かって線を引けば、視野の角（∠）が画面上に表れます。

編集ソフト内に角度を指定して直線を回転させられるようなツールがあれば、作図によって角度も自動的に分かるはず。そうでなければ他の方法で角度を測る必要があるが、最悪分度器を画面に当てれば測れる…

上記画像の場合、
垂直視野は上にも下にも27.5度なので、合わせて55度。
水平視野は左にも右にも42.78度なので、合わせて85.56度。

視心が真ん中であれば、上と下および左と右で角度が変わることはないので、分けて調べる必要は無い…。これはただの俺の測り方の都合です。
もし視心が真ん中じゃない場合は、上と下および左と右で角度が変わります。

マインクラフトの場合

マイクラは視野をゲーム内で自由に数値設定できるので、画面から測る意味はぶっちゃけ無い。
ただし、マイクラの場合はゲーム内設定で例えば「視野：70.00度」とだけ書いてあり、
これが垂直視野なのか水平視野なのかが分からないので、それを突き止めるために測る、という意義はあるかもしれない…。