
Unityのエッジコライダー2DをC++でオマージュしてみる。 作成編 その2
はじめに
前回は
「Unityのエッジコライダー2DをC++でオマージュしてみる。
作成編 その1」
を投稿しました
今回は前回からのつながりが大きいため、まだ未読の方は先に
前回を読んでみることをお勧めします
そして今回は、コライダーの重なりを完成させます
多少の制約のあるものにはなりますが
それなりに扱える関数になりました
それではさっそく見ていきましょう
Intersect関数の作成(アルゴリズムの思案 その2)
前回の失敗を踏まえて新たな案を考えてみました
今度は、「線」と「線」に目を向けます
先ほどまでは次のように「線」と「点」を見てました

ここから「線」と「線」に向けると次のように考えました
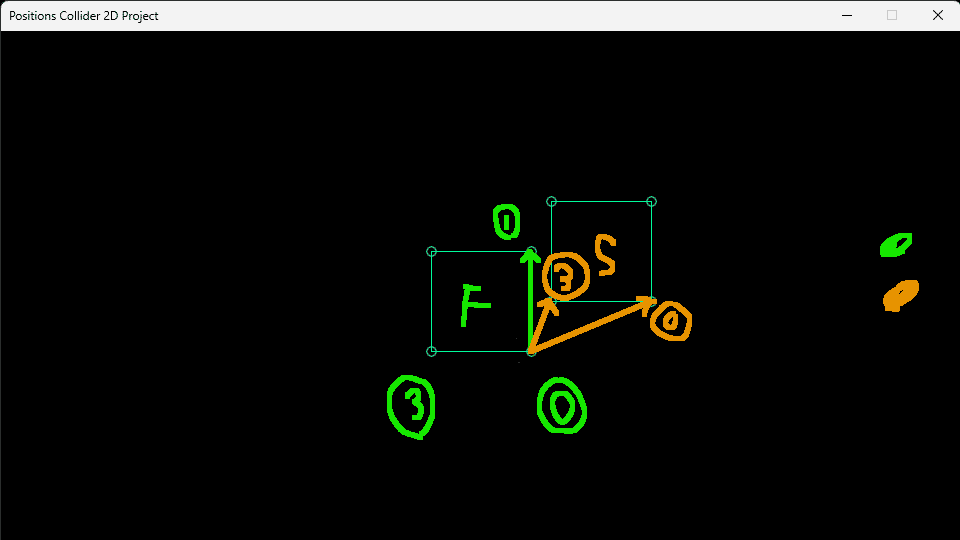
このように見ることにより、グリーンベクトルに対する
2つのベクトル情報を見比べることが可能になり
線と線の重なりを調べることができます
ですが、このコライダーには幾分かの問題があります
それは、線が重なっていないと重なっているかが調べられないことです
その解決が可能だったのが前回のアルゴリズムだったのですが
このコライダーでは、前提としてコライダー同士は
重なった状態ではじまらないことが重要な事項になってきます
それでは、処理の流れを書いていきます
まず、コライダーCFとCSを宣言します
今回も、緑色の数字はコライダーCFのインデックスを
オレンジ色の数字はコライダーCSのインデックスを表します

そしたら
CFのm_positions[3]からm_positions[0]へのベクトルGVectorに対しての
CFのm_positions[3]からCSのm_positions[3]へのベクトルのOVector1と
CFのm_positions[3]からCSのm_positions[0]へのベクトルのOvector2の
角度の差分をそれぞれ調べます
このとき、ふたつの差分が異なる正負ではない場合は
重なっていないということになる
今回は、差分が同じ正負なため
ふたつの線
CFのm_positions[3]からm_positions[0]と
CSのm_positions[3]からm_positions[0]は
重なっていないことがわかる

次は
CFのm_positions[3]からm_positions[0]と
CSのm_positions[0]からm_positions[1]を調べます
今回も差分の正負が同じなため
重なっていませんが
もう一つの重なっていない条件として
OVector1とOVector2の両方大きさが
GVectorの大きさを超えているため
重なっていません

その次は、上記と同じ理由で重なっていません

こちらも、重なっていません
今回は、ここまで調べてCFのm_positions[3]からm_positions[0]の
重なりの調査が完了します
次は、CFのm_positions[0]からm_positions[1]になります

こちらは
OVector1とOVector2の両方大きさが
GVectorの大きさを超えておらず
それぞれの差分の正負が異なるため
重なっています
今回は、重なりのみを調べる関数のため
この結果を出力した時点で
重なっているという結果を返します
以上がこのアルゴリズムの処理の流れになります
ちなみに、もし重なっていない場合は最後まで処理が進むため
できうる限りそうならないための対策も考えてます
ではの処理の流れを一度、まとめてみましょう
1.2つのコライダーをCFとCSに定める
2.もし、CFとCSのふたつのもっとも遠いm_positionsまでの距離の合計が
CFからCSまでの中心座標の距離よりも小さかったら
CFとCSは重なっていないとして処理を終了
3.ループi iを0で定義 この番号に再度戻った場合はi = i + 1する
もし、iがCFのm_positionsの要素数サイズ以上だったら
ループiを抜けて、9.に進む
4.CFのm_positions[i - 1]からm_positions[i]までを
GVectorと定義
5.ループj jを0で定義 この番号に再度戻った場合はj = j + 1する
もし、jがCSのm_positionsの要素数サイズ以上だったら
ループjを抜けて、3.に戻る
6.CFのm_positions[i - 1]からCSのm_positions[j - 1]までを
OVector1と定義
7.CFのm_positions[i - 1]からCSのm_positions[j]までを
OVector2と定義
8.もし、OVector1と2の両方の大きさがGVectorよりも大きくなく
かつ、GVectorとOVector1、GVectorとOVector2のそれぞれの
角度の差分の正負が異なる場合
CFとCSは重なっているとして処理を終了
9.5.へ戻る
10.CFとCSは重なっていないとして処理を終了
では、実際に作成してきたのでテストをしていきましょう
Intersect関数の作成(アルゴリズムのテスト その2)
一新したコードは以下のようになりました
PositionsCollider2D.cpp
/// <summary>
/// 重なり判定
/// </summary>
/// <param name="_collider">コリジョン</param>
/// <returns>ture = 重なっている : false = 重なっていない</returns>
bool PositionsCollider2D::Intersect(const PositionsCollider2D& _other)
{
// ふたつのコライダーのもっとも遠いm_positionsまでの距離の合計を求める
float VectorSumRange = m_LonghVector.range + _other.GetLongVector().range;
// 実際のふたつのコライダーの中心座標の距離を算出
float TransformRange = m_transform.GetPosition().MeasureUpTo(_other.GetPosition());
// もし、実際の距離が離れている場合の早期リターン
if (TransformRange > VectorSumRange) return false;
// _otherの座標の集合を取得
vector<Position2D> otherPositions = _other.GetPositions();
for (int i = 0; i < m_positions.size(); i++)
{
// i - 1が0未満の場合は、配列の最後列に設定
int iBack = i - 1;
if (iBack < 0)
iBack = m_positions.size() - 1;
// m_positions[i - 1]からm_positions[i]までをGVectorと定義
Vector2D GVector(m_positions[i] - m_positions[iBack]);
for (int j = 0; j < otherPositions.size(); j++)
{
// j - 1が0未満の場合は、配列の最後列に設定
int jBack = i - 1;
if (jBack < 0)
jBack = otherPositions.size() - 1;
// m_positions[i - 1]からotherPositionsのm_positions[j - 1]までをOVector1と定義
Vector2D OVector1((_other.GetPosition() + otherPositions[jBack]) - (GetPosition() + m_positions[iBack]));
// m_positions[i - 1]からotherPositionsのm_positions[j]までをOVector2と定義
Vector2D OVector2((_other.GetPosition() + otherPositions[j]) - (GetPosition() + m_positions[iBack]));
// OVector1と2の両方の大きさがGVectorよりも大きくなかったら
if (GVector.range < OVector1.range || GVector.range < OVector2.range)
{
//かつ、GVectorとOVector1、GVectorとOVector2のそれぞれの角度の差分の正負が異なる場合
if (OVector1.angle - GVector.angle > 0.f && OVector2.angle - GVector.angle < 0.f)
{
// ふたつのコライダーを重なっているとして処理を終了
return true;
}
if (OVector1.angle - GVector.angle < 0.f && OVector2.angle - GVector.angle > 0.f)
{
return true;
}
}
}
}
return false;
}さっそく表示させます。

うん?なにが問題なのでしょうか……
とりあえず、記述ミスを見つけました
int jBack = i - 1;
jBackと記載しているのにi - 1を得ようとしていますね
これでも問題は解決していませんね……
// OVector1と2の両方の大きさがGVectorよりも大きくなかったら
if (GVector.range < OVector1.range || GVector.range < OVector2.range)
この部分の条件式が間違っていたことに気が付きました。
いやはや、お恥ずかしい
改めて、表示テストを続行します




うーん、なるほど……
前回の失敗に通づる問題ですね
ですが、前回と違う点はまだ改善の余地があるということです
3つのベクトルがあるのです
まだ、あきらめるには早いでしょう
Intersect関数の作成(アルゴリズムの改善 その2)
おそらく、判断条件が薄かったのが原因として見ています
一度、わかりやすくするために一部の処理を別のクラスにします
新しくLineCollider2Dというクラスを作成しました
こちらは文字通り、線状のコライダーで
始点と終点の属性を持つクラスになっています
LineCollider2D.h
/**
* @file LineCollider2D.h
*
* @brief 線形コライダーのヘッダファイル
*
* @author CatCode
*
* @date 2024/12/15
*/
#pragma once
#include "Geometry2D.h"
/// <summary>
/// 2次元線形コライダークラス
/// </summary>
class LineCollider2D
{
private:
Position2D m_StartPosition;
Position2D m_GoalPosition;
public:
/*メインシステム*/
LineCollider2D() = default;
LineCollider2D(const Position2D& _StartPosition, const Position2D& _GoalPosition);
~LineCollider2D() = default;
bool operator==(const LineCollider2D& _line) const;
bool Detection(const LineCollider2D& _other) const;
/*設定/取得*/
void Set(const Position2D& _StartPosition, const Position2D& _GoalPosition);
};LineCollider2D.cpp
/**
* @file LineCollider2D.cpp
*
* @brief 線形コライダーのソースファイル
*
* @author CatCode
*
* @date 2024/12/15
*/
#include "LineCollider2D.h"
#include <utility>
/// <summary>
/// コンストラクタ
/// </summary>
/// <param name="_StartPosition">始点</param>
/// <param name="_GoalPosition">終点</param>
LineCollider2D::LineCollider2D(const Position2D& _StartPosition, const Position2D& _GoalPosition)
: m_StartPosition{ _StartPosition }
, m_GoalPosition { _GoalPosition }
{
}
/// <summary>
/// 線形コライダーとの衝突判定
/// </summary>
/// <param name="_line">外部の線形コライダー</param>
/// <returns></returns>
bool LineCollider2D::operator==(const LineCollider2D& _line) const
{
// 自身の線からVectorを生成
Vector2D thisVector{ m_GoalPosition - m_StartPosition };
// 自身の始点から外部の線の始点と終点へのVectorを生成
Vector2D otherVectorA{ _line.m_StartPosition - m_StartPosition };
Vector2D otherVectorB{ _line.m_GoalPosition - m_StartPosition };
// 外部の線からVectorを生成
Vector2D otherVector{ _line.m_GoalPosition - _line.m_StartPosition };
// 外部の始点から自身の線の始点と終点へのVectorを生成
Vector2D thisVectorA{ m_StartPosition - _line.m_StartPosition };
Vector2D thisVectorB{ m_GoalPosition - _line.m_StartPosition };
// 外積を使った交差判定
float cross1 = thisVector.Cross(otherVectorA);
float cross2 = thisVector.Cross(otherVectorB);
float cross3 = otherVector.Cross(thisVectorA);
float cross4 = otherVector.Cross(thisVectorB);
if (cross1 == 0.0f && cross2 == 0.0f && cross3 == 0.0f && cross4 == 0.0f)
{
// 共線の場合、線分の範囲が重なるか確認
return !(std::max(m_StartPosition.x, m_GoalPosition.x) < std::min(_line.m_StartPosition.x, _line.m_GoalPosition.x) ||
std::min(m_StartPosition.x, m_GoalPosition.x) > std::max(_line.m_StartPosition.x, _line.m_GoalPosition.x) ||
std::max(m_StartPosition.y, m_GoalPosition.y) < std::min(_line.m_StartPosition.y, _line.m_GoalPosition.y) ||
std::min(m_StartPosition.y, m_GoalPosition.y) > std::max(_line.m_StartPosition.y, _line.m_GoalPosition.y));
}
// 線分が重なる条件を確認
return (cross1 * cross2 < 0.0f) && (cross3 * cross4 < 0.0f);
}
/// <summary>
/// 線形コライダーとの衝突判定
/// </summary>
/// <param name="_other">外部のコライダー</param>
/// <returns></returns>
bool LineCollider2D::Detection(const LineCollider2D& _other) const
{
return (*this) == _other;
}
/// <summary>
/// 設定
/// </summary>
/// <param name="_StartPosition">始点</param>
/// <param name="_GoalPosition">終点</param>
void LineCollider2D::Set(const Position2D& _StartPosition, const Position2D& _GoalPosition)
{
m_StartPosition = _StartPosition;
m_GoalPosition = _GoalPosition;
}線と線同士の判定はの線形コライダーに任せて
再度、コードを練り直してみました
PositionsCollider2D.cpp
/// <summary>
/// 重なり判定
/// </summary>
/// <param name="_collider">コリジョン</param>
/// <returns>ture = 重なっている : false = 重なっていない</returns>
bool PositionsCollider2D::Intersect(const PositionsCollider2D& _other)
{
// ふたつのコライダーのもっとも遠いm_positionsまでの距離の合計を求める
float VectorSumRange = m_LonghVector.range + _other.GetLongVector().range;
// 実際のふたつのコライダーの中心座標の距離を算出
float TransformRange = m_transform.GetPosition().MeasureUpTo(_other.GetPosition());
// もし、実際の距離が離れている場合の早期リターン
if (TransformRange > VectorSumRange) return false;
// _otherの座標の集合を取得
vector<Position2D> otherPositions = _other.GetPositions();
for (int i = 0; i < m_positions.size(); i++)
{
// i - 1が0未満の場合は、配列の最後列に設定
int iBack = i - 1;
if (iBack < 0)
iBack = m_positions.size() - 1;
// m_positions[i - 1]からm_positions[i]までを線形コライダーと定義
LineCollider2D thisLine{ m_positions[iBack], m_positions[i] };
for (int j = 0; j < otherPositions.size(); j++)
{
// j - 1が0未満の場合は、配列の最後列に設定
int jBack = j - 1;
if (jBack < 0)
jBack = otherPositions.size() - 1;
// m_positions[i - 1]からotherPositions[j]までを線形コライダーと定義
LineCollider2D otherLine{ otherPositions[jBack], otherPositions[j] };
// もし線が衝突していたらふたつのコライダーは重なっているとして処理を終了
if (thisLine.Detection(otherLine))
return true;
}
}
return false;
}ついでにCFに座標を一つ追加して
テストしましょう

……ダメみたいですね
そしたら、次は重なる際の値を調べましょう


これらをもとに関数グラフで図にしてみました

バッチリ重なってますね……
どうやら私は初歩的な間違いを起こしていたようです
m_positionsはコライダーの中心座標からのベクトル
そして、この行……
// m_positions[i - 1]からotherPositions[j]までを線形コライダーと定義
LineCollider2D otherLine{ otherPositions[jBack], otherPositions[j] };中心座標からの数値になっていない!
修正し、再度テスト表示します




パーフェクト!!
これにて、Intersect関数の作成が終了します
まだ、潜在的な問題はありそうですが形になりました
とりあえず、ここまでのコードをAIでブラッシュアップして
休憩をはさみましょう
おわり
今回は
「Unityのエッジコライダー2DをC++でオマージュしてみる。
作成編 その1」
を書きました
Intersect関数の作成はなかなかに大変でした
先週に投稿したかったのですがこの関数が
ギリギリ完成していなかったので投稿できませんでした
それと、前回から出てきた制約ですが
それはコライダーの正常動作の前提条件が
コライダーの内側にコライダーが入っていない状況
ということのみです
その解決策が前回の思案なのですが
まずはこのコライダーの完成を目指す方針なので
このままコライダーの衝突処理の作成に入ります
次回は
「Unityのエッジコライダー2DをC++でオマージュしてみる。
作成編 その3」
です
乞うご期待!
それでは、良い一日になることをお祈りします……
