
指数関数は「うなぎのぼり」
今日、わたしんちの猫が、指数関数的に増えた。
というときの指数関数ってなんでしょう?
2の2乗は 2 ^ 2 = 4です。2の3乗なら 2 ^ 3 = 8ですね。
このように、ある定まった定数のナントカ乗で増えていく関数を「指数関数」とよびます。つまり、 x を変数とするときに、
![]()
…などが指数関数の例です(※通常は後者のことで、ただし e は後述する便利な定数)。2や e というのが「ある定まった定数」です。グラフを描けば、
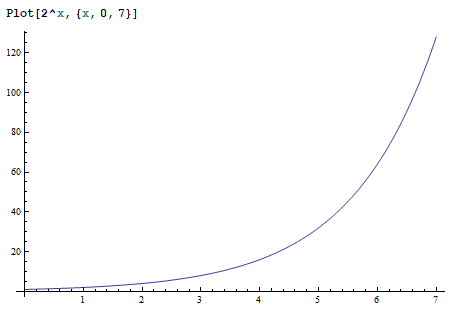
のようになります。この図は y = 2 ^ x を描いたものです。
指数関数の特筆すべき性質としては、変数 x の値(よこ軸)が 1、2、3、4、… と増えるごとに、関数の値(たて軸)のほうは 2、4、8、16、… のように倍々ゲームで増えていくということです。もし 3 ^ x ならば、“3倍3倍ゲーム”で増えていくことになります。
(ハイパー)インフレは指数関数的な例
指数関数的といえる現象の例として、2006年ごろから2009年にアフリカのジンバブエで起きた猛烈なインフレは有名です:
前月比796億%のインフレを経験したジンバブエで悲劇再来 | 金融市場異論百出 | ダイヤモンド・オンライン (2019.8.29付)
一定期間のインフレ率(というかインフレ倍率) R が変わらないとき、 x 期間後のモノの価格は、 R を x 回かけたもの、つまり R ^ x 倍となります。ですから倍率 R が1より大きいと(つまりデフレの逆ならば)、モノの価格≒物価は“ R 倍 R 倍ゲーム”で高くなっていくので、 R が大ならば結果が簡単に「うなぎのぼり」になってしまうのです。
一連のハイパーインフレーションと幾度ものジンバブエ・ドルの改革によって、ジンバブエ準備銀行のゴノ総裁は、2009年イグノーベル数学賞を受賞した。理由は「1セント~100兆ジンバブエ・ドルという幅広いお札を印刷することで、日々簡単にできるトレーニングを提供し、国民が非常に大きな数字にも対応できるようにしたから」。 (Wikipedia「ジンバブエ・ドル」項より筆者改変)
【2020年7月24日追記:正確に言うと、ハイパーインフレは2重指数関数と呼ばれるような激しい物価上昇であり、通常のインフレと区別しなくてはならないようです。くわしくは次のエントリーをお読みください → ハイパーインフレは“超指数関数的”(かのわさび) 】
なお2018年の日本の年間インフレ率は1.2%でした。
この数値は R = 1.012 ということですから、仮にそのまま10年たつと 1.012 ^ 10 = 約1.126倍です。つまり「10年で1割強の物価上昇」という適度な?インフレを意味していますので、ご安心ください。(デフレ脱却してたよね…。)
しかし、倍率が高くなかったとしても、指数関数は指数関数です。100年後まで計算してみれば、物価は約3.3倍にまでなります。
身近なところに、じつはひそんでいます
さて指数関数というのは、表計算ソフトのEXCELや、iPhoneの電卓にも標準で入っています。
エクセルならば「=EXP(数値)」という関数。
iPhoneなら、電卓を起動して画面を横向きにすると出てくる関数電卓に「e ^ x 」というボタンがあります(※下図中央上から2段目、なお画面回転を許可する必要あり)。
![iPhoneの関数電卓20200416 image0[1698]](https://assets.st-note.com/production/uploads/images/23089701/picture_pc_e4551f44f7401c287031cabd338fce53.png?width=1200)
エクセル関数のEXPという名前は、「exponential」(エクスポネンシャル)の略であり、ようは(急激に増加/減少する)指数関数のこと――ただし e ^ x の場合を指します。この「e」はある決まった定数のことで、「自然対数の底」とか「ネイピア数」とよばれるものです。その値は e = 2.7182818... 。
※ なぜこのような定数が登場し、頻繁に使われるのかについては、高校の数学教科書で「極限」や「微分」の章などを見ていただくとして、お手元の関数電卓では「 e ^ x 」や「e」のボタンを押したりすれば、この数が出ることをお確かめください!
まとめ
指数関数とは、倍々ゲームのようにして急激にうなぎのぼっていくタイプの関数のこと。一定の倍率で増加(または減少)していくというのがポイントです。その倍率は3倍でもいいし、1.012倍でもいいし、0.8倍でもいいし、n倍でもe倍でも、なんでも可です。※倍率が1より小さいときには、「うなぎ下がる」と気づいたあなたは、すばらしい!
そして一定の倍率とは限らないときでも、倍々ゲームに似た増減をする現象なら「指数関数的」というのです。
さて、身近にもそのような現象が潜んでいませんか? ぜひ頭を絞って、いろいろな例を探してみてください。
(解答例: 複利の定期預金。「一粒万倍」の米や豆。ポケットの中のビスケット。不都合な腹肉の細胞分裂。科学でいえば、宇宙創成期の空間膨脹などなど。逆に急減少していく現象もあることでしょう。)
以上かのわさびでした。またお会いしましょう!
いいなと思ったら応援しよう!

