
RとPythonでカルマンフィルタ
はじめに
気象予報士なら一度は聞いたことがあるカルマンフィルタ。気象予報士試験にも出題されます。そう、あの気温ガイダンスに使われているやつです。
ではどんなものかというと、数値予報モデルの系統誤差を学習して補正する手法、というくらいの理解ではないかと思います。実際、データサイエンスを学ぶまで私もその程度の理解でした。
そこでこのnoteでは、実際に自分でカルマンフィルタを使って太陽光発電予測をやってみた時の体験と、どういうツールを使ったかコードも少し交えて書きたいと思います。
※コードとデータの一部をGitHubに公開しています。
気象予測ではどういう問題設定にしているか?
カルマンフィルタは、時系列データに適用する統計モデリングの一種である状態空間モデルにおいて、「状態」を推定するための計算方法です。状態空間モデルとカルマンフィルタの概要は馬場真哉さんのサイト『Logics of Blue』や著書をご参照さい。私もこれで学んだので。
さて以前の私のイメージでは、カルマンフィルタは気温や発電量などを正確に予測するため、数値予報で計算された気象要素で回帰式を作って、その回帰係数を直近のデータで逐次更新していくというものでした。気温の場合、このような式になります。

左辺は求めたい気温の予測値、右辺は数値予報で計算された気象要素を使った回帰式です。この回帰係数を逐次更新するのがカルマンフィルタというイメージでした。
さて状態空間モデルは簡単に言うと、直接観測できない『状態』を、直接『観測』したデータで推定するというものです。
では上記の気温予測を状態空間モデルの概念に当てはめようとすると、ちょっと混乱します。なぜなら求めたい『状態』も直接する『観測』も、実際の気温そのものです。すると実際の気温だけで状態空間モデルが完結してしまい、数値予報の予測値が登場しようがなくなります。さて困った…
解決の糸口になりそうなのが、外生変数を組み込むという方法。実際の気温の説明変数となる数値予報の気象要素を、モデルに組み込みます。このとき回帰係数を、時間によって変化する「時変係数」として扱うことができるらしいのです…
…あれ?これって以前からイメージしていたカルマンフィルタの形そのものですよね。
ここでやっと気づきました。状態空間モデルにおける直接観測できない『状態』を、求めたい実際の気温そのものじゃなくて、数値予報の気象要素からなる回帰式の回帰係数としたら良いのではないか?そして『観測』した気温と、上記回帰式で推定した気温との誤差を、カルマンフィルタでフィードバックして回帰係数を更新しているのではないか?
こう考えると実装することができそうな気がしてきました。
後で調べてわかりましたが、気象庁の気温ガイダンスでもこのような問題設定でカルマンフィルタを実装しています。考え方はこれで大丈夫そうです。
(参考資料:数値予報課報告・別冊第64号:ガイダンスの解説)
RのKFASで実装
では実際に実装例をご紹介します。ここでは気温ではなくて、太陽光発電量を目的変数とします。そして説明変数は気象庁数値予報モデルMSMが予測した日射量・気温を使います。ここで日射量は太陽光発電量を支配する要素であることは当然として、気温は太陽光パネルの表面温度に関わる要素として取り入れています。一般に太陽光パネルの表面温度が高くなると、発電効率が悪くなります。
インプットにはこのようなデータを用意しています。
validtime power_sum DSWRF_SFC TMP_SFC
2019-01-01 12:00:00 28.4 524.225 4.35
2019-01-02 12:00:00 25.2 505.125 6.52
2019-01-03 12:00:00 26.3 459.950 4.60
2019-01-04 12:00:00 28.8 530.890 4.69
2019-01-05 12:00:00 28.2 519.005 11.77
2019-01-06 12:00:00 26.5 401.090 4.03
...左から対象時刻、発電量実績値、MSM日射量予測値、MSM地上気温予測値となっています。また12時のデータを1年分用意しています。
Rで実装するにはKFASパッケージを使用します。KFASを使ったコードの書き方は、詳細はやはり馬場真哉さんのサイト『Logics of Blue』や著書をご覧下さい。ここではモデルの構造を決める部分のコードのみを掲載します。
# step1 : モデルの構造を決める
model <- SSModel(
H = NA,
power_sum ~
SSMregression( ~ DSWRF_SFC + TMP_SFC, Q = diag(rep(NA, 2)) ),
data = train
)
# step2 : パラメタ推定(2度行なった方が良かった)
model.tmp <- fitSSM(model, inits = rep(1, 3))
model.fit <- fitSSM(model, inits = model.tmp$optim.out$par)
# step3,4 : フィルタリング、スムージング
model.result <- KFS(
model.fit$model,
filtering = c("state", "mean"),
smoothing = c("state", "mean")
)外生変数による回帰を表現するため、SSMregressionだけを使っています。計算結果の一部を表示します。
(Intercept) DSWRF_SFC TMP_SFC
[361,] -0.9499304 0.03711975 0.3524265
[362,] -0.9554264 0.03791211 0.3525241
[363,] -0.8614913 0.03881518 0.3456236
[364,] -0.7886169 0.03950150 0.3404230
[365,] -0.9409188 0.03959059 0.3457278
[366,] -0.9653778 0.03980350 0.3471211日射量の回帰係数の推移をグラフ化してみます。最初は暴れてますが、徐々に一定の範囲に落ち着いています。まあ何となく良さそうです。
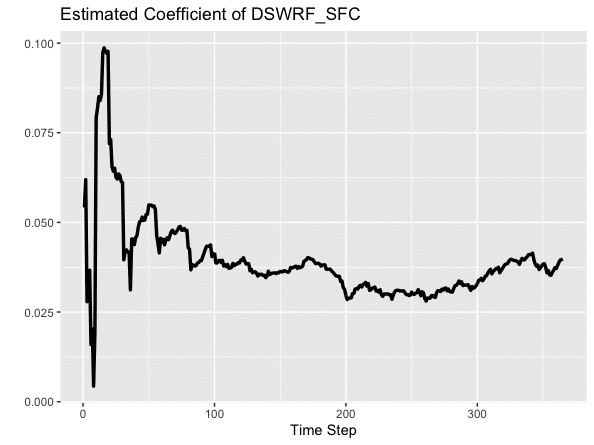
逐次更新はどうやる?
なんとなくできたっぽいんですが、ただよくわからない点もあって、手元のデータで一旦モデリングした後、翌日に新しいデータが入ったときにどうやって学習の続きを進めるのか?
私が調べた限りだとKFASパッケージはそういう使い方には対応してなくて、新しいデータも加えてゼロからモデリングし直すしかない…のだと思います、たぶん。計算はほぼ一瞬で終わるのでそれでも良いのかもしれませんが、どうにも気持ち悪い。
これについて詳しい方、ご教示いただけると嬉しです。
Pythonのstatsmodelで実装
次はPythonです。Pythonの場合はstatsmodelを使って状態空間モデルを記述することができます。これも詳細は馬場真哉さんのブログを参照して下さい。ここでは私が試したコードのみ載せます。
# ローカルレベルモデルの推定
ssm = sm.tsa.UnobservedComponents( train["power_sum"], level = 'local level',
exog = train[["DSWRF_SFC","TMP_SFC"]])
# 最尤法によるパラメタの推定
ssm_fit = ssm.fit(
method='bfgs',
maxiter=500,
start_params=ssm.fit(method='nm', maxiter=500).params,
)
# 推定されたパラメタ一覧
print(ssm_fit.summary())statsmodelの場合は、ローカルレベルモデルにした上で外生変数をexogオプションで加える、という形の記述にするようです。何だか自由度低そう、と思っていたら案の定でした。以下が出力の一部なのですが…
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------------
sigma2.irregular 74.7485 5.868 12.739 0.000 63.248 86.249
sigma2.level 0.1319 0.105 1.256 0.209 -0.074 0.338
beta.DSWRF_SFC 0.0371 0.003 13.927 0.000 0.032 0.042
beta.TMP_SFC 0.2093 0.134 1.560 0.119 -0.054 0.472最後の2行を見ると、日射量と気温の回帰係数が表示されているような。どうやら外生変数として与えた説明変数の回帰係数は、時変係数じゃなくて固定値が1つ求まるだけのようです。これではやりたかったモデリングになりませんね…
ということで、私の調べた限りでは、statsmodelではイメージしてたカルマンフィルタの実装はできないようです。
もしくは、自分でスクラッチで実装という手もあります。実際カルマンフィルタの部分だけならできそうなんですが、パラメータの推定(過程誤差・観測誤差の分散の最尤推定)をスクラッチ実装は結構大変そう。ここだけでもライブラリが使えるといいのですが…この点も詳しい方ご教示いただけると嬉しいです!
最後まで読んでいただき、ありがとうございました。
