さるぶつ道場 速度と加速度1解答

斜面上での斜方投射

　問題はこちらです．

　重力加速度を $${x}$$ 軸，$${y}$$ 軸のそれぞれの方向に分解して考えましょう．三角関数の処理に注意しながら，計算を進めてください．

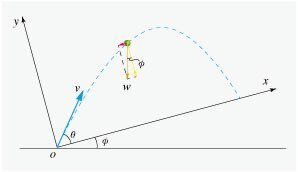
　図より，小球の $${x}$$ 軸方向，及び $${y}$$ 軸方向の運動方程式は，

$${ma_x=-m{\it g}\sin \phi}$$
$${ma_y=-m{\it g}\cos \phi}$$

　上の運動方程式より，小球の $${x}$$ 軸方向，及び $${y}$$ 軸方向の加速度は，

$${a_x=-{\it g}\sin \phi}$$
$${a_y=-{\it g}\cos \phi}$$

　小球の位置 $${(x,y)}$$ は，

　$${x=v\cos\theta\cdot t -\frac{1}{2}{\it g}\sin \phi\cdot t^2}$$  …　①

　$${y=v\sin\theta \cdot t-\frac{1}{2}{\it g}\cos \phi\cdot t^2}$$ …　②

　小球が斜面に衝突するとき，$${y=0}$$ なので②式より，

$${t=0, \frac{2v\sin\theta}{ {\it g}\cos \phi}}$$

　$${t>0}$$ なので，①式に$${t= \frac{2v\sin\theta}{ {\it g}\cos \phi}}$$ を代入して斜面に落下する点の座標 $${x_f}$$ を求めると，

$${ x_f = v\cos \theta\cdot\frac{2v\sin\theta}{ {\it g}\cos \phi}-\frac{1}{2}{\it g}\sin \phi\cdot \left(\frac{2v\sin\theta}{ {\it g}\cos \phi}\right)^2 }$$

$${x_f= \frac{2v^2\sin \theta (\cos  \theta\cos \phi -\sin\theta \sin \phi )}{ {\it g}\cos ^2 \phi}  }$$

$${x_f= \frac{2v^2\sin \theta \cos ( \theta +\phi )}{ {\it g}\cos ^2 \phi}}$$