
さるぶつ道場 熱5解答
立方体容器に封入された気体分子の運動
気体分子運動論の基本的な問題.④の答えはいつも同じであるが,導出する過程にはいくつかのアプローチがあるので,問題文をよく読んで題意にあわせて解く必要がある.①では,面に垂直な成分のみが変化することに注意すること.⑧,⑨は単原子分子理想気体の内部エネルギーの公式や,ボルツマン定数を思い出しながら解くとよい.
①

分子aは壁Sと弾性衝突するので,図2より,
$${{\boldsymbol v}'=(-v_x,v_y,v_z)}$$
②
分子aの衝突前の運動量は $${{\boldsymbol p}=(mv_x,mv_y,mv_z)}$$ ,衝突後の運動量は $${{\boldsymbol p}'=(-mv_x,mv_y,mv_z)}$$ なので,衝突前後の運動量の変化 $${\Delta p}$$ は,
$${\Delta {\boldsymbol p}={\boldsymbol p}'-{\boldsymbol p}=(-2mv_x,0,0)}$$
壁が受ける力積は $${{\boldsymbol I}=-\Delta {\boldsymbol p}}$$ なので,
$${{\boldsymbol I}=(2mv_x,0,0)}$$
壁Sが分子aから受ける力積の大きさ $${I}$$ は,
$${I=2mv_x}$$
③

図3より,
$${T_0=\frac{2L}{v_x}}$$
④
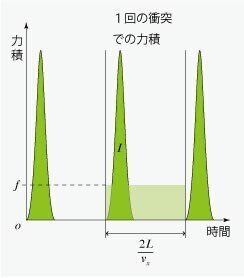
図4より,
$${f=\frac{I}{T_0}=\frac{mv_x^2}{L}}$$
⑤
速度の $${y}$$ 成分 ,及び $${z}$$ 成分 の2乗の平均をそれぞれ $${\overline{v_y^2}}$$ ,$${\overline{v_z^2}}$$ とすると,$${\overline {v_x^2}=\overline {v_y^2}=\overline {v_z^2}}$$ なので,
$$
\begin{array}{}
\overline {v^2}&=&\overline {v_x^2}+\overline {v_y^2}+\overline {v_z^2}\\
\overline {v^2}&=&3\overline {v_x^2}\\
\overline {v_x^2}&=&\frac{1}{3}\overline {v^2}
\end{array}
$$
⑥
$${N}$$ 個の分子が壁に及ぼす力の平均 $${\overline f}$$ は,
$${\overline f=\frac{m\overline {v_x^2}}{L}=\frac{m\overline {v^2}}{3L}}$$
したがって,$${N}$$ 個の分子が壁に及ぼす力の和は,
$${F=N\overline f=\frac{Nm\overline {v^2}}{3L}}$$
⑦
壁Sが受ける圧力は,
$${p=\frac{F}{L^2}=\frac{Nm\overline {v^2}}{3L^3}}$$
⑧
⑦より,
$$
\begin{array}{}
p&=&\frac{Nm\overline {v^2}}{3L^3}\\
N\cdot \frac{1}{2}m\overline {v^2}&=&\frac{3}{2}pL^3\\
U&=&\frac{3}{2}pL^3\\
\end{array}
$$
⑨
気体の物質量は $${n=\frac{N}{N_A}}$$ なので,気体の状態方程式は,
$$
\begin{array}{}
pV&=&nRT\\
pL^3&=&\frac{N}{N_A}RT
\end{array}
$$
⑧より,
$$
\begin{array}{}
U&=&\frac{3}{2}pL^3\\
NK&=&\frac{3}{2}\cdot \frac{N}{N_A}RT\\
K&=&\frac{3R}{2N_A}T\
\end{array}
$$
詳しい説明はこちらのブログか,下の動画を参考にしてください.
