
さるぶつ道場 波の基本的な性質1
壁で反射する縦波が作る定在波
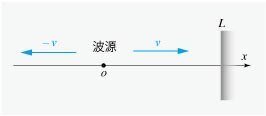
図1は,原点を波源として $${x}$$ 軸上を伝わる振幅 $${A}$$ ,振動数 $${f}$$ ,速さ $${v}$$ の縦波を横波表示したもので,$${y}$$ 軸は媒質の変位を表しており,波源から $${x}$$ 軸正の向きに進む波は $${y_1=A\sin 2\pi f\left(t-\frac{x}{v}\right)}$$ ,負の向きに進む波は $${y_2=A\sin 2\pi f\left(t+\frac{x}{v}\right)}$$ で表される.$${x=L}$$ には剛体の壁があり,波は反射して $${x}$$ 軸負の向きに進むが,波源は反射波に影響しないものとする.また,$${L}$$ は波長に比べて十分大きいものとする.
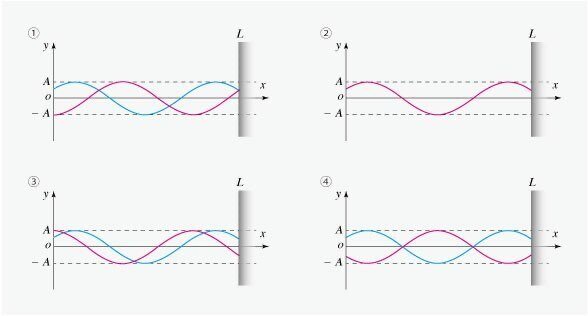
(1) $${0<x<L}$$ において,$${x}$$ 軸正の向きに進む波のある時刻の変位が図2のように表されるとき,反射波の変位はどのように表されるか.図3の選択肢①~④の中から選べ.

(2) 波源から $${x}$$ 軸正の向きへ進む波が,壁で反射した後に位置 $${x}$$ に達するまでの時間を求めよ.
(3) 壁で反射して負の向きに進む波を $${y_3=A\sin 2\pi f\left(t+\frac{x}{v}+\delta\right)}$$ としたとき, $${\delta}$$ を求めよ.
(3) $${0<x<L}$$ における入射波と反射波の合成波の変位 $${y_4}$$ は,$${y_4=y_1+y_3=}$$(あ)$${A\cos2\pi f}$$ (い) $${\sin 2\pi f}$$(う) で与えられる.(あ)~(う)に入る数式を求めよ.なお必要ならば下の公式を用いてよい.
$$
\begin{array}{}
\sin A+\sin B &=&2\sin \frac{A+B}{2}\cos \frac{A-B}{2}\\
\sin A-\sin B &=&2\cos \frac{A+B}{2}\sin \frac{A-B}{2}
\end{array}
$$
(5) $${0<x<L}$$ には常に変位が0の点がいくつかあった.変位が0の点のうち,壁に最も近い点の座標を求めよ.
(6) $${x<0}$$ における全ての点で,波の変位が0になるときの $${f}$$ を,自然数 $${m}$$を用いて表せ.
解答はこちらです.
