
さるぶつ道場 斜方投射2解答
斜面内での斜方投射
問題はこちらです.
斜面内の斜方投射なので,斜面に沿った方向( $${y}$$ 軸方向)には力がはたらきますが,水平成分( $${x}$$ 軸方向)は等速直線運動です.まず重力の斜面に沿った成分を考えるようにしましょう.その後は普通の斜方投射の問題と同じです.ただし,$${\theta}$$ と $${\phi}$$ を混同しないようにしましょう.また,問題文から条件を正確に読み取るようにしましょう.
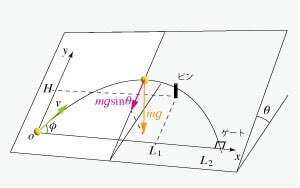
図3のように力は分解できるので,小球にはたらく $${x}$$ 軸方向の力は0,$${y}$$ 軸方向の力は $${-mg\sin\theta}$$ である.$${y}$$ 軸方向の運動方程式は,
$${ma_y=-mg\sin\theta}$$
したがって物体は, $${x}$$ 軸方向には初速度 $${v\cos\phi}$$ で等速直線運動,$${y}$$ 軸方向には初速度 $${v\sin\phi}$$ ,加速度 $${-g\sin\theta}$$ の等加速度直線運動をする.
小球を投げ出した時刻を0として,時刻 $${t}$$ での位置を表す式は,
$${x=v\cos \phi \cdot t}$$
$${y=v\sin \phi\cdot t-\frac{1}{2}g\sin \theta \cdot t^2}$$
①式より,小球が $${x=L_2}$$ に到達する時刻 $${t_0}$$ は,
$${t_0=\frac{L_2}{v\cos\phi}}$$
$${t=t_0}$$ のとき $${y=0}$$ なので,$${t_0}$$ を②式に代入して,
$${0=v\sin \phi\cdot \frac{L_2}{v\cos \phi}-\frac{1}{2}g\sin \theta \cdot \left ( \frac{L_2}{v\cos \phi} \right ) ^2}$$
$${v=\sqrt{\frac{gL_2\sin \theta }{\sin 2\phi}}}$$
小球がピンを越えるためには,小球が $${x=L_1}$$ に到達する時刻 $${t_1=\frac{L_1}{v\cos\phi}}$$ のとき,$${y>H}$$ でなければならない.
$${t_1}$$ ,及び $${v}$$ を②式に代入して,
$${H}$$<$${v \sin \phi\cdot \frac{L_1}{v\cos \phi}-\frac{1}{2}g\sin \theta \cdot \left ( \frac{L_1}{v\cos \phi} \right ) ^2}$$
$${H}$$<$${L_1\tan \phi -\frac{gL_1^2 \sin \theta}{2 v^2 \cos ^2 \phi}}$$
$${v=\sqrt{\frac{gL_2\sin \theta }{\sin 2\phi}}}$$ を代入して,
$${H}$$<$${L_1\tan \phi -\frac{gL_1^2 \sin \theta}{2 \left(\sqrt{\frac{{\text g}L_2\sin \theta }{\sin 2\phi}}\right)^2 \cos ^2 \phi} }$$
$${H}$$<$${L_1\tan \phi -\frac{{\text g}L_1^2 \sin \theta \sin 2\phi}{2 {\text g}L_2\sin \theta \cos ^2 \phi} }$$
$${H}$$<$${L_1\tan \phi -\frac{L_1^2 \tan \phi}{ L_2}}$$
$${H}$$<$${\left(\frac{L_1L_2 -L_1^2}{ L_2}\right) \tan \phi}$$
$${\tan \phi}$$>$${\frac{ L_2H}{L_1(L_2 -L_1)}}$$
