
さるぶつ道場 斜方投射3解答
加速する電車内での斜方投射
問題はこちらです.
慣性力により,水平方向にも加速度があることに注意しましょう.
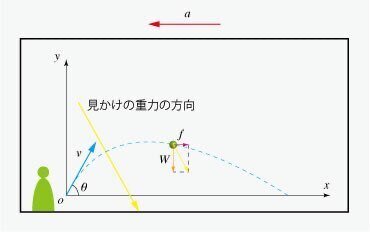
図のように,電車内では鉛直下向きの重力 $${W=mg}$$ に加えて,水平右向きに慣性力 $${f=ma}$$ がはたらく.運動方程式は,
$$
\begin{array}{}
ma_x&=&ma\\
ma_y&=&-mg\\
\end{array}
$$
運動方程式より,$${x}$$ 軸方向,$${y}$$ 軸方向の加速度は,
$$
\begin{array}{}
a_x&=&a\\
a_y&=&- g\\
\end{array}
$$
小球の位置は,
$$
\begin{array}{}
x&=&v\cos \theta \cdot t+\frac{1}{2}a t^2\ \cdots ①\\
y&=&v\sin \theta \cdot t-\frac{1}{2}gt^2\ \cdots ②\\
\end{array}
$$
小球が床に落下したとき $${y=0}$$ なので,②式より,
$${t=0,\ \frac{2v\sin \theta}{g}}$$
$${t>0}$$ なので,①式に $${t=\frac{2v\sin \theta}{g}}$$ を代入して,
$$
\begin{array}{}
x_{fallingpoint}&=&v\cos \theta \cdot \frac{2v\sin \theta}{g}+\frac{1}{2}a \left(\frac{2v\sin \theta}{g}\right)^2\\
&=& \frac{2v^2\sin \theta ({\text g}\cos \theta +a\sin \theta) }{g^2}\\
\end{array}
$$
詳しい説明はテキストを参考にしてください.
