
さるぶつ道場 剛体にはたらく力のつりあい1解答
水平に保った剛体棒の先端でばねを振動させたときの摩擦力
問題はこちらです.
(1)は「剛体が静止し続ける条件」を利用した基本的な問題です.「剛体が静止し続ける条件」の詳細はテキストを参考にしてください.
(2)では,P端に力を及ぼしているのは糸の張力とばねの弾性力であることに注意しましょう.また,(1)の結果より,棒を水平に保つための摩擦力はばねの状態にかかわらず,一定であることに注目してください.
「弾性力が大きくなると張力が大きくなる→張力が大きくなると垂直抗力が大きくなる→垂直抗力が大きくなると最大摩擦力が大きくなる」というように順序立てて考えるようにしましょう.
(1)図2のように,棒にはたらく重力を $${W}$$ ,おもりにはたらく重力を $${w}$$ ,点Pをばねが引く力を $${f}$$ とする.
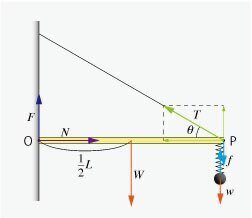
おもりはつりあいの位置で静止しているので,$${f=w=mg}$$ である.点Pのまわりの力のモーメントのつりあいより,
$${W\cdot \frac{1}{2}L-FL=0}$$
$${F=\frac{1}{2}Mg}$$
点Oのまわりの力のモーメントのつりあいより,
$${T\sin \theta \cdot L-W\cdot \frac{1}{2}L-fL=0}$$
$${T\sin \theta =\left(\frac{1}{2}M+m\right)g}$$
$${T=\frac{M+2m}{2\sin\theta}g}$$
水平方向の棒にはたらく力のつりあいより,
$${N-T\cos \theta =0}$$
$${N=\frac{M+2m}{2\tan\theta}g}$$
(2)おもりを鉛直下向きに $${\frac{1}{2}d}$$ だけ引いて静かに離しとき,おもりはつりあいの位置を中心に振幅 $${\frac{1}{2}d}$$ の振動をするので,P点をばねが引く力は $${\frac{1}{2}kd \leqq f\leqq \frac{3}{2}kd }$$ の範囲で変化する.弾性力 $${f}$$ に関わらず,(1)より棒と壁との間の摩擦力 $${F}$$ は変化しないので,図3のように鉛直方向の棒にはたらく力のつりあい $${F+T\sin \theta -W-f=0}$$ より,弾性力 $${f}$$ が大きくなると張力 $${T}$$ が大きくなる. $${T}$$ が大きくなると,水平方向の棒にはたらく力のつりあい $${N-T\cos \theta =0}$$ より垂直抗力 $${N}$$ が大きくなるので,棒がすべりやすくなるのは $${N}$$(最大摩擦力$${R_{Max}=\mu N}$$ )が最小となる $${f=\frac{1}{2}kd=\frac{1}{2}mg}$$ のときである.

このとき,点Oのまわりの力のモーメントのつりあいより,
$${T\sin \theta \cdot L-W\cdot \frac{1}{2}L-fL=0}$$
$${T\sin \theta =\frac{1}{2}(M+m)g}$$
$${T=\frac{M+m}{2\sin\theta}g}$$
水平方向の棒にはたらく力のつりあいより,
$${N-T\cos \theta =0}$$
$${N=\frac{M+m}{2\tan\theta} g}$$
棒がすべらないための条件は,$${R_{Max} \geqq F}$$ なので,最小値は $${F =\mu N }$$ のときである.
$${\mu N=F}$$
$${\mu \frac{M+m}{2\tan\theta} g=\frac{1}{2}Mg}$$
$${\mu=\frac{M\tan \theta}{M+m}}$$
