
さるぶつ牧場 円運動5解答
円錐振り子の周期
問題はこちらです.
張力の水平成分が等速円運動の向心力を担っていることに注目しましょう.また,水平面内で運動しているので,張力の鉛直成分と重力がつりあっていることにも注目しましょう.テキストでは遠心力を考えた,力のつりあいによる解法を掲載しています,興味のある人はブログも確認してください.
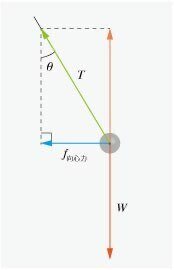
図1のように,張力の水平成分が向心力を担っているので,運動方程式は,
$${ma=T\sin \theta}$$
鉛直方向の力のつりあいを考えると,
$$
\begin{array}{}
T\cos \theta-mg&=&0\\
T&=&\frac{mg}{\cos \theta}
\end{array}
$$
半径は $${l\sin\theta}$$ なので,運動方程式は,
$$
\begin{array}{}
ml\sin \theta \cdot \omega ^2&=&\frac{m g}{\cos \theta}\sin\theta\\
\omega ^2&=&\frac{g}{l\cos \theta}\\
\omega &=&\sqrt {\frac{g}{l\cos \theta}}\\
\end{array}
$$
ゆえに,周期 $${T}$$ は,
$${T=\frac{2\pi}{\omega}=2\pi \sqrt {\frac{l\cos \theta}{g}}}$$
詳しい説明はこちらのブログか,下の動画を参考にしてください.
