さるぶつ道場 運動の法則6解答

粗い斜面を往復する物体の速さ

　問題はこちらです．

　この問いは，斜面を上る距離がわかれば解けます．距離を求めるために，運動方程式を立てて考えましょう．斜面を上るときと下るときで，図1のように動摩擦力の向きが反対向きになるので注意しましょう．

図1

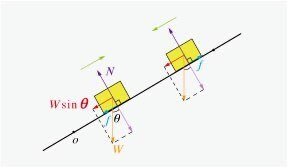
　物体の質量を $${m}$$ とすると，物体が斜面を登るときの加速度 $${a}$$ は，

$${ma=-mg\sin \theta -\mu mg\cos \theta}$$
$${a=-g(\sin \theta +\mu \cos \theta)}$$

　物体が斜面を下るときの加速度 $${a'}$$ は，

$${ma'=mg\sin \theta -\mu mg\cos \theta}$$
$${a'=g(\sin \theta -\mu \cos \theta)}$$

図2

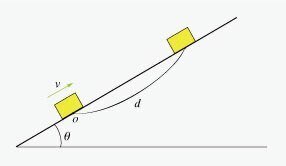
　図2のように，物体は距離 $${d}$$ だけ進んで折り返したとすると， $${v^2-v_0^2=2ax}$$ より上りは，

$${0^2-v^2=-2g(\sin \theta +\mu \cos \theta)d}$$
$${v^2=2g(\sin \theta +\mu \cos \theta)d}$$ …①

下りは，

$${v'^2-0^2=2g(\sin \theta -\mu \cos \theta)d}$$
$${v'^2=2g(\sin \theta -\mu \cos \theta)d}$$ …②

①，②式より $${d}$$ を消去すると，

$${\frac{v^2}{v'^2}=\frac{\sin \theta +\mu \cos \theta}{\sin \theta -\mu \cos \theta}}$$
$${v'^2=\frac{\sin \theta -\mu \cos \theta}{\sin \theta +\mu \cos \theta}v^2}$$
$${v'=\sqrt \frac{\sin \theta -\mu \cos \theta}{\sin \theta +\mu \cos \theta}v}$$
$${v'=\sqrt \frac{\tan \theta -\mu }{\tan \theta +\mu }v}$$

　ゆえに，$${\sqrt \frac{\tan \theta -\mu }{\tan \theta +\mu }}$$ 倍である．