OMC179参加記
過去の参加記や過去問でない記事は初めてになりますね。
本記事は2023/9/27 に開催されたOMC179(for beginners)の参加記になります。
チーム戦の方では、175~178で行った予選を通過することができたため、この回は決勝戦ということになります。OMC177の方でレートが1200以上になったため、今回はrate対象外ではありますが、チーム戦に参加していたことで、一定の緊張感を持って取り組めました。OMCに限らず、緊張への対策というのは(数学とはあまり関係がないですが)重要と思うので、ありがたく活用させてもらっています。
毎度注意書きさせてもらいますが、基本的に「参加中の動き」の部分は思考垂れ流しなので、口語調が混じりますが、何かを攻撃する意図はないです。
参加中の動き
前回のfor beginners同様、点数設定が少し高めなD,E,Fあたりから開いて、FAボーナスを狙う作戦で動きました。
D

ぱっと見で手を動かしたら何とかなりそうなDに着手することに。
とにかく変数を絞りたいので、cosxのみになるように式変形を行うと、
1/4(c+1)^2+1/(1+c)となって、後者を二つに分けると相加相乗の不等式が使えるとわかり、最小値3cbrt(1/16)とわかる(※1)
最小多項式はt^3 - 27/16なので、あとは電卓。
相加相乗をスムーズに使用できたので、目論見通り、FAをとることができた! 実はチームメイトのpomodorさんと衝突(※2)していたらしい。
ここで、EとFを見ると、Eがぱっと見ではよくわからない組み合わせ(ただ、マスに書き込む数の制約は強そう、というのはうかがえた)、Fは見た目がとてもシンプルな代数の問題だったので、計算で何とかなりそうなFへ。
F
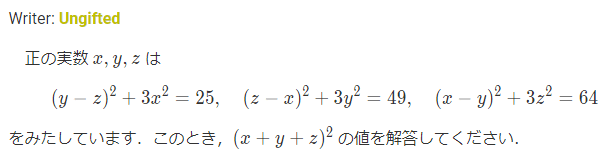
右辺がいい感じの平方数だし、cyclicな式だし、きっと模範解答はうまい幾何学的解釈をしているんだろうな、とは思ったものの、自分を天才だと思って発想が降ってくるのを待つとろくなことにならないので、とにかく計算でもがく。与式の差をみれば左辺がx-y,y-z,z-xとかで割れて少し見やすくなるということで、引いてみると 2(x+y+z)(x-y) = 24 と、(x-y)以外の項は共通の項になるような数字設定になっていることがわかる。しかも、x+y+zというのは問われている数値。これをtとおくと、
y-x = 12/t, z-y =15/(2t)という式を得て、y=12/t + x, z=15/(2t) + xと表せる。(y,zという変数を消す動き)
これをまずx+y+z=tに代入することで、x=1/3(t-63/(2t))となるため、x,y,zがすべてtのみで表せたことになる。
与式の一つ目の(y-z)^2+3x^2 = 25に代入することで解ける。方程式としてはt^2の二次方程式になる。
129以外に9という解もでてくるため、これを否定する必要があるが、コンテスト中は値が確定する上に、小さいほうは何らかの不等式で実数にならなくなるだろうとアテをつけて、129の方を提出。
(9の除外は、全問解いた後にやった。)
また、二次方程式の立式で一度計算を間違え、答えが整数にならなくなったので、落ち着くためにCやBを合間に解いていた。
C

(本題とはそこまで関係がないですが、アンケート結果で○○.〇%みたいなのを見たときに、分母がどれくらいなのか概算して、本当に信頼できるアンケートなのか吟味する、みたいなことをテレビなどを見て考えたりすることがあります。)
愚直に47.5 <= 100a/b <48.5 なる小さい正整数の組を探す。
カッコ内みたいなことをよく考えるのはもしかしたら結構+に働いたのかもしれない? とにかく、心を落ち着かせるにはよい問題だった。
B

四角形、といった指定がないので、長さの決まった針金をグニャグニャ動かす感覚でA,B,Cが共線、B,C,Dが共線のケースを考えればよい。
こちらも心を落ち着かせるにはよい問題であったが、Fを正答した後、解答を投げられていないことに気づき、大慌てで提出した。(提出して、間違っていたのかと勘違いした)
Eを解けない可能性を考慮して、とりあえずAへ。
A

abcd/bc = 15 (解説リスペクト)
これ、変数の種類とかけられている変数の数を増やすだけで割と非自明になったりしますよね。難問の1ステップとして出てきて意外と気づかない、みたいなことがありそう。
E

Eに集中する環境を作れたので、愚直でもよいから数え上げると覚悟。
Eに行く前に順位表をチラ見したところ、なんと2位につけていたため、より覚悟が強まった。
まず、前述したとおり、不等号の数からして、左上に0,右下に12を書くと、すべてのマスが一意に定まる(i+jごとに数値が決まる)ことがわかる。この状態を基本状態と呼ぶことにする。
一方で、使える数値は0~13であり、基本状態の各マスは不等号の制約から、増やせても高々1とわかる。
一方であるマスを基本状態から1増やしたときに、そのマスよりも右下にあるマスはすべて1増やさなければならない。
これらの制約と、基本状態でのすべてのマスの和は偶数になる(0,1を市松模様に書き込んでいる)ことから、「基本状態から1増やしたマス」が奇数個あることが必要十分で、言い換えると以下の数え上げ問題に帰着
0<=b1<=…<=b7<=7, b1~b7の和が奇数
c_i = 7-b_(8-i) という写像で偶数の{b_i}と奇数の{b_i}に1対1の対応ができるため、0<=b1<=…<=b7<=7となる整数を数えればよいが、これは14C7に一致。よって14C7/2が答え。
-そのマスより右下にあるマスはすべて1増やす について、複数マス選ぶことはできないと勘違いして1ペナ
-1<=b1 と勘違いして、1ペナ (13C7だとさすがに対称性がなさすぎるので気づくべきミス)
感想と反省
19分4秒で6問正解(2ペナ)で、なんと順位は2位でした!シルバーコレクターですね(※3)
Dで作戦通りFAが取れたり、苦手そうな分野のEがちゃんと解けたり、Fで作戦通りすぐ計算に走ったおかげで余計なことを考えずに済んだりして、かなり満足のいくパフォーマンスが出せました。
問題も面白いものがそろっていて、Fは模範解答ではやはり幾何学的解釈をしていたのですが、背景がよくわからない変換も入っていて、なかなか面白かったです。
反省点としては、ペナルティがもしなかったら(そんなことを言い出したらキリがないですが)、Fで計算沼らなければ、といったたらればで1位が取れていたかもしれない、というところでしょうか。以前の2位の時は1位は遠い印象でしたが、今回は一番近づけたかなと思います。
実際にはexpert以外の回では猛者が参加していなかったりするため、順位に絶対的な価値があるかといわれると少し微妙なところですが、よいパフォーマンスを出せてとてもうれしいです。
チーム戦の方も優勝できたので、思い出に残る回になりました。
※1 等号成立条件は無視しました。最近そんな話が話題になってましたね。
※2 pomodorさんもDのFAを狙って、自分と11秒差で通していたようです。チーム内での熾烈な争い
※3

