【アッセイを考える #6】必要なサンプル数はいくつ？

　「アッセイを考える」シリーズの6回目である。前回はハイスループットな定量試験で用いられるウェルプレート上で発生するグラデーションの実情とその原因探索について深堀りしてみた。

　今回は、定量試験の延長として、アッセイのサンプル数（$${N}$$ 数）に着目してみようと思う。盲目的に $${N}$$ = 3 でやってみることもよくやるが、それで不十分な場合もある。一方で、無限にサンプル数を稼ぐことはできるわけでもないので、目的に合わせた試験デザインが必要となる。

【問題6】
　細胞Xは物質Aを多く生産することが知られており、物質Aの生産量が多ければ多いほど「良い」細胞であることが知られている。今回、物質Aの生産量が2倍以上に増加した「良い」細胞Yを取得したい。どの程度のサンプル数（$${N}$$）を試験すれば、細胞Yの存在を検出できるだろうか？

【回答例】
　細胞Xが生産する物質Aの量は常に一定とは限らない。細胞のロット差、培養環境の些細な違い、観測した時の誤差など、さまざまな要因によってバラツキが常に生じる。指標にもよるが、多くの場合は正規分布に従うとみなして良い。このとき、平均を $${μ_X}$$, 標準偏差を $${σ_X}$$ と置いてみよう。同じように細胞Yに関しても、平均を $${μ_Y}$$, 標準偏差を $${σ_Y}$$ と置いてみる。
　今回の状況では、$${μ_Y = 2 μ_X}$$ である。また、これも指標によるが、一般的には変動係数（$${CV = \frac{σ}{μ}}$$）が一定とみなせる状況が多い。そのため、$${\frac{σ_X}{μ_X} = \frac{σ_Y}{μ_Y}}$$ も成り立つ。以上の状況の下で、細胞Yの性能を検出できるかどうか、を「検出力」の考え方で解決してみたい。

帰無仮説 $${H_0}$$：物質Aの生産量が $${μ_X}$$ である。
対立仮説 $${H_1}$$：物質Aの生産量が $${μ_Y = 2 μ_X}$$ である。
有意水準 $${α}$$：5%（両側検定；試験者が決定する。）
検出力 $${1 - β}$$：80%（試験者が決定する。）
※ サンプル数 $${N}$$, 変動係数 $${CV = \frac{σ_X}{μ_X} = \frac{σ_Y}{μ_Y}}$$

数値は一例であるが、イメージはこの通り。

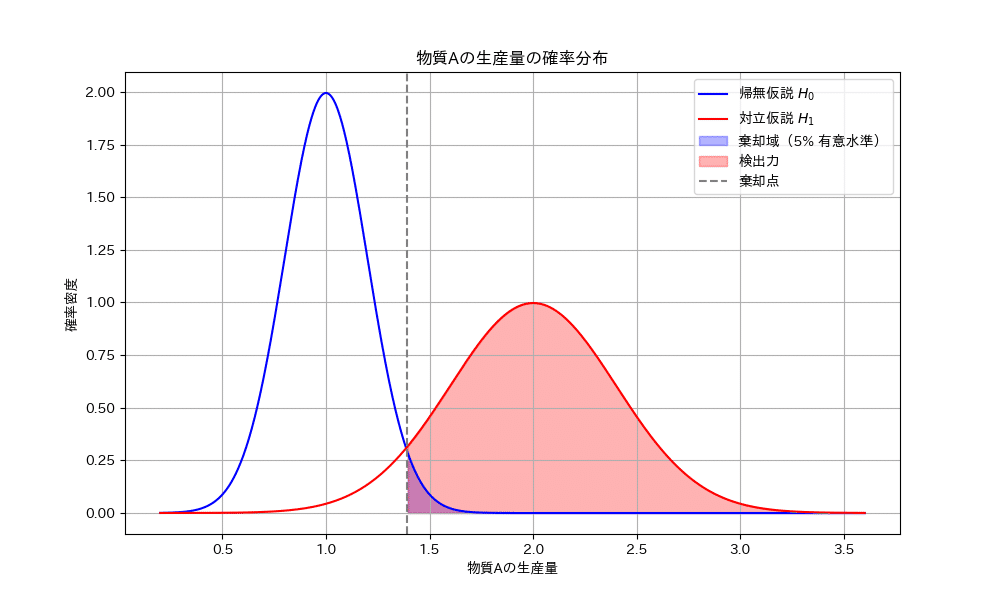
　帰無仮説 $${H_0}$$ が正しいと仮定して、帰無仮説の棄却点 $${\bar{x}}$$ は、 $${\frac{\bar{x} - μ_X}{\frac{σ_X}{\sqrt{N}}} = Z_{0.025} = 1.96}$$ より、$${\bar{x} = (\frac{1.96 CV}{\sqrt{N}} + 1 )  μ_X}$$ である。

　次に対立仮説 $${H_1}$$ が正しいと仮定して、棄却点以上の値を取る確率（＝検出力）は、$${ P(Z ≧ \frac{\bar{x} - μ_Y}{\frac{σ_Y}{\sqrt{N}}})}$$ と書き下すことができ、この値が検出力（0.8）と等しいことが要件である。もう少し数式を整理すると、$${ P(Z ≧ 0.98 - \frac{\sqrt{N}}{2 CV}) = 0.8}$$ を満たせば良い。 

　こうして、変動係数とサンプル数のみを変数とする数式を導出できた。この数式を用いつつ、アッセイ系の変動係数に合わせて必要なサンプル数を決定することが可能になる。

【要点】
　統計解析は非常に心強いが、あくまでツールでしかないことは肝に命じておこう。統計解析は計算方法を教えてくれても、有意水準や検出力をどの程度に設定するか、は自分で決めなければいけない。その意識を持つことで、目の前で起きている現象に寄り添うことができるだろう。

【参考図書】

生命科学・生物工学のための 間違いから学ぶ実践統計解析 | 近代科学社

　この本は手元に持っておきたい良質な一冊である。分子生物学・合成生物学に携わる研究者にとって、痒いところにも手が届く内容となっている。