
"General theory of relativity"(Dirac)を読む6
過去の記事はこちら。
Chapter 6は"Parallel displacement"について。曲がった空間での「平行移動」の話。
そもそも平行移動とは何か?ある2点PとQが与えられた時、この2点間を結ぶ経路を定義することができる。このとき、「2つの平行移動されるベクトルの角は一定に保たれる」+「ベクトルの大きさは変化しない」という2つの要請から「平行移動が」定義される。
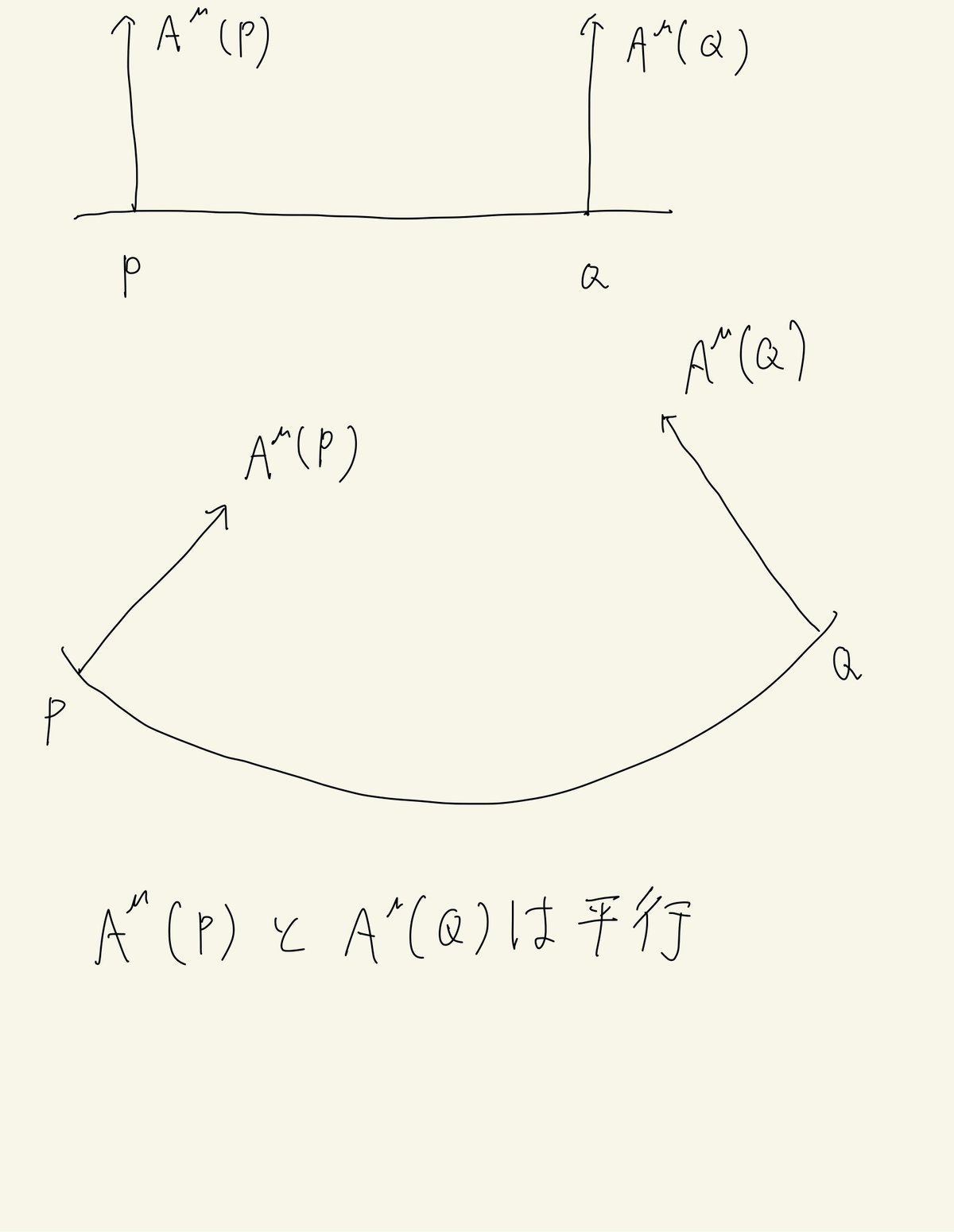
平坦な空間だと、$${A^{\mu}(P)}$$と$${A^{\mu}(Q)}$$が平行なのは理解しやすい(図1上図)。しかし、曲がった空間での平行移動は見た目にはおよそ平行に見えない。しかし、Pから微小距離離れた$${P+\delta P}$$では平行なベクトルを描くことはできる。
また、曲がった空間での平行移動は経路依存性を持つ。

黒矢印のベクトルを2通りの平行移動をさせた結果(赤色と青色の矢印)は異なる。
さて、3次元空間の平坦な空間に住む我々は2次元の曲がった空間をイメージすることができる。例えば、図2の球面上に蟻が存在しているとして、彼らは自分たちが曲面に生活していることを理解できないが、3次元空間に住む我々は、蟻が2次元の曲面に住んでいる事を理解できる。図1や図2で描いた平行移動も、(平坦な)3次元空間に住む我々だからこそ、2次元空間での平行移動を考えることができた。すなわち、同様に、4次元時空での「曲面」も、より高次元の「平らな空間」から考察すれば、平行移動を定義できると考えられる。
ということで、N次元空間での直線座標系$${z^n(n=1,2,…N)}$$を考える。このN次元空間での2点間の微小距離は
$$
d s^2=h_{n m} d z^n d z^m,\tag{6.1}
$$
で与えられる。ただし、$${n,m=1,2,…N}$$であり、テンソルの縮約規則に則り、$${n,m}$$で和を取っている。平坦な高次元時空を考えているので、$${h_{nm}}$$は$${g_{\mu\nu}}$$と異なり、定数である(平坦なミンコフスキー時空での計量も定数であった)。また、計量を用いた添字の上げ下げルールより、$${dz_n=h_{nm}dz^m}$$と表せる。
4次元時空での「曲面」上の点は、より高次の平坦なN次元空間上の点でもあり、4次元時空上で$${x^{\mu}}$$で表される点は、N次元空間上では$${y^{n}(x)}$$と表され、4次元時空$${x^{ \mu}}$$の関数である。
$${y^{n}(x)}$$を$${x^{\mu}}$$で微分すると、
$$
\frac{\partial y^n(x)}{\partial x^\mu}=y_{, \mu}^n
$$
を得る。
4次元時空上の曲面の微小な2点間の距離は、
$$
\delta y^n=y_{, \mu}^n \delta x^\mu\tag{6.2}
$$
で表される。また、これら2点間の(高次元空間上での)距離は、
$$
\delta s^2=h_{n m} \delta y^n \delta y^m=h_{n m} y_{, \mu}^n y_{, \nu}^m \delta x^\mu \delta x^{\nu} .
$$
となり、計量を用いて添字を下げると、$${\delta s^2=y^n_{,\mu} y_{n,\nu} \delta x^\mu \delta x^\nu}$$とも書ける。また、これは$${\delta s^2=g_{\mu\nu}\delta x^{\mu} \delta x^{\nu}}$$とも表せるので、
$$
g_{\mu\nu}=y^n_{,\mu} y_{n,\nu}\tag{6.3}
$$
と書ける。ここで重要な事は、高次元時空での2点間の微小距離が、4次元時空での微小距離に焼き直して議論することができている点で、4次元時空での計量は、高次元時空の点での微分量として表せることである。
ここで、4次元時空のある場所$${x}$$での反変ベクトル$${A^{\mu}}$$を考える。これが十分な微小なベクトルの場合、式(6.2)と同様に、$${A^{\mu}}$$を高次元空間で見ると、
$$
A^n=y^{n},_{\mu}A^{\mu}\tag{6.4}
$$
と書ける。この高次元空間で見た$${A^n}$$を4次元曲面上で微小距離$${x+dx}$$だけ平行移動する。(高次元空間でのベクトルなので、高次元空間上で見ると平行移動させてもベクトルの成分は変わらない。)
しかし、4次元時空の曲面上で見ると、平行移動を行うとベクトルが曲面からはみ出てしまう。そこで、高次元空間で見たベクトルを4次元時空表面に投影すれば、平行移動したベクトルを4次元時空表面上で表すことができる。この時、$${A^n}$$の4次元時空上の曲面に投影した成分を$${A^n_{{\rm tan}}}$$、それに垂直な成分を$${A^n_{{\rm nor}}}$$とすると、
$$
A^{n}=A^n_{{\rm tan}}+A^n_{{\rm nor}}\tag{6.5}
$$
となる。

さて、$${K^{\mu}}$$を$${A^n_{{\rm tan}}}$$の4次元時空の曲面上で対応するベクトルとすると、式(6.4)より、
$$
A_{\text {tan }}^n=K^\mu y_{, \mu}^n(x+d x)\tag{6.6}
$$
となる。(繰り返すが、式(6.4)はあるベクトルを考えたときの4次元時空上で表現と高次元時空上での表現を結びつけるものである)。
定義より、$${A^n_{{\rm nor}}}$$と$${A^n_{{\rm tan}}}$$は垂直なので、任意の$${K^{\mu}}$$に対してその内積は0になる。($${A_{n,{\rm nor}}A^n_{{\rm tan}}=0}$$)。したがって、$${A_{\text {nor }}^n y_{n, \mu}(x+d x)=0}$$である。
さて、式(6.5)に$${y_{n,\nu}(x+dx)}$$を書けると、
$$
A^ny_{n,\nu}(x+dx)=A^n_{{\rm tan}}y_{n,\nu}(x+dx)+A^n_{{\rm nor}}y_{n,\nu}(x+dx)
$$
となるが、右辺第二項は先程の垂直条件の式より0になる。また、式(6.6)を考えると、
$$
\begin{aligned}
A^ny_{n,\nu}(x+dx)&=A^n_{{\rm tan}}y_{n,\nu}(x+dx)\\
&=K^\mu y_{, \mu}^n(x+d x)y_{n,\nu}(x+dx)\\
&=K^{\mu}g_{\mu\nu}(x+dx)
\end{aligned}
$$
最後の等号では式(6.3)を用いた。
計量テンソルを用いて添字を下げると、$${K^{\mu}g_{\mu\nu}(x+dx)=K_{\nu}(x+dx)}$$であることに注意すると
$$
\begin{aligned}
K_\nu(x+d x) &=A^ny_{n,\nu}(x+dx)\\
&=A^n\left[y_{n, \nu}(x)+y_{n, \nu, \sigma} d x^\sigma\right] \\
&=A^\mu y_{, \mu}^n\left[y_{n, \nu}+y_{n, \nu, \sigma} d x^\sigma\right] \\
&=A_\nu+A^\mu y_{, \mu}^n y_{n, \nu, \sigma} d x^\sigma .
\end{aligned}
$$
となる。2番めの等号ではテーラー展開を行い、1次の項だけを残した。3番めの等号では、式(6.4)を代入した。4番目の等号では式(6.3)を用いて、右辺第一項に計量を出現させ、さらに計量を使って添字を下げた。
さて$${K_{\nu}}$$は何だったかというと、4次元時空の曲面上でのベクトル$${A^{\mu}}$$を平坦な高次元時空上で平行移動し、それを4次元時空上に投影したものであった。したがって、
$$
K_{\nu}-A_{\nu}=dA_{\nu}
$$
は$${A^{\mu}}$$を4次元時空の曲面上での平行移動した量であり、
$$
dA_{\nu}=A^\mu y_{, \mu}^n y_{n, \nu, \sigma} d x^\sigma\tag{6.7}
$$
である。以上で、4次元時空の曲面上での平行移動を導出することができた。
(余談)
割と計算が多かったこのChapterでは何をやったかというと、曲面での平行移動を考えるために、より高次元の平坦な時空で平行移動を考え、それを再び4次元時空に投影することによって、4次元時空の曲面での平行移動の導出である。
(よろしかったら、下の「気に入ったらサポート」から応援よろしくおねがいします!)
