TeX ソース:円周角の定理
数学A:図形の性質:平面図形:円周角の定理
Cloud LaTeX に貼り付けるだけの TeX ソースです。私自身が授業で使う教材プリントのために作ったものを、再利用できるように整理してみました。あくまで自分用ですが、良かったら Cloud LaTeX やご自身の TeX ファイルに貼り付けてお使いください。
問題01
\documentclass[dvipdfmx]{jsarticle}
\usepackage{tikz}
\usetikzlibrary{positioning,quotes,angles}
\usepackage{emath}
\begin{document}
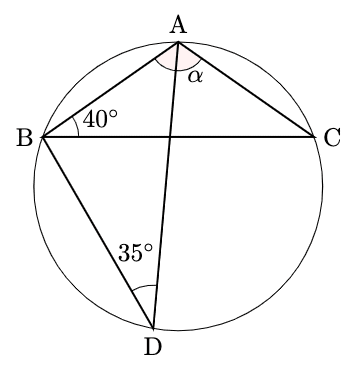
下の図において, $\alpha$を求めよ。
\begin{tikzpicture}[scale=2.0]
\coordinate (O) at (0,0);
\coordinate[label=above:A] (A) at (90:1);
\coordinate[label=left:B] (B) at (160:1);
\coordinate[label=right:C] (C) at (20:1);
\coordinate[label=below:D] (D) at (260:1);
\path pic["$\alpha$",right,draw,fill=red!5!white,angle radius=4mm,angle eccentricity=1.2] {angle = B--A--C};
\path pic["$40\Deg$",draw,angle radius=5mm,angle eccentricity=1.7] {angle = C--B--A};
\path pic["$35\Deg$",draw,angle radius=6mm,angle eccentricity=1.8] {angle = A--D--B};
\draw[thick] (A)--(B)--(C)--cycle;
\draw[thick] (B)--(D)--(A);
\draw (O) circle (1);
\end{tikzpicture}
\end{document}問題02
\documentclass[dvipdfmx]{jsarticle}
\usepackage{tikz}
\usetikzlibrary{positioning,quotes,angles}
\usepackage{emath}
\begin{document}
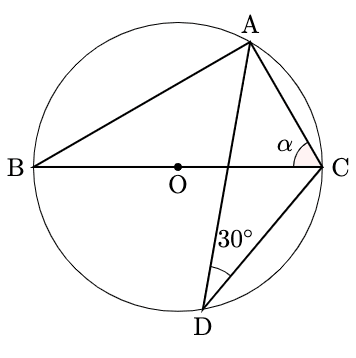
下の図において, $\alpha$を求めよ。ただし, Oは円の中心, 線分BCは円の直径である。
\begin{tikzpicture}[scale=2.0]
\coordinate[label=below:O] (O) at (0,0);
\coordinate[label=above:A] (A) at (60:1);
\coordinate[label=left:B] (B) at (180:1);
\coordinate[label=right:C] (C) at (0:1);
\coordinate[label=below:D] (D) at (280:1);
\path pic["$\alpha$",draw,fill=red!5!white,angle radius=4mm,angle eccentricity=1.5] {angle = A--C--B};
\path pic["$30\Deg$",draw,angle radius=6mm,angle eccentricity=1.8] {angle = C--D--A};
\draw[thick] (A)--(B)--(C)--cycle;
\draw[thick] (C)--(D)--(A);
\draw (O) circle (1);
\fill (O) circle (.8pt);
\end{tikzpicture}
\end{document}問題03
\documentclass[dvipdfmx]{jsarticle}
\usepackage{tikz}
\usetikzlibrary{positioning,quotes,angles}
\usepackage{emath}
\begin{document}
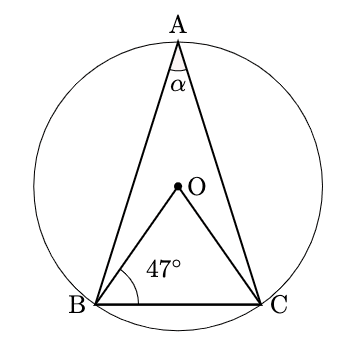
下の図において, $\alpha$を求めよ。ただし, Oは円の中心である。
\begin{tikzpicture}[scale=2.0]
\coordinate[label=right:O] (O) at (0,0);
\coordinate[label=above:A] (A) at (90:1);
\coordinate[label=left:B] (B) at (235:1);
\coordinate[label=right:C] (C) at (305:1);
\path pic["$\alpha$",draw,fill=red!5!white,angle radius=4mm,angle eccentricity=1.5] {angle = B--A--C};
\path pic["$47\Deg$",draw,angle radius=6mm,angle eccentricity=1.8] {angle = C--B--O};
\draw[thick] (A)--(B)--(C)--cycle;
\draw[thick] (O)--(B)--(C)--cycle;
\draw (O) circle (1);
\fill (O) circle (.8pt);
\end{tikzpicture}
\end{document}問題04
\documentclass[dvipdfmx]{jsarticle}
\usepackage{tikz}
\usetikzlibrary{positioning,quotes,angles,intersections}
\usepackage{emath}
\begin{document}
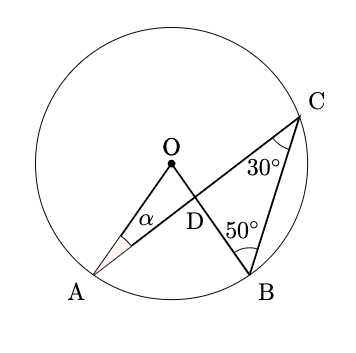
% 下の図において, $\alpha$を求めよ。ただし, Oは円の中心とする。
\begin{tikzpicture}[scale=2.0]
%点の定義
\coordinate[label=above:O] (O) at (0,0);
\coordinate[label=below left:A] (A) at (235:1);
\coordinate[label=below right:B] (B) at (305:1);
\coordinate[label=above right:C] (C) at (20:1);
\path[name path=AC] (A)--(C);
\path[name path=OB] (O)--(B);
\path[name intersections = {of = OB and AC,by = {D}}];
%図形描画
\draw (O) circle (1);
\fill (O) circle (.8pt) node[above] {O};
\fill (D) circle (0) node[below=3pt] {D};
\draw[thick] (A)--(O)--(B);
\draw[thick] (A)--(C)--(B);
\path pic["$\alpha$",draw,fill=red!5!white,angle radius=7mm,angle eccentricity=1.6] {angle = C--A--O};
\path pic["$50\Deg$",draw,angle radius=4mm,angle eccentricity=1.7] {angle = C--B--O};
\path pic["$30\Deg$",draw,angle radius=5mm,angle eccentricity=1.8] {angle = A--C--B};
\end{tikzpicture}
\end{document}問題05
\documentclass[dvipdfmx]{jsarticle}
\usepackage{tikz}
\usetikzlibrary{positioning,quotes,angles}
\usepackage{emath}
\begin{document}
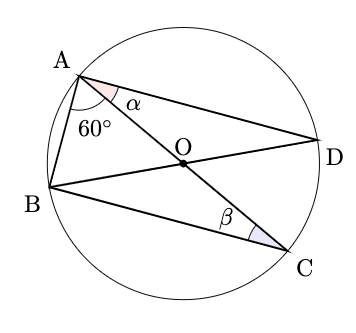
% 下の図において, $\alpha$, $\beta$を求めよ。ただし, Oは円の中心とする。
\begin{tikzpicture}[scale=2.0]
%点の定義
\coordinate[label=above:O] (O) at (0,0);
\coordinate[label=above left:A] (A) at (140:1);
\coordinate[label=below left:B] (B) at (190:1);
\coordinate[label=below right:C] (C) at (320:1);
\coordinate[label=below right:D] (D) at (10:1);
%図形描画
\draw (O) circle (1);
\fill (O) circle (.8pt);
\path pic["$\alpha$",draw,fill=red!10!white,angle radius=6mm,angle eccentricity=1.5] {angle = C--A--D};
\path pic["$\beta$",draw,fill=blue!10!white,angle radius=6mm,angle eccentricity=1.7] {angle = A--C--B};
\path pic["$60\Deg$",draw,angle radius=5mm,angle eccentricity=1.6] {angle = B--A--O};
\draw[thick] (A)--(B)--(D)--(A)--(C)--(B)--cycle;
\end{tikzpicture}
\end{document}問題06
\documentclass[dvipdfmx]{jsarticle}
\usepackage{tikz}
\usetikzlibrary{positioning,quotes,angles}
\usepackage{emath}
\begin{document}
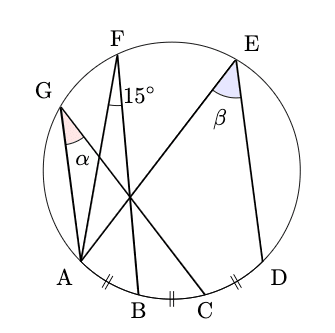
% 下の図において, $\alpha$, $\beta$を求めよ。
\begin{tikzpicture}[scale=2.0]
%点の定義
\coordinate (O) at (0,0);
\coordinate[label=below left:A] (A) at (225:1);
\coordinate[label=below:B] (B) at (255:1);
\coordinate[label=below:C] (C) at (285:1);
\coordinate[label=below right:D] (D) at (315:1);
\coordinate[label=above right:E] (E) at (60:1);
\coordinate[label=above:F] (F) at (115:1);
\coordinate[label=above left:G] (G) at (150:1);
%図形描画
\draw (O) circle (1);
\path pic["$\alpha$",draw,fill=red!10!white,angle radius=6mm,angle eccentricity=1.5] {angle = A--G--C};
\path pic["$\beta$",draw,fill=blue!10!white,angle radius=6mm,angle eccentricity=1.6] {angle = A--E--D};
\path pic["$15\Deg$",draw,angle radius=8mm,angle eccentricity=1.1,above right] {angle = A--F--B};
\draw[thick,rounded corners=1pt] (A)--(G)--(C);
\draw[thick,rounded corners=1pt] (A)--(F)--(B);
\draw[thick,rounded corners=1pt] (A)--(E)--(D);
\draw ([shift={(0,0)}]225:1) arc[radius=1, start angle=225, end angle= 255] node[midway,sloped] {\scriptsize $\|$};
\draw ([shift={(0,0)}]255:1) arc[radius=1, start angle=255, end angle= 285] node[midway,sloped] {\scriptsize $\|$};
\draw ([shift={(0,0)}]285:1) arc[radius=1, start angle=285, end angle= 315] node[midway,sloped] {\scriptsize $\|$};
\end{tikzpicture}
\end{document}更新履歴
2021.01.16...問題01, 02, 03, 04, 05, 06を新規登録
