線形ではない関係性をモデル化する方法。そもそもモデルってなに?
データの関係性をモデル化するとき、「線形モデルではうまくフィットしない…」 ということはありませんか?多次元の線形モデルでは逆にオーバーフィットしてうまくいかないこともあります。
特に、呼吸器増悪回数と肺機能低下(FEV1)の関係のように、直線では表現しにくいパターン では、より柔軟なアプローチが必要です。
そこで活躍するのが 「一般化加法モデル(Generalized additive model)」。GAMを使えば、平滑スプライン(Smoothing Splines)を適用し、データのトレンドを適切に捉えつつオーバーフィットを防ぐ ことができます。
本記事では、モデル の基本から R(mgcv パッケージ)での一般化加法モデルの実装方法まで解説 します!
1. 今回の論文:喫煙歴がある肺機能正常集団の、急性増悪とその後の肺機能低下との関連を示した研究
Respiratory Exacerbations and Lung Function Decline in People with Smoking History and Normal Spirometry(AJRCCM in press)
🔍 研究の目的
本研究では、喫煙歴があるがスパイロメトリーが正常な人々において、呼吸器増悪が肺機能低下やCOPD進行、死亡率とどのように関連しているかを評価することを目的としています。
つまりCOPDの診断基準を満たしてない人でも、COPD増悪みたいな症状を起こす人っているよね。
その人たちがその「COPD増悪もどき」後にどれくらい肺機能が低下し、実際COPDになる人がどれくらいいて、死亡率にどれくらい影響を与えるのかというリサーチクエスチョンです。
👥 研究デザイン
デザイン: COPDGene Study(米国の多施設前向きコホート)を用いた前向きコホート
対象者: 10,194人の喫煙者のうち、3,210人の正常スパイロメトリーの参加者を対象
暴露:
ベースライン(visit 1)から5年後(visit 2)の間の呼吸器増悪回数
呼吸器増悪は、抗菌薬あるいはステロイドを使用した呼吸器症状の悪化と定義
評価項目:
肺機能(FEV1)低下率
COPDへの進行率
全死亡率
📊 主要な結果
① 呼吸器増悪と肺機能低下
1回の増悪ごとにFEV1が年間2.96 ml低下(95% CI: 1.81-4.12, P<0.001)
重症増悪(ER受診・入院)のある患者はFEV1の低下が14.6 ml/年とより顕著(95% CI: 8.56-20.6, P<0.001)
② COPDへの進行リスク
呼吸器増悪が多いほどCOPDへ進行するリスクが上昇
1回の増悪ごとにCOPD発症リスクが6%増加(OR = 1.06, 95% CI: 1.006-1.11, P=0.022)
③ 呼吸器増悪と死亡率
重症増悪を経験した群の死亡率は17.1%で、増悪のない群(9.8%)と比較して有意に高い(HR = 1.97, 95% CI: 1.40-2.77, P<0.001)
2. 統計解析:加法モデル(Additive Model)とは?
本研究では、呼吸器増悪と肺機能低下の関係を解析するために、加法モデル(Additive Model) が用いられました。加法モデルってなんなのか、0から説明します。
こちらを参考にしました。
a. そもそもモデルって?―パラメトリックとノンパラメトリック
臨床研究において我々がやりたいことは、予測なんです。
つまり、介入(例:治療A)がある場合とない場合でのアウトカム(例:肺機能)を予測し、それらを比較します。
例①:治療Aを行った場合と行わなかった場合の、その後の肺機能の変化をみています。この場合は単純です。ここにあるデータだけを使って、それぞれの群(A=0 or 1)の肺機能の変化の平均値を計算し、比較すればいいのです。
このデータのみによって推定値をもとめる手法をノンパラメトリックと呼んでいます。

肺機能のベースラインからの変化(mL)
例②:では次の場合はどうでしょう。治療Aの投与量(X軸、mg)が変化した場合、肺機能のベースラインからの変化(Y軸、mL)はどうかわるかをみています。つまり知りたいのは、治療Aの投与量を増やしたとき(例:50 mgから90 mg)に、肺機能がどれくらい増加するかです。
しかし、治療A 50 mg、90 mgの部分にちょうどいいドットがないので、肺機能の変化をデータから直接計算することができません。これでは先ほどのようなノンパラメトリックな手法は使えません。

ここでデータに対してモデルを当てはめて回帰分析を行う必要がでてきます。下の図はドットに線形モデルを当てはめています。

これにより、
Y(肺機能の変化量)= β0 + β1×X(Aの投与量)
と線形モデルに当てはめることができます。こうすると、投与量が増えたときの肺機能の変化量を、傾き(β1)を用いて計算することが可能です。
このように、データに加えて、推定値の値に対する事前の制約(モデルなど)を利用する方法をパラメトリック手法と呼びます。その最も単純な例が線形モデルです。
ただデータセットが複雑であればあるほど、単純な線形モデル(一直線の線)での推定が困難になってきます。つまり直線から外れたドットが多くなる場合がありますよね。そのような時により複雑なモデルを使う必要がでてきます。
b. 高次元の線形モデルとその弱点
線形モデルって、実は直線だけではないんです。
線形モデルの定義は、目的変数(予測したい値)が、説明変数に一定の係数を掛けて足し合わせた形で表される統計モデルのことです。説明変数に2乗や対数を含んでも、係数が直線的に関与していれば線形モデルとみなされます。

このような高次元の線形モデルを用いることで、より複雑な関係性もモデルに当てはめることが可能です。しかも解釈がシンプル(2次関数ならU字型、3次関数ならS字型など)です。
ただし、次数を増やすとオーバーフィットしやすかったり、より複雑な非線形関係はフィットしにくかったりします。そのような場合に、より柔軟な加法モデルの出番です!
c. 加法モデルと線形モデルの違い・関係性
加法モデルとは、平滑スプラインを用いて、非線形の滑らかな関数を適用できるモデル
加法モデル(Additive model)は、線形モデルを拡張して、各説明変数ごとにスムーズ関数(Smooth function)を適用できるモデルです。通常スムーズ関数として、平滑スプラインを用います。

のように、説明変数ごと(x1, x2)に非線形な関係をとることが可能ですが、それぞれの効果は足し算で表される点は、線形モデルと共通しています。
加法モデルは、目的変数が正規分布に従う場合を想定していますが、一般化加法モデルは、目的変数が正規分布以外の確率分布を持つ場合にも対応できます。
d. 平滑スプラインの仕組み
平滑スプラインは、データの変動をなめらかに補間する方法で、スプライン関数を自由に曲げながら最適なフィットを見つける手法です。過学習を防ぐためにデータのドットを全て通ろうとせず、適度に滑らかに補間します。つまりモデルの複雑さと誤差を考慮して、最適な曲線の滑らかさを自動的に決めてくれる手法です。
平滑スプラインでは、一般化交差検証(Generalized Cross-Validation)という方法を使って、自動で補間してくれます。スムージングパラメタ(λ)を調整し、もっともフィットが良い曲線を自動で選択してくれる仕組みです。

e. 加法モデルを実際にデータに当てはめてみる
Rの加法モデルのパッケージ "mgcv" に「オートバイ事故の衝撃データ」というサンプルデータセットが含まれていたので、実際に試してみましょう。
library(MASS)
library(ggplot2)
data("mcycle")
ggplot(mcycle, aes(x = times, y = accel)) +
geom_point(alpha = 0.5) +
labs(title = "時間と加速度の関係",
x = "時間 (ms)",
y = "加速度 (g)") +
theme_minimal()
これはオートバイの衝突直後からの時間と、加速度の関係を示しています。これはどうみても線形モデルに当てはめるのは難しそうです。
ggplot(mcycle, aes(x = times, y = accel)) +
geom_point(alpha = 0.5) +
geom_smooth(method = "lm", color = "blue", se = TRUE) +
labs(title = "時間と加速度の関係",
x = "時間 (ms)",
y = "加速度 (g)") +
theme_minimal()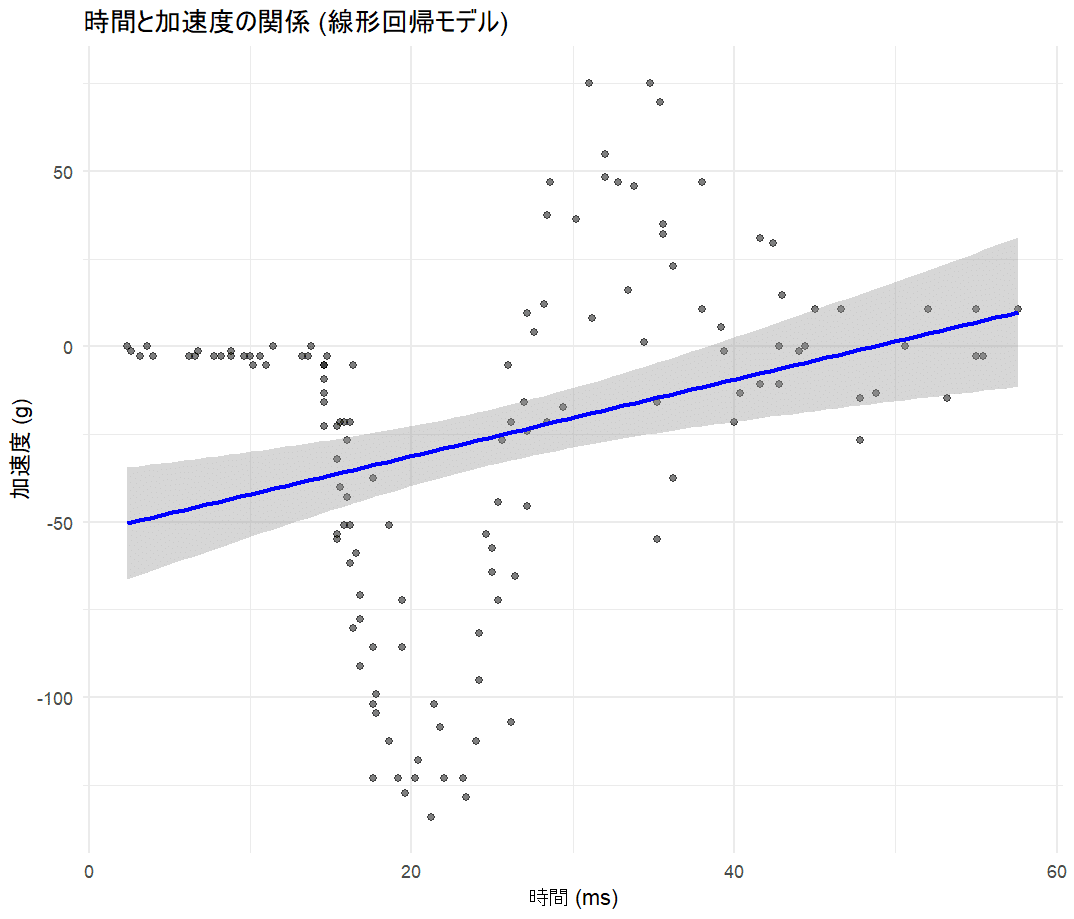
線形モデルはやはり厳しそうです。
そこで今回は加法モデルを使用してみましょう!
Rの"mgcv"パッケージを用いて、加法モデルを使用することができます。"accel"が目的変数の加速度、"times"が説明変数の衝突からの時間です。s()がスムーズ関数に当てはめていることを表します。bs="cs"でスムーズ関数として平滑スプラインを使用することを指定しています。
library(mgcv)
#線形回帰
lm.model <- lm(accel ~ times, data=mcycle)
#加法モデル
gam.model <- gam(accel ~ s(times, bs="cs"), data=mcycle) 実際の観測データに関数を当てはめてみます。
library(ggplot2)
ggplot(mcycle, aes(x = times, y = accel)) +
geom_point(alpha = 0.5) +
geom_smooth(method = "gam", formula = y ~ s(x, bs = "cs"), color = "blue", fill = "lightblue", se = TRUE) +
labs(title = "時間と加速度の関係 (平滑スプライン)",
x = "時間 (ms)",
y = "加速度 (g)") +
theme_minimal()
うまいこと滑らかに関数がフィットしているようです。
このようにオーバーフィットを防ぎながら非線形の関係をモデル化する場合、平滑化スプラインは非常に便利です。
3. まとめ
一般化加法モデルは、説明変数に平滑スプライン関数を適用することで、より柔軟なモデリングが可能になる
平滑スプライン関数は、スプライン関数を基にオーバーフィットを避けるためより滑らかな関数に自動で補間してくれる
Rでは、mgcvパッケージを用いて実装が可能
次回もお楽しみに!
2025/2/21
いいなと思ったら応援しよう!