コレスポンデンス分析の同時布置図は本当に使えないのか?
この記事は以下のはてなブログからの転載です。
はじめに
松本健太郎さんの「マーケティングリサーチで使われるコレスポンデンス分析について調べてみた」という記事が書かれたころからでしょうか、コレスポンデンス分析(以下、コレポン)の同時布置図に対する否定的な意見をよく目にするようになりました。
松本さんの議論は
どの年代で見ても20代の購入量は圧倒的なのです。そのような見方は、数量で見れば違和感を覚えます。
という疑問をきっかけに
コレスポンデンス分析は、それぞれ行得点・列得点を算出しているだけで、それらを重ね合わせたに過ぎません。 つまり列要素と行要素との距離は、数理的に定義されず「近い」「似ている」のように解釈できないのです。
というところから
コレスポンデンス分析は行・列をごっちゃにして分析しない。
という結論に至っています。
この記事に対する反響も大きく、Twitterでも同調する意見に多くの「いいね」が付いています。
マーケティングリサーチで使われるコレスポンデンス分析について調べてみた|松本健太郎 @matsuken0716|note(ノート) https://t.co/PnHq6hSYC5
— 松本健太郎 (@matsuken0716) June 10, 2019
ポジショニングで盛り上がっているので便乗しますが、「イメージ項目」と「ブランド」を同時にプロットした「コレスポンデンス分析」とやらを、調査会社の皆さんには早く根絶していただけると、僕の仕事のひと手間が省けて嬉しいですw
— 高橋孝之|ホジョセン (@inyuinyu) January 24, 2021
松本さんが完結にまとめてくれてます。https://t.co/W1QHqe0KUB
私は統計の専門性低いので細部の理解は怪しいですが、弊社内では「コレポンはそれっぽく理解した気になるだけでミスリードもあり使えない」という扱いになってますね。
— 山口義宏 𝑰𝒏𝒔𝒊𝒈𝒉𝒕𝒇𝒐𝒓𝒄𝒆 (@blogucci) January 3, 2022
マーケティングリサーチで使われるコレスポンデンス分析について調べてみた|松本健太郎 @matsuken0716 https://t.co/7j6IHiMEw7
松本さんの問題提起より前からコレポンの同時布置図の解釈について否定的な意見は散見されました。 例えば朝野先生による解説でも
行要素と列要素を別々の散布図に書くというグラフィック表現が手堅い対応でしょう。
と結論付けらえています。
確かにコレポンの誤った解釈は時折目にしますし、調査会社のサイトにある手法説明にも誤ったものを見かけます。
本当にコレポンの同時布置図は使ってはいけないようなものなのでしょうか?
しかし、実務で何十枚もコレポンの同時布置図を描いてきた者としては疑問符が浮かびます。
「それって、同時布置図の正しい解釈を知らないだけじゃないの???」
結論
先に私の結論を書きます。
* コレポンの同時布置図において集計表の行と列の関係は角度の大きさで解釈できるよ
* コレポンの同時布置図が表現しようとしているのは割合の残差であり、残 差の大きさは原点から引いた各点がなす角度の大きさとして表現されるよ。
* コレポンは実数の大きさには関心がないよ。
* 残差の大きさが角度の大きさとして表される描画方法を使わないとダメだよ。
* 原点から各点へ矢印を引くと解釈しやすいよ。
* 縦横のスケールは合わせないとダメだよ。
* 縦横の軸の意味を解釈しようとするのはダメだよ。
* 点と点の距離で関係の強さを解釈しようとするのはダメだよ。
解説
ここからはRのコードを交えて説明を進めます。
サンプルデータ
松本さんと同じデータを使うのが本当ならいいんでしょうが、松本さんのデータには馬蹄形問題が潜んでいて、話が若干ややこしくなります。
なので、今回はコレポンの話に絞るためにこちらのデータを使います。 これは架空のブランドのブランドイメージ調査のデータになっています。
サンプルデータを用意します。
(dat <- c(5, 18, 19, 12, 3, 7, 46, 29, 40, 7, 2, 20, 39, 49, 16) |>
matrix(
nrow = 5,
dimnames = list(
Brands = c("Butterbeer", "Squishee", "Slurm", "Fizzy Lifting Drink", "Brawndo"),
Attributes = c("Tasty", "Aesthetic", "Economic")
)
))
## Attributes
## Brands Tasty Aesthetic Economic
## Butterbeer 5 7 2
## Squishee 18 46 20
## Slurm 19 29 39
## Fizzy Lifting Drink 12 40 49
## Brawndo 3 7 16コレポンの実行
まずはとにかくコレポンを実行してみましょう。
Rでコレポンを実行するパッケージは複数ありますが、今回はデータの取り出しやすさからcaパッケージのca()関数を使用します。
library(ca)
res.ca_ca <- ca(dat)
summary(res.ca_ca)
##
## Principal inertias (eigenvalues):
##
## dim value % cum% scree plot
## 1 0.070369 84.5 84.5 *********************
## 2 0.012892 15.5 100.0 ****
## -------- -----
## Total: 0.083260 100.0
##
##
## Rows:
## name mass qlt inr k=1 cor ctr k=2 cor ctr
## 1 | Bttr | 45 1000 190 | -549 854 192 | -227 146 180 |
## 2 | Sqsh | 269 1000 378 | -333 948 425 | 78 52 126 |
## 3 | Slrm | 279 1000 92 | 81 237 26 | -145 763 452 |
## 4 | FzLD | 324 1000 153 | 173 759 138 | 97 241 239 |
## 5 | Brwn | 83 1000 186 | 431 997 220 | -24 3 4 |
##
## Columns:
## name mass qlt inr k=1 cor ctr k=2 cor ctr
## 1 | Tsty | 183 1000 242 | -254 585 168 | -214 415 649 |
## 2 | Asth | 413 1000 256 | -202 790 239 | 104 210 348 |
## 3 | Ecnm | 404 1000 502 | 321 999 593 | -10 1 3 |そして、同時布置図を描きます。
いろいろオプションが付いたり、見慣れない矢印があったりしますがいったんこのまま進めます。
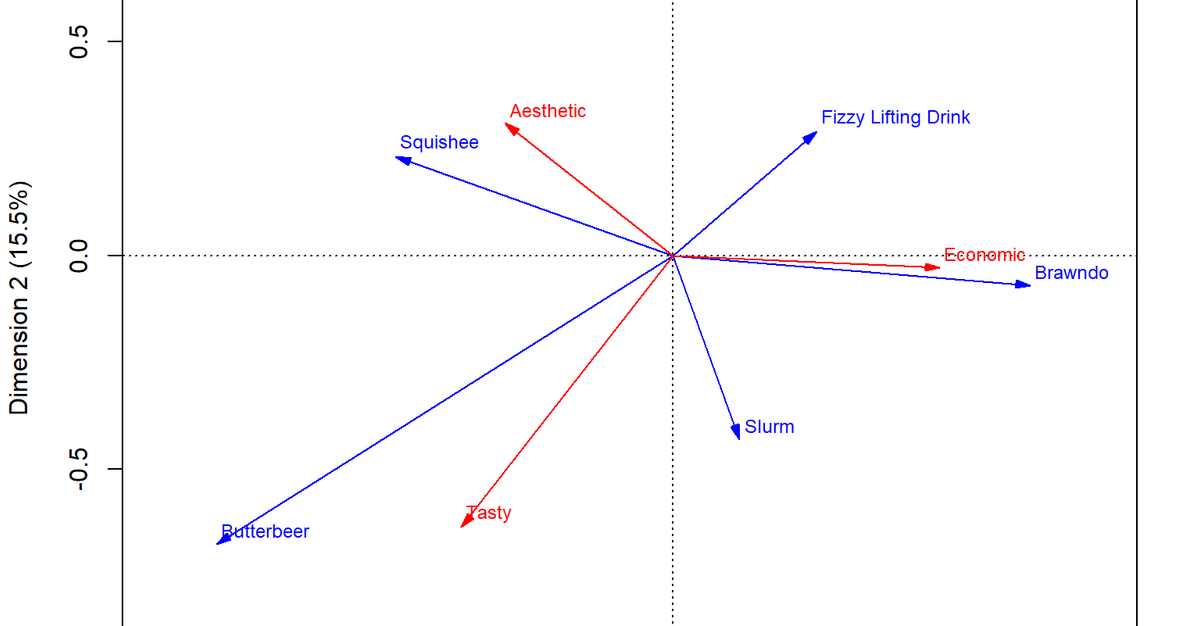
res.biplot_symbiplot <- plot(res.ca_ca,
map = "symbiplot",
arrows = c(TRUE, TRUE),
xlim = c(-1.1, 0.9),
ylim = c(-1.1, 0.9),
main = "ca - Biplot - symbiplot")
各点の座標は以下のようになっています。
res.biplot_symbiplot
## $rows
## Dim1 Dim2
## Butterbeer -1.0665778 -0.67407378
## Squishee -0.6468361 0.23054640
## Slurm 0.1563567 -0.42910993
## Fizzy Lifting Drink 0.3359331 0.28929206
## Brawndo 0.8359247 -0.06979996
##
## $cols
## Dim1 Dim2
## Tasty -0.4937814 -0.63528783
## Aesthetic -0.3915076 0.30897357
## Economic 0.6242065 -0.02893797
ちなみにfactoextraパッケージのfviz_ca()を使うとggplot2ベースの同時布置図も描けます。
library(factoextra)
fviz_ca(res.ca_ca,
map = "symbiplot",
arrows = c(TRUE, TRUE),
title = "CA - Biplot - symbiplot") +
scale_x_continuous(limits = c(-1.1, 0.9)) +
scale_y_continuous(limits = c(-1.1, 0.9))
指標化残差
さて、先に「コレポンの同時布置図が表現しようとしているのは割合の残差」と書きました。
ここでいう残差(residual)とは「実測値と期待値の差」を意味します。
クロス集計表における残差分析の残差と同じです。
今回のデータの残差を計算してみましょう。
総度数nを算出
(n <- sum(dat))
## [1] 312観測割合P(observed proportions、各セルの度数を総度数で割った値、同時確率分布)を算出
(P <- dat / n)
## Attributes
## Brands Tasty Aesthetic Economic
## Butterbeer 0.016025641 0.02243590 0.006410256
## Squishee 0.057692308 0.14743590 0.064102564
## Slurm 0.060897436 0.09294872 0.125000000
## Fizzy Lifting Drink 0.038461538 0.12820513 0.157051282
## Brawndo 0.009615385 0.02243590 0.051282051
行質量(row masses, 行周辺確率分布)と列質量(column masses, 行周辺確率分布)を算出
(row_masses_pi <- rowSums(P))
## Butterbeer Squishee Slurm Fizzy Lifting Drink
## 0.04487179 0.26923077 0.27884615 0.32371795
## Brawndo
## 0.08333333
(col_masses_pj <- colSums(P))
## Tasty Aesthetic Economic
## 0.1826923 0.4134615 0.4038462
期待割合E(Expected proportions)を算出
(E <- row_masses_pi %o% col_masses_pj)
## Tasty Aesthetic Economic
## Butterbeer 0.008197732 0.01855276 0.01812130
## Squishee 0.049186391 0.11131657 0.10872781
## Slurm 0.050943047 0.11529216 0.11261095
## Fizzy Lifting Drink 0.059140779 0.13384492 0.13073225
## Brawndo 0.015224359 0.03445513 0.03365385
残差R(Residuals)を算出
(R <- P - E)
## Attributes
## Brands Tasty Aesthetic Economic
## Butterbeer 0.007827909 0.003883136 -0.01171105
## Squishee 0.008505917 0.036119329 -0.04462525
## Slurm 0.009954389 -0.022343442 0.01238905
## Fizzy Lifting Drink -0.020679241 -0.005639793 0.02631903
## Brawndo -0.005608974 -0.012019231 0.01762821
残差は集計表の行と列のカテゴリ間に関係がないという仮定のもとで期待される値(E、期待値、期待割合)と実際に観測された値(P、観測値、観測割合)の差です。
残差の絶対値が大きいと期待値とズレている、すなわち行と列のカテゴリ間に何らかの関係がありそう、ということになります。
クロス集計表の残差分析と基本的な考え方は同じですが、クロス集計表の残差分析が生の度数の残差を分析するのに対して、コレスポンデンス分析が分析するのは割合の残差であるところが異なります。
生の残差は各カテゴリの度数に左右されるため、期待値で割って正規化します。
これを指標化残差I(Indexed residuals)と呼びます。
(I <- R / E)
## Attributes
## Brands Tasty Aesthetic Economic
## Butterbeer 0.9548872 0.20930233 -0.6462585
## Squishee 0.1729323 0.32447398 -0.4104308
## Slurm 0.1954023 -0.19379845 0.1100164
## Fizzy Lifting Drink -0.3496613 -0.04213677 0.2013201
## Brawndo -0.3684211 -0.34883721 0.5238095
指標化残差が0.955であれば、観測値は期待値より95.5pt高いということを意味します。
P/E
## Attributes
## Brands Tasty Aesthetic Economic
## Butterbeer 1.9548872 1.2093023 0.3537415
## Squishee 1.1729323 1.3244740 0.5895692
## Slurm 1.1954023 0.8062016 1.1100164
## Fizzy Lifting Drink 0.6503387 0.9578632 1.2013201
## Brawndo 0.6315789 0.6511628 1.5238095
この指標化残差を可視化するのがコレポンの同時布置図のねらいです。
コレポンにおける指標化残差の表現
コレポンの同時布置図において、行の点Aの座標を(x1, y1)、列の点Bの座標を(x2, y2)とすると、x1 * x2 + y1 * y2が指標化残差と一致します。
これは二つのベクトルの内積(スカラー積)を意味します。
例えばtastyとButterbeerの指標化残差は0.955。
先に描いたコレポンの同時布置図でのそれぞれの座標は、tastyが(-0.494, -0.635)、Butterbeerが(-1.067, -0.674)。
上記の計算をすると0.955で指標化残差と一致します。
res.biplot_symbiplot$rows[1, 1] *
res.biplot_symbiplot$cols[1, 1] +
res.biplot_symbiplot$rows[1, 2] *
res.biplot_symbiplot$cols[1, 2]
## [1] 0.9548872つまり、コレポンの同時布置図上でtastyとButterbeerの内積が指標化残差を表現できていることが分かります。
内積によって、2つのベクトルがなす角度も定まるので、 バイプロット上でtastyとButterbeerのベクトルがなす角度が標準化残差を表している。といえます。
次に、原点からの距離に注目します。
(dist_Butterbeer <- sqrt((0 - res.biplot_symbiplot$rows[1, 1])^2 + (0 - res.biplot_symbiplot$rows[1, 2])^2))
## [1] 1.26173(dist_Tasty <- sqrt((0 - res.biplot_symbiplot$cols[1, 1])^2 + (0 - res.biplot_symbiplot$cols[1, 2])^2))
## [1] 0.8046184今度は2つのベクトルの角度を算出します。
library(Morpho)
Butterbeer <- as.matrix(c(res.biplot_symbiplot$rows[1, 1], res.biplot_symbiplot$rows[1, 2]))
Tasty <- as.matrix(c(res.biplot_symbiplot$cols[1, 1], res.biplot_symbiplot$cols[1, 2]))
(Butterbeer_Tasty_angle <- angle.calc(Butterbeer, Tasty) / pi * 180)
## [1] 19.85088ここでAのベクトルの長さ*Bのベクトルの長さ*cos(AとBのなす角度)が指標化残差と一致します。
dist_Butterbeer *
dist_Tasty *
cos(Butterbeer_Tasty_angle * pi / 180)
## [1] 0.9548872やはり、2つのベクトルがなす角度が、行と列の2つのカテゴリの指標化残差を表せています。
注目したいのはこの式の最初の2つの部分が、ベクトルの長さになっていることです。
つまり、原点からの距離が遠い点ほど、その点ともう一方の点との関連が強くなることを表しています。
注意!
ここまでで、コレポンの同時布置図が行と列のカテゴリ間の関連を適切に表現できていることに納得いただけたかと思います。
ただし、ここでいくつか注意すべき点があります。
同時布置図を描く方法によって、これらの法則が保たれない場合があるのです。
caパッケージのplot.ca()やfactoextraのfviz_ca()のmapオプションで方法を指定できますが、指標化残差を角度やベクトルの長さで表現できるのは"colprincipal"、"rowprincipal"、"symbiplot"の三つです。
デフォルトの"symmetric"や他の方法ではこの法則が保たれません。
まとめ
コレポンの同時布置図は、2つのグループ(今回のサンプルデータではブランドと属性)の間およびグループ内の相対的な関係を分析するために使用されます。
コレポンは、相対的な関係しか表しません。
実数の大きさは元の集計表で確認しましょう。コレポンでは表現されません。
原点から離れれば離れるほど、より特徴的になります。原点に近いほど偏りがないことになります。
縦横のスケールを合わせること。そうしないと見かけ上の角度が歪んでしまいます。
さいごに
ここで、再び松本さんの記事へ立ち戻りましょう。
どの年代で見ても20代の購入量は圧倒的なのです。そのような見方は、数量で見れば違和感を覚えます。
それはコレポンが相対的な関係を表すもので、実数を表すものではないからです。
コレスポンデンス分析は、それぞれ行得点・列得点を算出しているだけで、それらを重ね合わせたに過ぎません。 つまり列要素と行要素との距離は、数理的に定義されず「近い」「似ている」のように解釈できないのです。
行と列の点の距離で関係を論じられないのはその通りですが、ベクトルの角度と長さによって指標化残差としてそれは表現されています。
コレスポンデンス分析は行・列をごっちゃにして分析しない。
これはさすがに「羹に懲りて膾を吹く」というものです。
コレポンの同時布置図は正しく描いて、正しく解釈すればクロス集計表を解釈する上での強力な道具になりえます。
松本さんのデータをこれまで説明したやり方で同時布置図にするとこうなります。
drink <- c(
1025, 270, 331, 270, 81, 6233, 1618, 1155, 667, 180, 1318, 389, 309, 229, 70,
1209, 219, 239, 349, 200, 5167, 769, 797, 1121, 646
) |>
matrix(
nrow = 5,
byrow = TRUE,
dimnames = list(
銘柄 = c("生茶", "伊右衛門", "綾鷹", "十六茶", "お~いお茶"),
年代 = c("20代", "30代", "40代", "50代", "60代")
)
)
drink |>
ca() |>
fviz_ca(
map = "symbiplot",
arrows = c(TRUE, TRUE),
title = "Drink") +
scale_x_continuous(limits = c(-1.5, 0.75)) +
scale_y_continuous(limits = c(-1.25, 1))
ここから解釈できるのは、
* 20代は原点に近くブランドの選好に相対的な特徴は見られない。全体におけるブランドの割合と大きな差がない。
* 40代は「生茶」が全体と比べて相対的に多く選ばれている。
*60代は「お~いお茶」や「十六茶」が全体と比べて相対的に多く選ばれている。
といったところでしょうか。
繰り返しになりますが、コレポンは実数には関心がないので、そこはモザイクプロットなどで観察しましょう。
そもそも、20代が6割を占めているデータなので、20代が「全体におけるブランドの割合と大きな差がない」のも当然ですね。
library(vcd)
drink |>
t() |>
mosaic(shade=TRUE, legend=TRUE, main="drink", direction="v")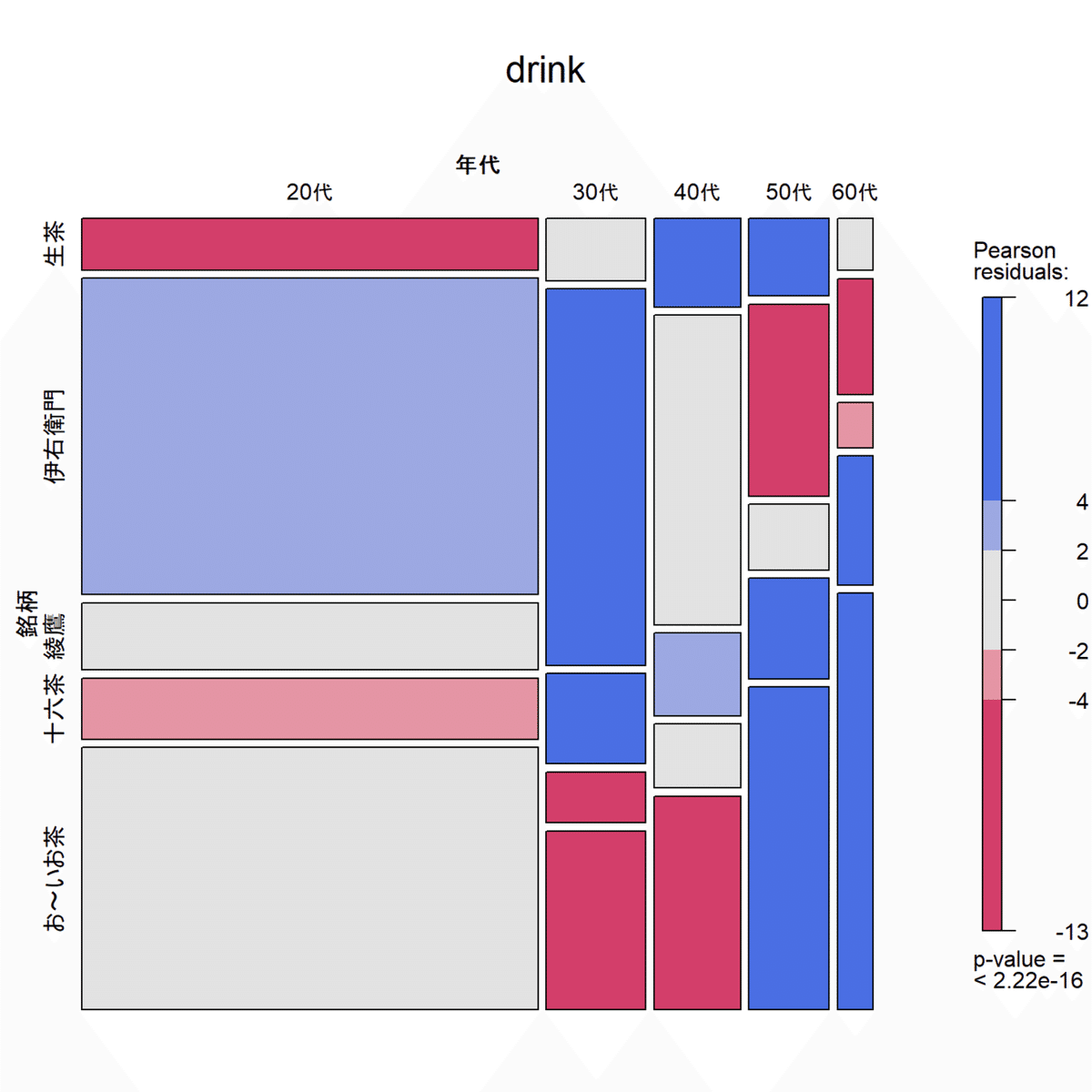
お疲れ様でした。
参考リンク
Understanding the Math of Correspondence Analysis
How to Interpret Correspondence Analysis Plots (It Probably Isn’t the Way You Think)
Correspondence Analysis: What is it, and how can I use it to measure my Brand? (Part 1 of 2)
Correspondence Analysis: What is it, and how can I use it to measure my Brand? (Part 2 of 2)
CA - Correspondence Analysis in R: Essentials
