効果量を踏まえたサンプルサイズ設計ツールを作りました!【統計的仮説検定】
こんにちは、青の統計学です。
前回、確率分布可視化ツールを作成し、かなり好評だったので、早速新しいシミュレーションツールを開発しました。
前回の記事↓
今回はサンプルサイズ設計ツールです
A/Bテストや機能改善の実験をするとき、みなさんは事前に「どのくらいのサンプル数が必要か」をしっかり設計しているでしょうか。
「とりあえずやってみて、何とか有意差が出たらOK」というスタンスだと、実際には本当に必要な効果が得られているのか曖昧になったり、長期間テストを引き伸ばして“偶然の有意差”を見つけてしまう(偽陽性)リスクが高まってしまいます。
そこでは、ビジネス上の意味合いを加味しながらサンプルサイズをシミュレーションできる新ツールを開発しました。今回は、このツールのコンセプトと機能、そしてサンプルサイズ設計にまつわる実務的なポイントを解説していきます。
サンプルサイズ設計ツールを作りました!パラメータを元に効果量を算出して、最低限必要なサンプルサイズを算出します。ビジネスでの説明がしやすいように、リフト値を変えると、グラフがヌルヌル動き、必要なサンプルサイズがどう変わるのかが視覚的にわかります。https://t.co/dpBT3xrlSV pic.twitter.com/qD0MmlP2qD
— 青の統計学-Data Science School- (@blue_statistics) February 5, 2025
ツールを見たい人は、こちらをどうぞ。
1. なぜサンプルサイズ設計が重要?
1.1 A/Bテストで陥りやすい問題
A/Bテストを実施するとき、事前に「どれくらいの差を検出したいか」や「どの程度の有意水準・検出力でテストを組むか」を決めず、勢いだけで走り始めることは少なくありません。すると、
偽陰性(Type IIエラー)
本当は差があったのに、サンプルが足りず「有意差なし」と判断してしまうリスク多重検定の乱発→偽陽性(Type Iエラー)のリスク増
「まだ有意差が出ないから、もうちょっとサンプルを集めよう」「そろそろ出たかな?」と何度も検定し、偶然の有意差を拾ってしまう
などの問題が起こりがちです。これではビジネス判断としても「本当に有効な施策なのか?」が分からなくなってしまいます。事前に必要サンプルサイズを設定しておくことは、こうした問題を回避し、テスト期間やコストを最適化するための大きなカギになります。
1.2 ビジネスで有意義な差とは何か?
実務では、「統計上の有意差を検出したい」だけでなく、その差がビジネス的に見て意味のある大きさかどうかが大切です。
たとえば、すでに磨き込みが進んでいる主要機能なら、1〜2%の改善でも十分に価値があるかもしれません。
逆に、まだ使用頻度が低い新機能であれば、10%程度の差がないと費用対効果が見合わない、という判断になるかもしれません。
このように、「最低限これくらいの差が出なければ実用的とはみなさない」ラインを明確に定め、その差分(リフト値)を検出できるだけのサンプルサイズを確保する、という考え方が重要になります。
とは、書いたものの「事前にこれくらいの効果は最低でも見たい」という最低限の目標値は決められないことがほとんどです。
ポジティブな施策であれば、とりあえずCTRが上がって欲しい。ネガティブな影響調査であれば、できるだけ効果は下がらないでほしい。なので、いちいちラインを決めるのは大変です。

なので、効果量の最低ラインvsサンプルサイズの関係を可視化することで、「これくらいまでならデータを集められるな」という事業側の判断を支援することができます。
2. ツールの概要──比率差のサンプルサイズをCohen’s hで設計
今回リリースしたツールでは、2群間の比率の差を検定したいケース(CTRやCVRなど、割合データを扱うA/Bテスト)に対応しています。背後では、Cohen’s hという効果量指標を用いてサンプルサイズを計算する仕組みを採用しました。
2.1 Cohen’s hとは
Cohen’s h とは、2群の比率差を標準化した指標で、
$${h = 2 \times \bigl(\arcsin(\sqrt{p_2}) - \arcsin(\sqrt{p_1})\bigr)}$$
の形で表されます。これにより、「実際に観測したい $${(p_2 - p_1)}$$ の幅が、統計学上どの程度インパクトのある違いか」を定量化できます。
2.2 サンプルサイズ計算式
有意水準 $${\alpha}$$、検出力$${(1 - \beta)}$$、そして上記Cohen’s h を用いると、必要サンプルサイズ $${n}$$ は下記のように近似されます。
$${n \approx 2 \times \frac{\bigl(z_{1-\alpha/2} + z_{1-\beta}\bigr)^2}{h^2}}$$
$${z_{1-\alpha/2}}$$: 両側検定で有意水準$${\alpha}$$に対応する標準正規分布の臨界値
$${z_{1-\beta}}$$: 検出力$${(1 - \beta)}$$に対応する標準正規分布の値
$${h}$$: 前述のCohen’s h
この式で算出されるのは2群合計のサンプルサイズ、もしくは両群それぞれに必要な数(分割比率が1:1のとき)に分割できるよう設計しています。
もちろん、WEBのA/Bテストなど、パキッとちょうど半分に分けられることは少ないですよね…
2.3 使い方はシンプル
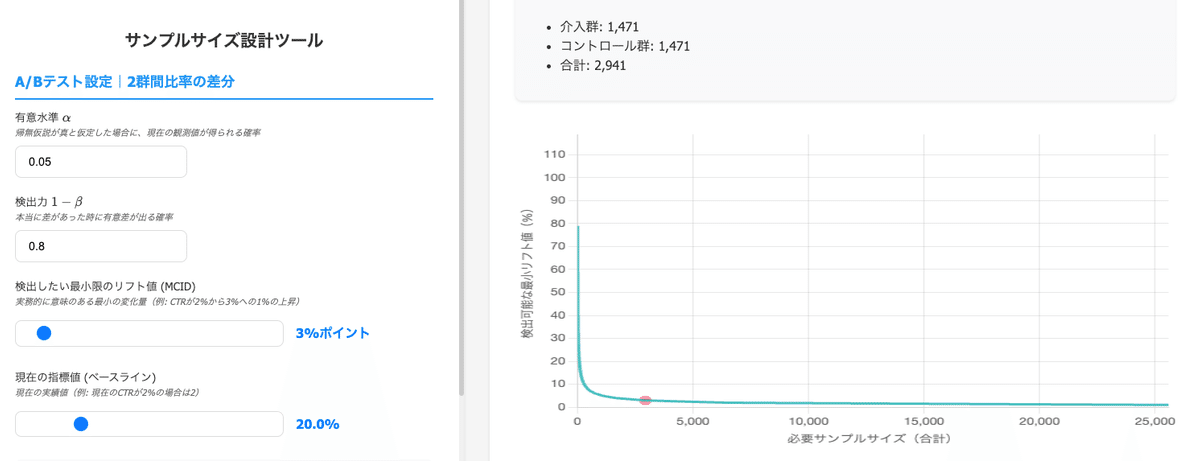
ツール画面では、以下の項目を入力すると、必要サンプルサイズとあわせてグラフが動的に変化します。
有意水準($${\alpha}$$)
例:0.05 (5%)
検出力($${1 - \beta}$$)
例:0.8 (80%)
検出したい最小限の差(リフト値)
例:現状CVR 20%を21%にしたい → +1pt
コントロール群の指標値
例:現状のCVR 20%
すると、必要サンプル数や計算根拠、注意事項などが表示され、グラフ上で「検出力と差の関係」が可視化されます(しかもぬるぬる動く!)。下記のように、数式や注意点もしっかり書かれているため、初学者でも無理なく使えるはずです。
3. 実務での使い方
3.1 小さな差を取りこぼさない
例えば、検索一覧画面や購入フローなど、ビジネスインパクトが大きい既存機能は既にCVRも高い場合が多いでしょう。そこで、わずか数%の改善でも大きな売上アップに繋がる可能性があります。
このときリフト値を小さめに設定すると、必要サンプルサイズは増えるものの、小さな変化も見逃さずに検知する確率が高まります。
3.2 新規機能で大きな差を狙う
逆に、まだ利用者が少なく、将来のポテンシャルを試す機能であれば、「10%以上の差がなければ大して有益ではない」という経営判断もありえます。そうした場合はリフト値を大きめに設定し、必要サンプルサイズが抑えられる形でテストを回せます。
時間やコストと相談しながら「どこまで小さな差を検出したいか」を調整できるのがポイントです。
3.3 実験期間や費用を事前に試算
また、1日あたりの流入UU数が限られている場合、「このサンプル数を集めるには何日くらい必要か」を見積もって計画を立てることができます。十分な期間が取れないのであれば、検出力や有意水準、リフト値をどう調整するかなど、意思決定層とすり合わせができます。
4.おまけ
4.1 注意していただきたい点
極端に小さい/大きい比率
母集団の比率 $${(p_1, p_2)}$$ が0%や100%に近いと、正規近似が崩れるリスクがあります。その場合は厳密には別の方法が必要になります。実装ルールを厳守
検証後の話ですが、途中経過でp値を何度もチェックして延長・打ち切りをする「Pハッキング」のような行為を行うと、多重比較の問題が発生し、検定結果の信頼性が失われます。ビジネス背景の把握
このツールはあくまで「どれくらいの差を検出したいか」を数字として入力する前提です。そこを曖昧にすると、計算結果だけが先走ってしまいかねません。
4.2 今後
今回のツールは「2群間の比率差」を扱うケースに注力していますが、今後は
連続値データ(平均値比較)を扱う検定
差分の差分 (DID) 手法のサンプルサイズ設計
多群比較や段階的ロールアウトに応用する方法
など、より幅広いシチュエーションにも対応できるようアップデートしていきたいと考えています。今までは数字と公式だけで敬遠されてきたサンプルサイズ設計を、ビジネスの現場でもサクッと使いこなせるツールへと進化させたいと思っています。
特に今回は、ビジネスで少しでも統計学を使って欲しく作成しました。
コストをかけてA/Bテストを回すのであれば、ぜひこの新ツールを活用してみてください。ビジネスサイドの方にもわかりやすく数値根拠を示せるので、「どれくらいテストする必要があるの?」という疑問に、しっかりした理屈で答えられるようになるはずです。
では、また。
いいなと思ったら応援しよう!

