
【無料】未来のデータサイエンティストのための機械学習と生成AI入門|G検定 E資格対策
こんにちは、青の統計学です。
青の統計学では、日々データサイエンスの専門性を磨けるコンテンツを配信しています。色々見てやってください。
WEB版:https://statisticsschool.com/
特徴:毎日更新、専門的な内容、
LINE版:https://lin.ee/jY1k9aj
特徴:限定特典、新着通知、アンケートや先行配信
note版:https://note.com/bluestatistics
特徴:チートシート、長めで専門的なコンテンツ、
X(旧Twitter版):https://x.com/blue_statistics
特徴:毎日更新、データサイエンス系の優良教材を紹介、スタッフアカウントもよろしくお願いします。
今回は、データサイエンティストを目指す方々へ向けての記事になります。
はじめに
この記事の目的
皆様は、統計検定やG検定、kaggle(データ分析コンペ)、各種教材を使った学習、ポートフォリオの作成など、日々目標に向けて努力しておられると思います。心から尊敬しています。
皆様の目標とは、単に資格を取得することではなく、その後の
「データサイエンティストになって、事業の意思決定を支援したい」
「データ分析業務に従事して、事業の課題や改善ポイントを見つけたい」
「転職活動のための武器や実績を作りたい」
「何か自分に強みが欲しい」
などなど、様々でしょう。
このような皆様を少しでも応援するために、今回はチートシートとは違った方向性のコンテンツを提供します。
この記事は、以下の方々におすすめです!
▪️データサイエンティストを目指す学生
▪️未経験からIT系に転職する社会人の方
▪️データ分析業務に携わりたい方
▪️これまで、漠然と資格取得を目指していたが、その先のキャリアへの活かし方や「どうビジネスでデータサイエンスを使うか」を学びたい方
▪️機械学習について、最近の生成AIまで外観をアルゴリズムなどの仕組みから知りたい方
▪️G検定やE資格に挑戦したい方
普段、青の統計学ではご覧の通り、
▪️情報数理を使った技術について
▪️統計的手法の詳しい使い方
▪️python等を使ったモデリング
など、を解説しています。
もちろん、テクニカルな知識はデータサイエンティストには必要不可欠なのですが、何らかの事業を担当する上では、技術力を発揮する前段階である、「課題発見力」や「ビジネスでデータサイエンスをどう活かすかを考える力」が本当に大切になってきます。
筆者自身、事業会社でデータサイエンティストをしており、このことを痛感しています。
この記事の使い方
使い方①
まず、ビジネスの現場でどのようにデータサイエンスや情報数理が必要な案件が生まれていくのかを説明します。
モチベーションがわかった上で、回帰や分類問題からディープラーニング、最後は大規模言語モデルまで説明を発展させて行こうと思います。
方法論のセクションでは、統計学や機械学習などの基礎的な知識が必要です。内容も突き詰めてちゃんとゴリゴリ数式も扱います。
そのため、以下のようなチートシートとは異なり、最初から順に読んでいただけると幸いです笑
使い方②
ビジネス応用の話の後に、機械学習について話を進めていきます。
詳しくは目次を見ていただければわかると思います。
各項目についての応用的な補足や証明については、別サイト「青の統計学-Data Science School-」の参考コンテンツを豊富に貼り付けておりますので、並行して学習に役立てていただければと思います。

お待たせしました!
今回も3万字を超える長編になっております。
きっと皆様の役に立つと思います。
ビジネスでデータサイエンスを使うということ
このセクションは記事の核心部分です。
ここを理解した上で、個別の方法論を学んでいただくだけで、大袈裟ですがその先の皆様の仕事の進め方はかなり良い方向に変わると思います。
このセクションで言いたいことは2つです!
①あくまでデータサイエンスは手段。
ビジネス課題を如何に整理し、その後スマートな手段に落とし込み、決裁まで進めませることが重要。
②データサイエンスやAIは魔法ではない。事業でデータ組織のプレゼンスを高めるために、価値のある案件を取捨選択しよう。
「すでに知っているよ!」と思いましたか?
①データサイエンスは手段
ありがちで且つ、よろしくない例で言うと
「データサイエンスを使うために、何か業務改善や施策をしたい!」
目的と手段が逆になっていますね。
ビジネスの現場ではよくハマってしまう罠なのですが、新しい技術や手法を使おうとするあまり、現場の課題感や原因をそれほど深掘りせずに案件が進んでしまうことがあります。
結果、提案が微妙で決裁がおりなかったり(まだマシ)、最悪の場合はプロジェクトが空中分解したり、プロダクトは作ったは良いものの、誰も使わなかった、などの結末を辿ることがあります。
では、将来のデータサイエンティストの皆様がどういうスタンスで案件に向き合えば良いかと言うと、
「チャットボットを作れば良いじゃん」
「Chat GPTを使いたい!」
「この推薦アルゴリズムを使いたい」
と、すぐに打ち手を考えるのはやめておきましょうということです。
結局打ち手として、データサイエンスを使うよりも良かった例は実はいくらでもあります。
例えば、ECサイトのポイントに有効期限をつけるだけで、売り上げが6%上がった例などがあります。
普段から統計や機械学習に触れていると、「ポイントをCSの期待購入額によって出すポイントを変えるモデルを作り、バンディット的に最適な額を最適化していく…」のように小難しく考えてしまいがちですが、まずは売り上げが伸びない背景や現状を整理するのが先なんですね。
さらにはシンプルであればあるほど、非ITの決裁者には伝わりやすい上に、デリバリー(案件リリース)まで早かったりします。
*元も子もない話ですが、我々がデータ分析をする以前のデータをモニタリングしたりする基盤(データマートなど)の整備ができていなかったりする事業もまだまだあります。
こうした事業だと、データをサイエンスするというよりは、泥臭くタグを埋め込んだり、BIツール(tableauなど)を導入したりするというのが、進み方としては合っています。
皆様が目指すデータサイエンティストとは、日々プロダクトに向き合う事業担当者とは異なります。なので、アサインされた当初はどうしても対象の解像度が低く、業務フローまで把握できていないことがほとんどです。
また、事業担当者も1から100まで教えてくれるわけではないので、
事業側の要求に対して、ビジネス課題がどこにありそうか?
その原因は何なのか
打ち手の方向性は?(要件が固まってきた!😆)
などを整理するために、ひたすらヒアリングや資料漁りをします。
WHY WHAT HOWとか色々フレーム枠がありますが、正直何でも良いです。
その後のフローですが、以下のようになっております。
打ち手として、どんな手法やロジックが選択肢としてあるか
改善幅の見立てを立てる(ざっくり!これがないと判断できない😭)
案件化!具体的な体制やスケジュールを決めていきます。
ここまできてようやく手段の話に入ります。
複雑なモデルを使った手段が適切なのか、ある特徴量を現状のモデルに入れるのが良いのか、もっとシンプルな話に落とし込める、などなど。
普段から勉強している個別の手法は、手段のうちの一つでしかないことを心がけてください。まずは、重要度の高い課題があり、それを整理した上で打ち手の議論ができます。
データサイエンティストといえば、常に機械学習ロジックと向き合ったり、論文を読んだりというイメージがあるかもしれません。
もちろんPoCの作成などはありますが、実態としては課題のヒアリングや業務フローの徹底理解のための資料漁り、基礎集計、決裁資料の作成などの業務もかなりウェイトを占めます。
②データサイエンスやAIは魔法ではない
統計学や機械学習を勉強している皆様には、釈迦に説法かもしれません。
例えば、
「来期の売り上げを予想して、A部署が持つ販促費用を決めたい」
と言う大変重要な案件があったとします。
データ部署が、時系列データの予測問題と捉え、ARモデルなどを作ったとしましょう。(参考リンクは下に置いておきます。)
ただ、実際はざっくりとした来年の市況トレンド(例えば、今期比+102.3%)を、単純に昨対の売り上げに掛けた方が精度が良かったです笑、なんてことはザラにあります。
稚拙な表現ですが、データサイエンスは綺麗なデータがいっぱいないと基本的には役に立ちません。(製造業だとガウス過程回帰など、少ないデータで精度ヨシのやり方も確立されているそうです。)
「モデルを作って、各プロダクトの予算配分を最適化して!」
「今よりもチャネルBのROIを精緻にみるために、AIを使いたい!」
非データ部署だと、上のようにどうしても「AIが何か解決してくれる!」と思ってしまいがちですが、実際AIでやる必要はなかったり、そもそもデータが取れていないので取ってから色々やりましょうね、という話で終わったりすることもあります。
我々はデータを使ってKPIを上げたり、利益貢献、業務支援をすることで価値を発揮します。いかにデータ部署でやるべき案件かを、かぎ分ける嗅覚とヒアリング力あたりが必要になってきます。よくわからない案件ばかり担当していると、成果が上げられません。
データ部署が社内で活躍していれば、「何をやっているか良くわからない数学好きの部署?」から「データを使って意思決定を支援してくれる部署」と見方が変わってくるはずです。
…さて、ここまで見てきましたが、振り返ると当たり前のことのように思えると思います。ただ、これが意外と難しいのです。
皆様が実際にデータサイエンス等の業務に従事するようになりましたら、少しでも思い出していただけると嬉しいです。
きっと役に立つはずです。
①あくまでデータサイエンスは手段。
ビジネス課題を如何に整理し、その後スマートな手段に落とし込み、決裁まで進めませることが重要。
②データサイエンスやAIは魔法ではない。事業でデータ組織のプレゼンスを高めるために、価値のある案件を取捨選択しよう。
機械学習と深層学習
さて、ビジネスにおけるデータサイエンスの立ち位置が理解できたところで、具体的な方法論の話になります。
機械学習のざっくりとした定義ですが、経験(つまりデータ)から学習することで、性能を改善していくプログラムのことです。
メジャーな分類の仕方としては、以下の3点です。
教師あり学習:入力$${x}$$に対して、出力$${y}$$のデータの関係性$${y=f(x)}$$を推定する
教師なし学習:入力データ集合$${X}$$の構造を同定する
強化学習:エージェントがある環境下で得られる報酬を最大化するような行動を選択するモデルを構築し、エージェントは試行錯誤を通じて最適な行動ポリシーを学習する。例えば、オセロなどのゲームにおけるNPCの行動選択は強化学習の典型例ですね
今回は、一般的な回帰や分類モデル→深層学習→言語モデル→NN言語モデル→生成AIという流れで解説していくので、教師なし学習と強化学習についてはそれほど触れません。
気になる方はこちらのコンテンツをご覧いただければと思います。
教師なし学習
強化学習
機械学習の目的
データサイエンティストがビジネスに機械学習モデルを使用する理由は、大きく二つに分けられます。それは、解釈性と予測精度です。
解釈性を求められつつ、精度良しとせねばなので、パキッと分けられる話ではないのですが、前者は特徴量間の関係性や目的変数にどの特徴量が貢献しているかを説明したいときに重視されます。
こちらは因果推論や計量経済、数理統計学の知識が必要です。
気になる方はこちらをご覧ください。
一方、後者は純粋に予測精度(指標はタスクによります)が高い結果を使って何かを運用または意思決定していきたいときに重視されます。ビジネスではないですが、kaggleが代表的ですね。
今回は後者の予測タスクに注目した記事です。
さて、教師あり学習では機械学習モデルがデータセット$${D}$$に含まれる$${(x,y)}$$の関係$${y=f(x)}$$を学習することで、未知の入力$${x}$$に対する予測値を推論することができます。
よく$${y=f(x)}$$はモデル、と呼ばれますが探索対象とする関数の空間を表しており、パラメータ$${\theta}$$を用いて記述されます。
このようなモデルをパラメトリックモデルと呼びます。
$${f(x;\theta)}$$
パラメータを明示的に記述しないモデルをノンパラメトリックモデルと呼びます。
さて、目先でやりたいことがビジネス課題の解決→モデルの構築→パラメータ$${\theta\in(w,b)}$$の推定と落とし込むことができました。$${w,b}$$はそれぞれ重みやバイアスです
では、どういったパラメータが最適でしょうか?
例えば、訓練データ$${D}$$に適合するようなモデル$${f}$$のパラメータは、モデルの予測と正解の誤差が小さくなるように調整を行うはずです。ここを目的関数と呼びます。
目的関数|平均二乗誤差とクロスエントロピー
ここでは二つの目的関数をご紹介します。
平均二乗誤差(mean squared error)
正解値$${y}$$と予測値$${\hat{y}=f(x)}$$の差の平方の平均のことです。
当然これは小さくなったほうが良いですね。
出力$${y}$$が連続値を取る時、つまり回帰問題などで使われる目的関数です。
$${E(y,\hat{y})=\frac{1}{N}\sum_{n=1}^{N}(\hat{y_n}-y_n)^2)}$$
こちらでも取り上げております。
クロスエントロピー誤差
各クラス$${k}$$における予測確率$${\hat{y_k}}$$と正解ラベル$${y_k}$$の近さの総和です。出力値$${y_{k}}$$が離散値を取るときに使われます。
$${E(y,\hat{y})=-\sum_{n=1}^N\sum_{k=1}^Klog\hat{y_{nk}}}$$
正解クラス$${k}$$に対する予測確率$${\hat{y_k}}$$を1に近づけたいと言うのがモチベーションです。分類問題において最も広く使われる損失関数の一つで、特に、二値分類問題に適用されます。この損失関数は、予測された確率が実際のラベルに近いほど小さくなります
最尤法
さて、機械学習におけるパラメータの推定方法は、最尤法に基づくものが多いです。
最尤法は、観測データに対して最も尤もらしいパラメータを推定する手法です。「一番頻度が多く観測されたデータが、真の確率分布でも最も生起確率が高い実現値だろう」という思想から来た考えです。結構納得しやすい考えなのではないでしょうか。
ここでは、頻度統計学の知識が必要です。
尤度に関して、基礎からしっかり学習したい方は以下のコンテンツをご覧ください。
尤度関数
そして尤度関数は、観測したデータが与えられた時のモデル(確率分布$${p_{\theta}}$$)の特定のパラメータ値がどれだけ尤もらしいかを示す関数です。
観測データを$${\mathbf{x}=(x_1,x_2,…,x_n)}$$、未知のパラメータを$${\theta}$$とします。データが独立同分布に従うと仮定すると、尤度関数 $${L(\theta;\mathbf{x})}$$ は次のように表されます
$${L(\theta;\mathbf{x})=p(\mathbf{x}|\theta)=\prod_{i=1}^{n}p(x_i|\theta)}$$
こちらを対数にして和の形にします。
対数尤度関数と呼びます。
$${\ell(\theta; \mathbf{x}) = \log L(\theta; \mathbf{x}) = \sum_{i=1}^n \log P(x_i|\theta)}$$
こちらを最大化するパラメータ$${\theta}$$を求めるので、一階微分をしてイコールゼロを解きます。最尤推定量(maximum likelihood estimator, MLE)は、対数尤度関数を最大化するパラメータ $${\theta}$$です。
$${\hat{\theta} = \arg\max_{\theta} \ell(\theta; \mathbf{x})}$$
補足|ガウス分布を例に最尤推定とMSEの関係
先ほど、基本的な機械学習タスクにおける目的関数はデータがカテゴリカルか連続値かによって、変わるという話をしました。
回帰問題:平均二乗誤差
分類問題:クロスエントロピー
ここが興味深い点なのですが、最尤法に基づく目的関数は平均二乗誤差と一致し、もちろんモデルがカテゴリ分布の場合は、最尤法の目的関数はクロスエントロピー誤差と一致します。
前者の平均二乗誤差と最尤法の目的関数について、データがガウス分布の場合を例にして考えて見ましょう。
モデルがガウス分布 $${ p_{\text{model}}(y|x) = \mathcal{N}(f(x; \theta), \sigma^2) }$$のとき、パラメータ $${\theta}$$ の対数尤度は以下のように変形できます。
$${ \log p_\theta(y|x) = \log \prod_{i=1}^N \frac{1}{\sigma\sqrt{2\pi}} \exp\left(-\frac{1}{2\sigma^2} (y_i - f(x_i; \theta))^2 \right) }$$
$${= \sum_{i=1}^N \log \frac{1}{\sigma\sqrt{2\pi}} - \frac{1}{2\sigma^2} \sum_{i=1}^N (y_i - f(x_i; \theta))^2 }$$
$${=-\frac{1}{2\sigma^2} \sum_{i=1}^N (y_i - f(x_i; \theta))^2 - \frac{N}{2} \log 2\pi\sigma^2}$$
このうち $${\theta}$$ に関わる第1項の $${\theta}$$ に関する最大化は、平均二乗誤差(の $${N}$$ 倍)の最小化に対応します。
ロジスティック回帰
ロジスティック回帰(Logistic Regression)は、分類問題における代表的な線形モデルの一つです。
主に二値分類(二項分類)問題で使用されますが、多クラス分類(多項分類)問題にもソフトマックス関数を使えば拡張可能です。
順に見ていきましょう。
ロジスティック回帰は、データポイントがあるクラスに属する確率をモデル化します。具体的には、確率を0から1の範囲に収めるために以下のようなシグモイド関数(ロジスティック関数)を使用します。
$${\sigma(z) = \frac{1}{1 + \exp(-z)}}$$
$${z}$$は入力ベクトルの線型結合ですね。
$${z = \mathbf{w}^\top \mathbf{x} + b}$$

ロジスティック回帰では、クラス1に属する確率 $${P(y=1∣\mathbf{x})}$$ を次のようにモデル化します
$${P(y=1|\mathbf{x}) = \sigma(\mathbf{w}^\top \mathbf{x} + b) = \frac{1}{1 + \exp(-(\mathbf{w}^\top \mathbf{x} + b))}}$$
クラス0に属する確率$${P(y=0∣\mathbf{x})}$$ は次のように表されます
$${P(y=0|\mathbf{x}) = 1 - P(y=1|\mathbf{x})}$$
さて、ロジスティック回帰のモデルパラメータ $${\mathbf{w}}$$ と $${\mathbf{b}}$$ を学習するために、対数尤度を最大化します。
二項分類問題の対数尤度は次のように定義されます
$${\ell(\mathbf{w}, b) = \sum_{i=1}^N \left[ y_i \log \sigma(\mathbf{w}^\top \mathbf{x}_i + b) + (1 - y_i) \log (1 - \sigma(\mathbf{w}^\top \mathbf{x}_i + b)) \right]}$$
対数尤度を最大化することは、負の対数尤度を最小化することと等価です。
$${L(\mathbf{w}, b) = -\ell(\mathbf{w}, b) = -\sum_{i=1}^N \left[ y_i \log \sigma(\mathbf{w}^\top \mathbf{x}_i + b) + (1 - y_i) \log (1 - \sigma(\mathbf{w}^\top \mathbf{x}_i + b)) \right]}$$
ロジスティック回帰の学習|勾配降下法
さて、上のセクションで対数尤度関数をパラメータについて微分してイコール0を解く、と言う話をしましたが、それは基本的な確率分布だからできる話であり、実データを使った尤度関数だとなかなか解析的に最尤推定量を求めるのは難しいのです。
探索的にパラメータを求めたい場合に使われるのが勾配降下法です。
この辺りの考え方は、MCMC(ベイズ推定で使われるパラメータ探索手法)などの直感的理解にもつながるので、しっかりと学習してほしいです。
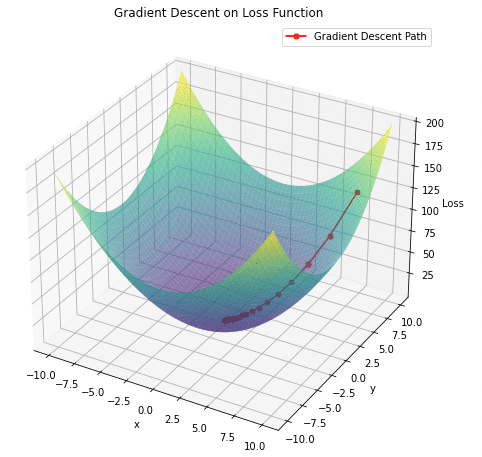
上の図のように、目的関数が小さくなるようなパラメータを少しずつ探っていく方法です。
パラメータ$${\mathbf{w}}$$の勾配更新
$${\frac{\partial L}{\partial \mathbf{w}} = \sum_{i=1}^N (\sigma(\mathbf{w}^\top \mathbf{x}_i + b) - y_i) \mathbf{x}_i}$$
$${\mathbf{w} \leftarrow \mathbf{w} - \eta \frac{\partial L}{\partial \mathbf{w}}}$$
ここの$${\eta}$$は学習率といい、これを大きくすればするほど、空間内の一回の探索幅が大きくなり、学習が収束に近づきますが、安定しません。逆に小さいと、学習が終わらないし、局所解に陥ることがあります。学習率は初期設定に依存し、適切な値を選定するためには経験的なアプローチが必要です。
イメージとしては、ちょっと凹んだ部分が目的関数の最小値だと思いこみ、そこからぐるぐる抜け出せない状態です(伝わってほしい)

少し上の図だと分かりにくいのですが、最も損失関数が低い部分ではなくその横あたりで探索が終了していることがわかります。これなんかは、二次関数にsin関数を追加することで、複数の局所最小値を持つ関数を簡単に作成できます。
つまり、適切なパラメータ(目的関数を最小値にする、は無理でもそれに極めて近い値)を求めるには学習率、更新の速度をうまく調整する必要があります。
バイアス$${\mathbf{b}}$$についても同じですね。
$${\frac{\partial L}{\partial b} = \sum_{i=1}^N (\sigma(\mathbf{w}^\top \mathbf{x}_i + b) - y_i)}$$
$${b \leftarrow b - \eta \frac{\partial L}{\partial b}}$$
さて、ロジスティック回帰の理解は進みましたでしょうか。実務でも多く使われているので、しっかり身につけてほしいです。k=2を超えるカテゴリの場合はシグモイド関数ではなく、ソフトマックス関数を使うので、ご注意ください。
青の統計学では、ロジスティック回帰について多めに取り扱っております。
補足|ミニバッチ勾配降下法とエポック
さて、局所解から抜け出す方法の一つとして、ミニバッチ勾配降下法があります。
ミニバッチ勾配降下法は、トレーニングデータを小さなバッチ(ミニバッチ)に分割し、各バッチに対して勾配を計算してパラメータを更新します。以下は手順です。
トレーニングデータをシャッフル
トレーニングデータをバッチサイズ $${m}$$ に分割
各バッチに対して以下の操作を行う
勾配を計算
パラメータを更新
手順1の部分、サンプリングの過程でランダムネスが入るため、局所解から抜け出しやすいです。
バッチサイズを $${m}$$ とすると、ミニバッチ $${\mathcal{B}}$$ における損失関数は次のように定義されます
$${L_{\mathcal{B}}(\mathbf{w}, b) = -\frac{1}{m} \sum_{i \in \mathcal{B}} \left[ y_i \log \sigma(\mathbf{w}^\top \mathbf{x}_i + b) + (1 - y_i) \log (1 - \sigma(\mathbf{w}^\top \mathbf{x}_i + b)) \right]}$$
これに基づく勾配更新は次のように計算されます。
順に重み$${w}$$バイアス$${b}$$です。
$${\frac{\partial L_{\mathcal{B}}}{\partial \mathbf{w}} = \frac{1}{m} \sum_{i \in \mathcal{B}} (\sigma(\mathbf{w}^\top \mathbf{x}_i + b) - y_i) \mathbf{x}_i}$$
$${\mathbf{w} \leftarrow \mathbf{w} - \eta \frac{\partial L_{\mathcal{B}}}{\partial \mathbf{w}}}$$
$${\frac{\partial L_{\mathcal{B}}}{\partial b} = \frac{1}{m} \sum_{i \in \mathcal{B}} (\sigma(\mathbf{w}^\top \mathbf{x}_i + b) - y_i)}$$
$${b \leftarrow b - \eta \frac{\partial L_{\mathcal{B}}}{\partial b}}$$
パラメータの更新後に検証データでモデルの性能を評価します。そして、ハイパーパラメータであるエポック数に応じて、上の手順を繰り返します。
*エポック(epoch)は、全てのトレーニングデータが一度モデルを通過することを指します。エポックが完了するごとに、モデルはデータ全体を一度見て学習することになります。深層学習だと通常、複数のエポックを通してモデルをトレーニングし、収束を目指します。
ちなみに、当然エポック数が増えれば増えるほど過学習の懸念が増すので、言語モデルの事前学習のエポック数は基本1回です。
多層パーセプトロンと深層学習
多層パーセプトロン(MLP: Multi-Layer Perceptron)は、ニューラルネットワークの一種であり、非線形データの分類や回帰問題を解くために広く用いられています。
このセクションでは、MLPの構造、学習方法、およびその数理的背景について詳しく説明します。ロジスティック回帰を理解できていればきっと大丈夫です。
先ほど、ロジスティック回帰の部分で以下のようなモデルを仮定しました。
$${P(y=1|\mathbf{x}) = \sigma(\mathbf{w}^\top \mathbf{x} + b) = \frac{1}{1 + \exp(-(\mathbf{w}^\top \mathbf{x} + b))}}$$
活性化関数としてシグモイド関数を置いておりますが、これが実は単純パーセプトロンと言う、入力と出力のみからなるモデルなのです。

対して、多層パーセプトロン(MLP)は、入出力の間に隠れ層という複数の層を入れております。これは入力と出力の間の非線形な関数をモデル化しようというモチベーションからきています。

MLPは以下の要素から構成されます。
入力層(Input Layer):入力データを受け取る層。
隠れ層(Hidden Layers):入力層と出力層の間にある層。1つ以上の隠れ層を持つことができます。層の数を深さ(depth)と呼びます。
出力層(Output Layer):最終的な予測結果を出力する層。
各層は複数のニューロン(ノード)を持ち、隣接する層のニューロンと完全に結合(全結合)されています。
ニューロンの計算
第 $${l}$$層の第 $${j}$$ ニューロンの出力は次のように表されます
$${z_j^{(l)} = \sum_{i} w_{ij}^{(l)} a_i^{(l-1)} + b_j^{(l)}}$$
$${z_j^{(l)}}$$:第$${l}$$層の第$${j}$$ニューロンの総入力
$${w_{ij}^{(l)}}$$:第$${l}$$層の第$${j}$$ニューロンの重み
$${a_i^{(l-1)}}$$:前の層の第$${i}$$ニューロンの出力(活性化)
$${b_j^{(l)}}$$:バイアス
活性化関数
次に、活性化関数 $${\sigma}$$ を適用して出力を計算します
$${a_j^{(l)} = \sigma(z_j^{(l)})}$$
活性化関数にはいくつかの種類があります。
シグモイド関数:$${\sigma(z) = \frac{1}{1 + \exp(-z)}}$$
ReLu関数:$${\sigma(z) = \max(0, z)}$$
tanh関数:$${\sigma(z) = \tanh(z)=\frac{e^{h}-e^{-h}}{e^h+e^{-h}}}$$
以下の記事で詳しく扱っています。
順伝播
MLPでは、入力データが入力層から出力層に向かって伝播します。第 $${l}$$層のニューロンの出力を $${a(l)}$$とすると、入力層の順伝播は以下になります。
$${a_i^{(1)} = x_i \quad \text{(入力データ)}}$$
当然そのまま入力ベクトルが入ります。
隠れ層では、
$${z_j^{(l)} = \sum_{i} w_{ij}^{(l)} a_i^{(l-1)} + b_j^{(l)}}$$
後述する部分ですが、誤差逆伝播法でこの重み$${\mathbf{w}}$$とバイアス$${\mathbf{b}}$$が更新されます。
出力層では、
$${a_j^{(l)} = \sigma(z_j^{(l)})}$$
シグモイド関数を例として載せています。これはタスクによりますが、最後に出力するのが、カテゴリ3以上の確率であればソフトマックス関数を通すことになります。
誤差逆伝播法
さて、単層ではできなかったパラメータ更新の方法についてです。
ここが深層学習で最も特徴的かつ大事な部分です。誤差逆伝播法を使用して重みとバイアスを更新します。具体的には、損失関数の勾配を計算し、それに基づいてパラメータを更新する手法です。
損失関数として一般的に使用されるのは平均二乗誤差(MSE)やクロスエントロピーです。
ここでは、クロスエントロピー損失を用います。
$${y_i}$$は実際のラベルで、$${\hat{y_i}}$$は予測したラベルです。
$${L = -\sum_{i=1}^N \left[ y_i \log \hat{y}_i + (1 - y_i) \log (1 - \hat{y}_i) \right]}$$
出力層の誤差
当然ですが、出力層のニューロンの誤差は予測された出力$${a_j^{(L)}}$$と実際のラベル$${y_j}$$の差として計算されます
$${\delta_j^{(L)} = a_j^{(L)} - y_j}$$
隠れ層の誤差
隠れ層のニューロンの誤差は、次の層の誤差と重みに基づいて計算されます。第 $${l}$$ 層の第 $${j}$$ ニューロンの誤差は以下のように計算されます
$${\delta_j^{(l)} = \left( \sum_{k} w_{jk}^{(l+1)} \delta_k^{(l+1)} \right) \sigma'(z_j^{(l)})}$$
$${w_{jk}^{(l+1)}}$$:$${l+1}$$ 層の第 $${k}$$ ニューロンから第 $${l}$$ 層の第 $${j}$$ニューロンへの重み
$${\delta_k^{(l+1)}}$$:$${l+1}$$ 層の第 $${k}$$ ニューロンの誤差
$${\sigma'}$$はシグモイド関数の導関数です。
$${\sigma'(z) = \sigma(z)(1 - \sigma(z))}$$
この導関数が小さすぎると、勾配が消失してパラメータ更新がうまく行かない場合があります。なので、導関数が小さくなりすぎないrelu関数を使うことが多いです。
詳しくは、RNN(リカレントニューラルネットワーク)の部分で補足しているのでご覧いただければと思います。
パラメータの更新
重みとバイアスの更新は、先ほど説明した勾配降下法に基づいて次のように行います
$${w_{ij}^{(l)} \leftarrow w_{ij}^{(l)} - \eta \delta_j^{(l)} a_i^{(l-1)}}$$
$${b_j^{(l)} \leftarrow b_j^{(l)} - \eta \delta_j^{(l)}}$$
$${\delta_j^{(l)}}$$:第 $${l}$$ 層の第 $${j}$$ ニューロンの誤差
$${a_i^{(l-1)}}$$:前の層の第 $${i}$$ ニューロンの出力
パラメータを更新していく過程は分かりましたが、初期値は一様分布やガウス分布からサンプリングした値にしたり、やり方はさまざまです。
$${\theta_i \sim U(a, b),\theta_i \sim \mathcal{N}(\mu, \sigma^2)}$$
他にも、Xavier初期化と呼ばれる方法だと、以下のような一様分布からサンプリングします。
$${\theta_i \sim U\left(-\sqrt{\frac{6}{n_{in} + n_{out}}}, \sqrt{\frac{6}{n_{in} + n_{out}}}\right)}$$
$${n_{in}}$$ は前の層のユニット数、$${n_{out}}$$ は次の層のユニット数です。この初期化方法は、シグモイド関数やtanh関数を活性化関数として使用する場合に効果的です。
補足|最適化手法モメンタムやAdamについて
さて、ロジスティック回帰の部分でも扱った勾配降下法の学習率$${\eta}$$について、学習中は常に一律で良いのか?という疑問があると思います。
「初期は大きく動いて、損失関数の値が小さい領域を探したい」
「学習終盤では、細かく動いて、極小値を探したい」
など、学習のプロセスの中で探索の方針が変わると思います。こうしたモチベーションで作られたのが最適化手法です。
モメンタム
モメンタムは、過去の勾配の移動平均(勾配の一次モーメント)を考慮に入れて現在の更新に適用します。これにより、勾配の変動を滑らかにし、谷の底に速く到達するのに役立ちます。
通常の勾配降下法の更新式は以下のようになります。
$${\Delta \theta^{(t)} = -\eta \nabla E(\theta^{(t-1)})}$$
モメンタム項を加えます
$${\Delta \theta^{(t)} = -\eta \nabla E(\theta^{(t-1)}) + \gamma \Delta \theta^{(t-1)}}$$
モメンタム法では、前回の更新量 $${Δ\theta(t−1)}$$ を用いて、勾配の方向が変わる際に行き過ぎないようにします。
項の正負に注目すると以下のような特徴があることがわかります。
収束の加速:同じ方向に進んでいるときには勢いがつくため、谷の底に速く到達する。
振動の抑制:勾配の方向が変わる際に行き過ぎないようにすることで、収束の安定性が向上する。
Adam
Adamはモメンタムのように勾配の一次モーメント(移動平均)を使用し、さらに勾配の二次モーメント(分散)も考慮します。これにより、勾配の大小に応じて学習率を適応的に調整することができます
具体的に見ていきましょう。
初期化
$${g_i^{(t)} = \nabla E(\theta_i^{(t)}), \quad m_i^{(0)} = 0, \quad v_i^{(0)} = 0}$$
一次モーメント(移動平均)は次のように更新されます
$${m_i^{(t)} = \beta_1 m_i^{(t-1)} + (1 - \beta_1) g_i^{(t)}}$$
二次モーメント(移動平均の二乗)は次のように更新されます
$${v_i^{(t)} = \beta_2 v_i^{(t-1)} + (1 - \beta_2) (g_i^{(t)})^2}$$
$${\beta_1,\beta_2}$$はそれぞれ、一次・二次モーメントの減衰率です。
バイアス補正
バイアス補正を行うことで、初期ステップにおけるバイアスを軽減します。
→これがないと、$${m,v}$$が0付近に偏ってしまうイメージです。
補正された一次モーメントと二次モーメントは次のように計算されます
$${\hat{m}_i^{(t)} = \frac{m_i^{(t)}}{1 - \beta_1^t}}$$
$${\hat{v}_i^{(t)} = \frac{v_i^{(t)}}{1 - \beta_2^t}}$$
二次モーメント(移動平均の二乗)は次のように更新されます。
$${\Delta \theta_i^{(t)} = -\alpha \frac{\hat{m}_i^{(t)}}{\sqrt{\hat{v}_i^{(t)}} + \epsilon}}$$
深層学習の勾配降下法の最適化手法では、基本的にこのAdamが用いられています。
補足|ノルムと正則化
隠れ層を深くすればするほど、データの特徴を反映したパラメータを推定することはできますが、一方で訓練データに対して過剰に適合したモデルになり、かえって汎化性能(未知のデータの予測性能)は落ちる懸念があります。
正則化(Regularization)は、こうしたモデルの過学習を防ぐための技術です。基本的な目的としては、モデルの複雑さを制約することで、より汎用的なモデルを構築することです。
まず前提として、ノルムの定義に触れましょう。
線形代数を習った方なら聞き覚えがあると思います。
ベクトル$${\mathbf{v}=(v_1,…,v_n)}$$ について、 $${\mathbf{v}}$$ の$${L_p}$$ ノルムは次のように定義されます
$${|| v ||_p = ({v_1}^p + \cdots + {v_n}^p)^{1/p}}$$
ここでは、L2(p=2)とL1(p=1)の2種類をご紹介します。
L2正規化
L2正則化項は以下のように定義されます。下の2は添え字なのであまり気にしないでください。
$${\Omega(\theta) = \frac{1}{2} | |w| |_2^2}$$
重みが大きくなればなるほど、ペナルティが大きくなり、損失関数が大きくなると考えればOKです。勾配降下法は損失関数が小さいほうに探索していくので、重みが大きくなりすぎるとそのパラメータは取らなくなります。
正則化された目的関数は以下のようになります。
$${\alpha}$$が正則化パラメータですね。当然ですが、これはハイパーパラメータにあたるので分析者が事前に決めるか、ハイパラ探索をする必要があります。
$${\tilde{J}(w; X, y) = J(w; X, y) + \frac{1}{2} \alpha || w ||_2^2}$$
L2正則化の勾配は以下のように決定されます。
$${\nabla_w \tilde{J}(w; X, y) = \nabla_w J(w; X, y) + \alpha w}$$
この正則化を使った回帰はリッジ回帰と呼びます。基本的な回帰タスクでも使われる手法ですので、正則化手法は理解しておく価値が高いです。こちらもどうぞ。
L1正則化
L1正則化は、パラメータのL1ノルムを用いる正則化手法です。L1正則化は、多くのパラメータをゼロにすることで、モデルをスパースな状態にします。これにより、重要な特徴の選択が行われます。
$${\Omega(\theta) = || w ||_1 = \sum{i} ||w_i||}$$
正則化された目的関数は以下のようになります。
$${\tilde{J}(w; X, y) = J(w; X, y) + \alpha || w ||_1}$$
L1正則化の勾配は以下のように決定されます。
$${\nabla_w \tilde{J}(w; X, y) = \nabla_w J(w; X, y) + \alpha \text{sign}(w)}$$
$${sign(w)}$$ は $${w}$$ の符号関数です。
L1正則化はL2正則化と比較してスパースな解が得られます。すなわち、多くのパラメータの最適値が0となります(もしくは0に近づきます)。
こうしたL1正則化におけるスパース性は、特徴量選択のメカニズムとして広く用いられています。とりあえず、交互作用項を増やしてL1正則化で特徴量を減らしていく、みたいなやり方がkaggleであったりします。
L1正則化項を使った手法は、ラッソ(Lasso)回帰と呼びます。
こちらの記事もどうぞ。
さて、最後に視覚的にふたつのノルムを比較してみましょう。

L1ノルム(左側のプロット):ダイヤモンド型の等高線が描かれます。座標軸に沿って変化することを示しています。
L2ノルム(右側のプロット):円形の等高線が描かれます。すべての方向に対して等しく変化することを示しています。
これらの正則化手法は一般的に重み減衰(weight decay)として知られ、重みを原点に近づける効果があります。重み減衰項の追加によって学習則が変更され、通常の勾配の更新が行われる直前にステップごとに一定の割合で重みベクトルが減少します。
ニューラルネットワーク周りの他のモデルやpythonでの実装例まで知りたい方は、青の統計学の以下の記事をご覧になるのが良いかと思います。
生成AIとTransformer
ここからは、言語モデルのセクションです。
言語モデル|自己回帰モデル
昨今ChatGPTやGemini、Llamaなどの多くの大規模言語モデルがリリースされており、テキストや画像、音声、動画などをプロンプト(ユーザーが入力する命令文)を元に生成することができます。
そのクオリティも日毎に上がっていき、人間の作品なのか生成画像なのかはもはや見分けがつかないです。
ただ、生成AIすごい!と驚いてばかりではなく、裏側のアルゴリズムやできることやできないこと、課題などをしっかり把握することが、皆様にとっては大事なはずです。
生成AIの核である「言語モデル」から考えていきましょう。
さて、言語モデルは端的にいえば、ある単語の系列$${x_1,x_2,…,x_n}$$(文章でOKです)の生成確率$${p(x_1,x_2,…x_n)}$$(どれくらい発生しやすいか)をモデル化したものです。
例えば、ある質問に続く答えを推論するのがQAタスクになります。また、ある言語に続いて、ふさわしい他の言語は?と推論するのが翻訳タスクになります。
生成確率$${p(x_1,x_2,…x_n)}$$は同時分布になっています。
これを連鎖律を使って、条件付き確率の積の形で分解してあげます。
$${p(x_1,x_2,…x_n)=p(x_1)p(x_2|x_1)…p(x_{n}|x_1,x_2,…,x_{n-1})}$$
上のようなモデルを自己回帰言語モデルと呼びます。
何が嬉しいかというと、$${x_k}$$までの系列が所与のときに$${x_{k+1}}$$として確率が最も高いものは…と生成タスクを解くことができます。
各条件付き確率は、モデルの一部として逐次的に計算されます。自己回帰モデルの典型的な例として、リカレントニューラルネットワーク(RNN)があります。RNNは、時間的なデータを処理するのに適しており、時系列データや自然言語処理に広く使用されます。次のセクションで詳しく扱います。
RNN|自己回帰言語モデル
ここでは、リカレントニューラルネットワーク(RNN)の解説をします。
多層パーセプトロンや深層学習のパイプラインが理解できていれば大丈夫です。RNNは、代表的なモデルとしてSeq2Seqがあり、冒頭の単語から一単語ずつニューラルネットワークに入力し、ニューロンを逐次更新するモデルです。
まずモデルのモチベーションを確認しましょう。RNNの学習は、与えられた入力シーケンスに対して出力シーケンスを生成し、その予測と実際の値との誤差を最小化することを目的とします。

上の図は、入力した文章「明日の天気はなんですか?」等が、トークンに分けられて、デコーダから出力される様子です。
これまで説明してきた通常のニューラルネットワークと同様に、誤差逆伝播法(Backpropagation)を用いて勾配を計算し、勾配降下法(Gradient Descent)によりパラメータ(重みとバイアス)を更新します。
RNNの特徴としては、以下3点です。
逐次的な処理:RNNは系列(シーケンス)データを逐次的に処理し、各タイムステップで前の隠れ状態を考慮に入れます。一単語ずつ入力するということですね。
隠れ状態の更新(一番の特徴!):各タイムステップ $${t}$$ における隠れ状態 $${h_t}$$ は、前のタイムステップの隠れ状態$${h_{t−1}}$$ と現在の入力 $${x_t}$$ に基づいて更新されます。
$${h_t=tahn(W_{hh}h_{t-1}+W_{xh}x_i+b_h)}$$
$${h_t}$$:タイムステップ$${t}$$における隠れ状態ベクトル
$${x_t}$$:タイムステップ$${t}$$における入力ベクトル
$${W_{hh}}$$:隠れ状態間の重み行列
$${W_{xh}}$$:入力から隠れ状態へのの重み行列
$${b_{h}}$$:バイアス項
$${tanh_{h}}$$:双曲線正接関数(非線形活性化関数)
活性化関数については、色々とあるので以下のコンテンツを見ていただくのが良いです。
出力の生成:各タイムステップの出力 $${y_t}$$ は隠れ状態に基づいて計算されます。
$${y_t=W_{hy}h_{t}+b_y}$$
$${W_{hy}}$$:隠れ状態から出力へのの重み行列
$${b_{y}}$$:バイアス項
RNNの他にも、以下のようなモデルがあります
LSTM:long short term memoryと呼ばれるモデルで、RNNのモデルに加えて忘却ゲートとセルを用意して、長期的な依存関係を学習できるようにしています。
GRU :gated recurrent unit と呼ばれるモデルで、リセットゲートと更新ゲートの2つのみを使用して、LSTMのセルの機能を隠れ状態が担うようにしているという、シンプルなモデルです。
この二つは、あまりにも長くなってしまうため割愛させていただきます。
補足|勾配消失と勾配爆発の仕組み
さて、ここまで言語モデルや隠れ層を増やしたニューラル言語モデルを扱ってきましたが、以下のような課題があります。
①長期依存関係の学習の難しさ
特にRNNは長いシーケンスにおいて勾配が消失または爆発するため、長期依存関係を学習するのが難しいです。LSTMやGRUはこの問題を部分的に解決しますが、完全には克服できない場合もあります。
なぜ、勾配が消失するのでしょうか?
考えてみましょう。
上で見た、隠れ状態の更新式は以下のとおりです。
$${h_t = \tanh(W_{hh} h_{t-1} + W_{xh} x_t + b_h)}$$
RNNの学習は、誤差逆伝播法(BPTT: Backpropagation Through Time)を用いて行われます。損失関数 $${L}$$に対するパラメータ $${\theta}$$ の勾配を計算するために、連鎖律を使用します。
まず、重み$${W_{hh}}$$に対する勾配を計算します。
$${\frac{\partial L}{\partial W_{hh}} = \sum_{t=1}^T \frac{\partial L}{\partial h_t} \frac{\partial h_t}{\partial W_{hh}}}$$
ここで、各タイムステップにおいて隠れ状態の勾配$${\frac{\partial h_t}{\partial W_{hh}}}$$を求めるために、時間方向に逆方向に連鎖律を適用させます。
次に、隠れ状態$${h_t}$$の勾配$${\frac{\partial h_t}{\partial W_{t-1}}}$$を考えます。上の隠れ状態の更新式を微分したら良いので、
$${\frac{\partial h_t}{\partial h_{t-1}} = \left(1 - \tanh^2(W_{hh} h_{t-1} + W_{xh} x_t + b_h)\right) W_{hh}}$$
また、活性化関数の微分は以下なので、
$${\frac{\partial tanh(x)}{\partial x}=1-tanh^2(x)}$$
$${h_t}$$における勾配はわかりました。
$${\frac{\partial h_t}{\partial h_{t-1}} = \left(1 - \tanh^2(W_{hh} h_{t-1} + W_{xh} x_t + b_h)\right) W_{hh}}$$
とはいえ、タイムステップは1からなので、1まで連鎖律を適用させて、あるタイムステップ $${t}$$における勾配を、時間 $${t}$$から始まるすべての後続の勾配の積として表現できます。(これが誤差逆伝播)
$${\frac{\partial L}{\partial h_t} = \frac{\partial L}{\partial h_{T}} \prod_{k=t}^{T-1} \frac{\partial h_{k+1}}{\partial h_{k}}}$$
ここが原因ですね。
簡単のために、非線形部分を切り出して下のように近似させます。
連鎖律を使うと積の形で表されることがわかります。
右辺の行列式の固有値の絶対値が1未満か1以上の場合、値がどんどん小さくor大きくなっていくことがわかります。
$${\left| \prod_{k=t}^{T-1} \frac{\partial h_{k+1}}{\partial h_{k}} \right| \approx \left| W_{hh} \right|^{T-t} \quad \text{with} \quad | W_{hh} | < 1}$$
$${\left| \prod_{k=t}^{T-1} \frac{\partial h_{k+1}}{\partial h_{k}} \right| \approx \left| W_{hh} \right|^{T-t} \quad \text{with} \quad | W_{hh} | > 1}$$
この辺りを完全に理解するには、線形代数(固有値や対角行列まわり)の知識が必要です。こちらをご覧いただければと思います。
さて、行列 $${W_{hh}}$$ の固有値の絶対値が1未満または1を超える場合に、それぞれ勾配消失や勾配爆発が発生することがわかりました。
もう少し単純な言い方をすると、ネットワークが単語方向に深くなるため、学習が不安定になるということですね。最初の方の入力まで、誤差を逆伝播するのが大変なのです。構造上しょうがないという面もあります。
②逐次処理による非効率性
RNN、LSTM、GRUはシーケンスを逐次的に処理するため、並列計算が難しく、学習速度が遅くなる傾向にあります。
③固定長の隠れ状態
RNNは固定長の隠れ状態に情報を圧縮する必要があり、複雑な情報を十分に表現するのが難しいです。
言語モデル|エンコーダ・デコーダモデル
自己回帰言語モデルの他にも、もう一つの主要なアプローチとして、エンコーダ・デコーダモデルがあります。エンコーダ・デコーダモデルは、特に機械翻訳や要約生成などのシーケンスからシーケンスへの変換タスクにおいて強力な性能を発揮します。
エンコーダとデコーダについて、聞き慣れないという方はこちらの記事でオートエンコーダの知識を入れてからの方が良いと思います。
ざっくり言うと、エンコーダは入力データを内部表現(潜在空間表現)に変換、デコーダは内部表現を元の入力データを再構築(再構成)する機構です。
エンコーダ・デコーダモデルは、エンコーダ部分が入力シーケンスをコンパクトな表現(コンテキストベクトル)に変換し、デコーダ部分がその表現を元に出力シーケンスを生成する仕組みです。
まず、入力シーケンス$${(x_1,x_2,…,x_n)}$$に対して、エンコーダはそれぞれの単語をベクトル表現に変換し、これらのベクトルを順番に入力として受け取ります。エンコーダの出力は以下のように表されます。
$${h_t=Encoder(x_t,h_{t-1})}$$
ここで$${h_t}$$は時刻$${t}$$における隠れ状態、$${x_t}$$は入力シーケンスの$${t}$$番目の要素です。
エンコーダの最終隠れ状態$${h_n}$$は、コンテキストベクトル$${c}$$としてデコーダに渡されます。
次に、デコーダはこのコンテキストベクトルを受け取り、逐次的に出力シーケンス$${(y_1,y_2,…,y_m)}$$を生成します。デコーダの各時刻における出力は以下のように計算されます。
$${s_t=Decoder(y_{t-1},s_{t-1},c)}$$
ここで、$${s_t}$$は時刻$${t}$$におけるデコーダの隠れ状態、$${y_{t−1}}$$は$${t−1}$$番目の出力です。
また、デコーダは各時刻において次の単語の確率分布を計算します。
$${𝑝(𝑦_𝑡∣𝑦_1,…,𝑦_{𝑡−1},𝑐)=softmax(𝑊_{𝑠_𝑡}+𝑏)}$$
ここで、$${W}$$と$${b}$$は学習されたパラメータです。
デコーダの各時刻における出力$${st}$$の加重和を計算し、その結果をソフトマックス関数に通して次の単語の確率分布を得ています。ソフトマックス関数を使って、各次元の確率を計算し、合計$${1}$$になるように確率を揃えます。
このエンコーダ・デコーダモデルの仕組みは、特にAttentionメカニズムを導入することでさらに強力になります。Attentionメカニズムは、デコーダが入力シーケンスの特定の部分に焦点を当てて処理を行うことを可能にします。
さて、ここからはトランスフォーマーの話になるのでセクションを分けます!
大規模言語モデル(LLM)とTransformer
難易度⭐️|TransformerとAttntion機構
このセクションでは、これまで触れてきたような自己回帰モデルの課題を克服する、トランスフォーマー(transformer)とアテンション機構の説明です。
皆様が聞いたことがあるであろう、GPTもgenerative pretraining transformerの略であり、モデルの事前学習にトランスフォーマーを使っています。(とはいえ、GPTのアーキテクチャはエンコーダがないデコーダonlyです)
トランスフォーマーはシーケンスの各要素を逐次生成しますが、各生成ステップで全体のシーケンスを一度に考慮します。具体的には、queryとKey-Valueペアを用いて出力をマッピングする Scaled Dot-Product Attention(スケール化内積Attention)という仕組みを使っています。
各プロセスの詳細な解説の前にざっくり全体感を見て見ましょう。

ざっくり要約|transformerのエンコーダ
文章を入力行列(embedding行列)に変換した後、位置エンコーディング(入力埋め込みに位置情報を入れる)を追加し、一番下にあるEncoder(Encoder 1)に入力値として提供する。
Encoder 1は入力値を受け取り、Multi-head Attentionのサブレイヤーに値を送り、Attention行列を結果値として出力する。Multi-head Attentionは複数のアテンション機構を同時平行に実行する(RNNの課題克服!!)
Attention行列を次のサブレイヤーであるFeed-Forward Neural Networkに入力する。Attention行列を入力値として受け取り、残差接続とレイヤー正規化を経た後、Encoder表現を結果値として出力する。
Encoder 1の出力値をその上にあるEncoder 2に入力値として提供する。
Encoder 2は前と同じプロセスを行い、Encoder表現結果を出力として提供する。
以下を繰り返してデコーダに渡す。
ざっくり要約|transformerのデコーダ
Decoderに対する入力文をEmbedding行列に変換した後、位置エンコーディング情報を追加してDecoder(Decoder1)に入力。
Decoderは入力値を持ってきてMasked Multi-head Attentionレイヤーに送り、出力でAttention行列Mを出力。
Attention行列M、Encoding表現Rを入力してもらい、Multi-head Attentionレイヤー(Encoder-Decoder Attentionレイヤー)に値を入力し、出力で新しいAttention行列を生成。
Encoder-Decoder Attentionレイヤーから出力したAttention行列を次のサブレイヤーであるFeed Forward Neural Networkに入力する。Feed Forward Neural Networkではこの入力値を受け取り、Decoderの表現で値を出力。
次に、Decoder1の出力値を次のDecoder2の入力値として使用する。
Decoder2はDecoder1で行ったプロセスと同様に進め、ターゲット文に対するDecoder表現を出力。
DecoderはN個のDecoderを積むことができます。この時、最上位Decoderから得た出力(Decoder表現)はターゲット文章の表現になります。次に、ターゲット文章のDecoder表現をLinearおよびSoftmaxレイヤーに入力し、最後に予測された単語を得られます。

上の図のように、トークンごとにアテンションをFFNがブロックとして積み重なり、エンコーダとデコーダを作ります。
難易度⭐️|Positional Encoding
各単語の位置情報を埋め込むことで、モデルが単語の順序を理解できるようにする。(そのままだと、入力系列の順序情報を考慮できない。)
絶対位置符号化と相対位置符号化の2種類がある。絶対位置符号化は各単語の絶対的な位置を、相対位置符号化は単語間の相対的な位置関係を表現する。
トランスフォーマーに入力する前に単語の埋め込みに加えてやることがあります。それは、単語の位置情報の埋め込みです。
さて、アーキテクチャを再掲しますが、以下のPositional Encodingです。

Transformerブロック自身は単語の位置情報を把握できないので事前に埋め込む必要があり、周期的な挙動をするsin波cos波を加法します。
イメージは以下です。
$${WE("青の統計学")+PE("1番目のトークン")}$$
$${i}$$番目のトークンの位置情報の埋め込みは下のようになっております
$${\mathbf{p_i} = \begin{pmatrix} \sin\left(\frac{i}{10000^{\frac{2 \cdot 0}{d}}}\right) \\ \cos\left(\frac{i}{10000^{\frac{2 \cdot 0}{d}}}\right) \\ \sin\left(\frac{i}{10000^{\frac{2 \cdot 1}{d}}}\right) \\ \cos\left(\frac{i}{10000^{\frac{2 \cdot 1}{d}}}\right) \\ \vdots \\ \sin\left(\frac{i}{10000^{\frac{2 \cdot (d/2 - 1)}{d}}}\right) \\ \cos\left(\frac{i}{10000^{\frac{2 \cdot (d/2 - 1)}{d}}}\right) \\ \sin\left(\frac{i}{10000^{\frac{2 \cdot (d/2)}{d}}}\right) \\ \cos\left(\frac{i}{10000^{\frac{2 \cdot (d/2)}{d}}}\right) \end{pmatrix}}$$
$${i}$$は次元のインデックスです。
難易度⭐️⭐️⭐️ |Attention機構とTransformer
Attention機構は、入力系列の各要素に対して重要度を計算し、それに基づいて注意を割り当てる。
入力系列全体の情報(文脈情報)を考慮して各要素の重要度を計算する。
Transformerモデルでは、Self-Attention機構を多層に積み重ねることで、複雑な言語処理タスクに対応
では、数学的背景を見ていきましょう。
Attention機構の核心は、入力シーケンスの各要素に対して動的に重み付けを行い、出力の各ステップで最も関連性の高い情報に「注意を向ける」ことです。
Attentionの数学的表現は以下のようになります
$${Attention(Q, K, V) = softmax(\frac{QK^T}{\sqrt{d_k}})V}$$
$${Q}$$: クエリ行列
$${K}$$: キー行列
$${V}$$: 値行列
$${d_k}$$: キーの次元数
もうちょっと補足してみます。
Query(クエリ)
入力シーケンスの各トークンに対して生成されるベクトルです。クエリは、そのトークンが他のトークンに対してどの程度の注意を向けるべきかを表現します。つまり、クエリは「何に注目すべきか」という情報を提供します。
トランスフォーマーのコンテキストでは、クエリは一般的に入力系列の各要素に対応し、注意の対象となるトークンを示します。
数学的に表すと、クエリ$${Q}$$ は次のように表されます
$${Q=XW_Q}$$
ここで、$${X}$$ は入力(通常はエンコーダーの出力)、$${W_Q}$$はクエリ行列の重み行列です。
Key(キー)
各トークンに関連付けられたベクトルで、クエリとの関連性を計算するために使用されます。キーは入力系列$${X}$$の各要素に対応し、その要素がクエリとどの程度関連性があるかを示します。
数学的に表すと、キー $${K}$$ は次のように表されます
$${K=XW_K}$$
ここで、$${X}$$は入力(通常はエンコーダーの出力)、$${W_K}$$はキー行列の重み行列です。
Value(値)
値は、クエリに関連付けられる情報を持つベクトルを提供します。
通常、入力系列の各要素に対応し、その要素がクエリに対してどのような情報を持っているかを示します。
数学的に表すと、値 $${V}$$は次のように表されます
$${V=XW_V}$$
ここで、$${X}$$は入力(通常はエンコーダーの出力)、$${W_V}$$はvalue行列の重み行列です。
行列$${W_V,W_K,W_K}$$は、モデルの学習によって更新されるパラメータです。
Queryは探索対象、Key-Valueは探索の元データで、探索用途のKeyと本体のValueに分離することでより高い表現力を得ることができるということですね。
さて、式を再掲します。
$${Attention(Q, K, V) = softmax(\frac{QK^T}{\sqrt{d_k}})V}$$
この式は、クエリとキーの類似度を計算し($$QK^T$$)、その結果を正規化してから(softmax)、値に適用することで重み付けされた出力を生成します。
前述したように、Query、Key、Valueおよび出力は全てベクトルで、ソフトマックス関数の出力はValueベクトルの加重平均として計算されます。これにより、注意重みが計算され、各Valueベクトルの加重平均として最終的な出力が得られます
各Valueに割り当てられる重みは、Queryと対応するKeyの類似度から計算されます。
この類似度は、QueryベクトルとKeyベクトルの内積$${QK^T}$$をとることで得られます。
次に、類似度とvalueベクトルの積をとり、全ベクトルの総和を取ります。
これにより、アテンションの重みが計算され、各Valueベクトルの加重平均として最終的な出力が得られます。
Attentionの類似度に従って、valueベクトルの加重平均を算出します。これが第一トークンにおける、Attention機構の出力値になります。

*$${d_k}$$ はキーの次元数で、スケーリング因子として使用されます。このスケーリングは、大きな次元数における内積の値が非常に大きくなり、ソフトマックス関数が非常に急峻になることを防ぐためです。
もう少し専門的に言うと、内積をそのまま正規化するとQueryとKeyの次元数$${d_k}$$が大きくなるほどSoftmaxのlogitが飽和してしまう為、$${\sqrt{d_k}}$$で除算することで勾配消失を防ぎます。
ソフトマックス関数は、他のニューラルネットワークでも多く使われています。詳しくはこちらのコンテンツをご覧ください。
クエリ $${Q}$$、キー$${K}$$、バリュー $${V}$$ は入力シーケンスから線形変換によって得られ、各単語が他の単語に対して持つ重要度(注意重み)が計算されることがわかりました。これによって、Attention機構は、RNNの課題であった長距離依存関係の把握を克服し、より効率的で柔軟なモデルを実現できます。
トランスフォーマーのアーキテクチャーを見ると「Multihead Attention」と書かれています。
これは、異なる部分空間での先ほど説明した複数のセルフアテンションを並行して実行することで、モデルが異なる角度からの注意を学習できるようにするものです。具体的には、複数のヘッドでそれぞれ独自のクエリ、キー、バリューを計算し、それらを結合することで最終的な出力を得ます。
$${MultiHead(Q,K,V)=Concat(head_1,head_2,…,head_h)W^O}$$
ここで、各ヘッドは次のように計算されます:
$${head_𝑖=Attention(𝑄𝑊_𝑖^𝑄,𝐾𝑊_𝑖^𝐾,𝑉𝑊_𝑖^𝑉)}$$
$${W_i^Q}$$、$${W_i^K}$$、$${W_i^V}$$ はそれぞれのヘッドに対応する重み行列です。また、$${W^O}$$ は最終出力を得るための重み行列です。
この多頭注意機構により、モデルは異なる特徴を同時に学習(異なる部分空間で情報を捉える)できるため、より表現力豊かなモデルが構築されます。
トランスフォーマーは、セルフアテンション機構と多頭注意機構を組み合わせることで、シーケンス全体の文脈を効率的に捉えることができます。この仕組みによって、時系列に従ってトークンを取り込んでいたRNNでは実現しにくかった文脈理解を可能になっています。
ちなみに、このアーキテクチャがなぜtransformerと呼ばれるのかについてですが、attention is all you need と言う論文を拝見する限り
In this work, we presented the Transformer, the first sequence transduction model based entirely on attention, replacing the recurrent layers most commonly used in encorder-decorder architectures with multi-headed self-attention.
とあるので、RNNで見たリカレント層(繰り返し勾配を計算していたところ)を自己注意機構に置き換えたところから来ていると思います。
難易度⭐️|Feed Forward Network
Self-Attention機構で捉えられた文脈情報を、各位置ごとに独立に非線形変換する
隠れ層の次元を大きくすることで、モデルの表現力を向上させる(Transformerは多様なタスクに対応するため)
Self-Attention機構と並んで、Transformerブロックの基本的な構成要素
さて、アーキテクチャを再掲します。

トランスフォーマーモデルの各レイヤーにおいて、自己注意機構の後には位置ごとに独立した全結合のフィードフォワードネットワークが適用されます。このネットワークは、各トークンの表現を非線形変換する役割を担います。
ざっくりといえば、巨大な二階建てのMLP(多層パーセプトロン)です。多層パーセプトロン。先ほど扱いましたが、覚えておりますか?
各位置のatttention行列から得られるトークン表現に対して同一の変換が適用され、出力されます。具体的には以下のように計算されます
$${FFN(x)=max(0,xW_1+b_1)W_2+b_2}$$
お馴染みのRelu関数を使っています。
負の数だと0を返し、それ以外だとそのまま入力値を返す活性化関数でした。
$${W,b}$$はそれぞれ重みとバイアスで、学習パラメータになります。
「なんでパラメータがReluの外についているの?」
と気になった方、いい質問です。
端的に言うと、次元を増やしてその後戻しています。

入力ベクトルに対して最初の線形変換(中間層のReluを通しただけ)を行うことで、次元が拡張されます。非線形活性化の後、次にもう一つの線形変換を行い、元の次元数に戻します。
大体ですが、中間層の次元は入力出力の次元の4倍ほどと呼ばれています。
今は昔のGPT-3の場合だと
入力層/出力層の次元数:12,288
中間層の次元数:12288×4= 49,152
総ブロック数:96
Feed Forwardのパラメータ数:12288×49152×2×96≒116B
GPT-3の総パラメータ数:175B
なので、Feed Forwardが全体に占めるパラメータの割合:約66%です。
LLMの大規模さを象徴するのは、実はFFNの部分なのです。
FFNは、Attention行列のKeyvalueで蓄積した知識を抽出する機構といわれております。トークンごとの表現を個別に処理するため、自己注意機構で得られた文脈情報をさらに抽出・変換する役割を果たします。この非線形変換により、モデルはより複雑な関係を学習しやすくなります。
自己注意機構の後に適用されるため、各トークンの文脈情報を考慮した上で、各トークンの特徴を深く掘り下げることができるということですね。
→入力シーケンス全体の複雑なパターンをより良く捉えることができる。
難易度⭐️|残差接続とレイヤー正規化
残差接続:勾配を層を飛び越えて伝播させることで、深いネットワークでも勾配消失や勾配爆発問題を緩和し、学習を安定化させる。
レイヤー正規化:各層の入力を正規化することで、学習中の活性化関数の飽和を防ぎ、勾配消失を抑制する。
具体的には、正規化により層間の共変量シフトを軽減し、モデルがより汎化性能の高い表現を学習できるようになる
どちらもTransformerモデルの成功に不可欠な要素
さて、FFNの後です。
アーキテクチャを再活しますが、「Add&Norm」の部分ですね。

トランスフォーマーモデルでは、FFNの各層に対して残差接続と正規化(Layer Normalization)が施されています。これにより、勾配消失問題を緩和し、学習の安定性と速度を向上させています。
残差接続は以下のように行われます
$${FFN_output=LayerNorm(X+FFN(X))}$$
$${\text{FFN}(X)}$$はFFNの出力
$${X}$$は自己注意機構の出力
$${\text{LayerNorm}}$$はレイヤー正規化で、隠れ層の次元軸で平均と分散をとり正規化しています。
このように、入力をそのまま出力に加えることで、情報の伝播を助けています。
テキスト系の入力だと、シーケンスの長さがサンプルごとに違うのがあたりまえですよね。なので、バッチ正規化ではなくレイヤー方向での正規化を行うのが基本です。
Transformer|デコード方式と生成プロセスの外観
いよいよ出力の部分になります。
先ほどテキスト生成タスクではモデルは、次の単語の生起確率を出力すると言いましたが、実は事前学習済みLLMを使って, テキストを出力(デコード)するにあたり、デコード方式がさまざまあるのです。
Greedy Decoding
これは一番想像がしやすいと思います。
各ステップで最も確率の高いトークンを選択するシンプルなデコード方式です。この方法は計算効率が高く、実装が簡単ですが、必ずしも最適な文生成にはならないことがあります。
つまり、次のトークン$${y_t}$$は以下のように決定されます。
$${y_t=argmax_y(y|y_1,y_2,y_{t-1})}$$
「東京」に続く生起確率が高いトークンが「都」だとしても、「駅」だったり「に、を。。」みたいな助詞が来るかもしれませんよね。最適解を見逃す可能性が高い(局所最適解に陥りやすい)と言うのが、greedy decodingの欠点です。
Beam Search
Beam SearchはGreedy Decodingの改良版で、複数の候補シーケンスを追跡し、最も有望なものを選択する方法です。この方法は、局所最適解を避け、より良い全体的な解を見つけるために使用されます。
以下は手順になります。
初期トークンから開始し、ビーム幅(シーケンス集合)$${B}$$を設定。
モデルに現在のシーケンスを入力し、次のトークンの確率分布を取得。
各シーケンスについて、次の$${B}$$個の最も確率の高いトークンを選択し、新しい部分シーケンスを生成します。$
各新しいシーケンスのスコア$${S}$$を計算し、上位$${B}$$個のシーケンスを保持。$${S(\mathbf{y})=logP(\mathbf{y})}$$
終了トークンが生成されるか、最大長に達するまでステップ2-4を繰り返す。
最終的にスコアの最も高いシーケンスを選択。
ビーム幅というハイパラを次第では、計算量が非常に大きくなってしまいますが、ある程度シーケンスの大きさを確保して確率が最大となるものを考えるので、より多様で質の高いシーケンスを生成できるし、局所解に陥りにくいです。
まあ毎回最大のものを取らずに、いくつか候補を取っておくので計算量は多くなります。

上の図でデコーダ方法の違いを視覚的に理解しましょう。
Greedy Searchは各ステップで最も高い確率のパスのみを選択し、Beam Searchは複数のパスを同時に追跡して最も有望なパスを選びます。
これに限らず、貪欲法は計算量が少なくすみますが、局所解に陥理やすいという特徴があるのです。
さて上記の通り方式は違えど、デコーダーは各ステップで次の単語の確率分布を予測します。
この確率分布 $${P(y_t∣y_1,y_2,…,y_{t−1})}$$は、現在のシーケンスが与えられたときに次に来る単語の確率を示します。ここで重要なのは、この予測確率分布が実際の分布にどれだけ近いかという点です。
つまり、生成される文章が自然で正しいものになるためには、学習過程で予測分布と実際の分布との差を最小限に抑える必要があります。
さて、予測分布と実際の分布との差を測るために、クロスエントロピー(cross-entropy)を使用します。クロスエントロピーは、2つの確率分布間の違いを測定するための標準的な手法です。
損失(loss function)は次のように定義されます。
$${\mathbf{L}=-\frac{1}{N}\sum_{i=1}^N\sum_{t=1}^{T_i}y_ilog(\hat{y_{i,t}})}$$
$${y}$$ :実際の分布
$${\hat{y}}$$ :予測分布
$${N}$$ :バッチサイズ
$${T_{i}}$$ はシーケンス$${i}$$の長さ
この損失関数を最小化するために、Adamオプティマイザーを使用してモデルのパラメータを更新します。(Adamは前のセクションで扱いました。覚えていますかね?)
補足|クロスエントロピーとKLダイバージェンスについて
分布間の距離と聞いて、KLdivergenceが浮かんだ方はよく勉強していると思います。クロスエントロピーとの関係を見て見ましょう。
繰り返しになりますが、クロスエントロピー $${H(p,q)}$$ は、実際の分布 $${p}$$ と予測分布 $${q}$$ の間の平均的な不確実性を測る尺度です。
$${H(p,q)=-\sum_{x}p(x)log q(x)}$$
ここで、 $${p(x)}$$ は実際の分布、$${q(x)}$$ は予測分布です。
一方、KLダイバージェンス $${D_{KL}(p||q)}$$ は、分布 $${q}$$ が分布 $${p}$$ からどれだけ逸脱しているかを測る尺度です。
$${D_{KL}(p||q)=\sum_{x}p(x)log\frac{p(x)}{q(x)}}$$
クロスエントロピーとKLダイバージェンスの関係は次のように表されます。
$${𝐻(𝑝,𝑞)=𝐻(𝑝)+𝐷_{KL}(p||𝑞)H(p,q)=H(p)+D_{KL}(p||q)}$$
これにより、クロスエントロピー $${H(p,q)}$$はKLダイバージェンス $${D_{KL}(p||q)}$$ と分布 $${p}$$ のエントロピー $${H(p)}$$ の和であることがわかります。
エントロピー $${H(p)}$$ は定数であり、予測分布 $${q}$$ には依存しません。したがって、クロスエントロピーを最小化することは、KLダイバージェンスを最小化することと同等です。
KLダイバージェンスに関するこちらの記事も参考になると思います。
生成AIへのtransformer活用|ダンス生成AIを例に
さて、ここまでトランスフォーマーの仕組みを深掘りしてきましたが、このプロセスを経て、生成タスクができていることを実感するために、ダンス動画生成モデルの論文をちょこっと紹介します。
皆さんは、tiktokやinstagramでアニメキャラクターや著名人が踊っているAI動画を見たことがありますか?
2023年初めくらいは、顔の動きや手足の挙動が現実離れしており、見るも耐えない動画でしたが、技術の進歩は凄まじく、今ではそのままアニメにできそうなくらい素敵な動画が生成されていますね。

こうした動画生成モデルの仕組みが、これまで学習したtransformerの仕組みを使っています。詳しく見ていきましょう。今回は以下の論文を解説いたします。
この論文のモデルのモチベーションは、音楽特徴と既存のダンスポーズシーケンスを基に、将来のダンスポーズを予測し、最終的にダンス動画を生成することです。音楽と、途中までのダンスで最終的にその後のダンスがどうなりそうかを考えてくれます。
入力データ
モデルに与えられる入力データは、音楽特徴とダンスポーズシーケンスです。何よりまずベクトルに変換しないと始まらないので、なんとかして特徴量をベクトルに変換します。
音楽特徴 (M): 時系列音楽データを抽出し、適切な次元に埋め込みます。
ダンスポーズシーケンス (P): 各ポーズを関節位置や角度などの特徴に変換し、時系列データとして扱います。
$${M,P}$$の抽出が個人的に一番興味深いです。
入力データ|音楽データ
まず、音楽データから特徴を抽出します。この際に、Librosaのような音響処理ライブラリを使用して、以下のような特徴を抽出します。
メル周波数ケプストラム係数 (MFCC):人間の聴覚特性に基づいて音声信号を表現します。
MFCCデルタ:MFCCの時間的な変化を捉える特徴です。
定常Qクロマグラム:音楽の調性やコード進行を表現します。
テンポグラム:音楽のテンポを捉える特徴です。
オンセット強度:音の始まりの強さを表現します。
抽出した音楽特徴を適切な次元に整形し、ニューラルネットワークに入力できる形式に変換します。
入力データ|ダンスポーズシーケンス
①ポーズデータの収集と整形:3Dポーズデータ(例えば、各フレームの関節の位置や角度)を収集し、関節位置の配列として整形します。これには通常、モーションキャプチャデータが用いられます
②上半身と下半身の分割:ポーズデータを上半身と下半身に分割し、それぞれを独立した特徴ベクトルに変換します。上半身と下半身の動きを別々にモデル化するってことですね。これにより、ポーズの組み合わせの多様性を確保します。
→ただし、このままだと上半身と下半身が通常ありえない形で接続されてしまう恐れがあるので上半身、下半身の特徴間の因果関係を保持しつつ、異なるコンポーネント間で情報を交換するためにアテンション機構が設計されています。めっちゃ興味深いです。
今回の入力データは、「今このビートが流れているから、こうやって上半身は動かして、それに合わせて下半身はリズムをとる」みたいに、特徴量間の因果関係がしっかりあるのが特徴です。
ダンスのポーズコードシーケンスの長さ$${T'}$$に対して、上半身と下半身のポーズコードを学習可能な特徴$${u}$$と$${l}$$に埋め込みます。
音楽的特徴とダンスシーケンスの埋め込みができました。
ダンスシーケンスを時間軸で音楽特徴と連結し、学習された位置埋め込みを追加して、連結された$${(3×T')×C}$$テンソルを12個の連続するトランスフォーマーレイヤーに渡します。
アテンションの適用と出力
埋め込まれたベクトルをクエリ $${Q}$$、キー $${K}$$、バリュー $${V}$$ に分割します。
$${Q=W_p\cdot M_{embed}}$$
$${K=W_k\cdot P_{embed}}$$
$${V=W_v\cdot P_{embed}}$$
ここで、 $${W_q}$$,$${W_k}$$, $${W_v}$$ はそれぞれクエリ、キー、バリューに変換するための重み行列です。
次に、クエリとキーの内積を計算し、スケールした後にソフトマックス関数を適用してアテンションスコアを求めます。$${d_k}$$はキーの次元数でしたね。
$${scores=\frac{Q\cdot K^T+M}{\sqrt{d_k}}}$$
$${Attention=softmax(scores)}$$
ちょっと見慣れない$${\mathbf{M}}$$が出ました。
これはマスク行列$${\mathbf{M}}$$です。3×3のブロック行列であり、下三角行列のサイズ$${T'}$$を要素とします。この設計により、異なるコンポーネント間の情報交換が可能になり、将来の情報が過去に伝達されないことが保証されます。
補足|ソフトマックス関数と負の値
ここは汎用的なテクニックなので少しまとめます。
上で、マスク行列$${M}$$を追加しましたが、それによりなぜ未来の情報が過去の情報に影響を与えないことが保証されるのでしょうか?
$${M = \begin{bmatrix} M_{mm} & -\infty & -\infty \\ M_{um} & M_{uu} & -\infty \\ M_{lm} & M_{lu} & M_{ll} \end{bmatrix} }$$
因果アテンション層では、音楽特徴($${\mathbf{m}}$$)、上半身のポーズコード($${\mathbf{u}}$$)、下半身のポーズコード($${\mathbf{l}}$$)の間で情報を交換しながら、上のような下三角マスクを使用します。
$${M_{mm}}$$: 音楽特徴の自己アテンション(未来の情報を参照しない)。
$${M_{uu}}$$: 上半身ポーズコードの自己アテンション(未来の情報を参照しない)。
$${M_{ll}}$$: 下半身ポーズコードの自己アテンション(未来の情報を参照しない)。
$${M_{um}}$$: 音楽特徴から上半身ポーズコードへのアテンション(音楽特徴が現在と過去のみを参照)。
$${M_{lm}}$$: 音楽特徴から下半身ポーズコードへのアテンション(音楽特徴が現在と過去のみを参照)。
$${M_{lu}}$$: 上半身ポーズコードから下半身ポーズコードへのアテンション(上半身が現在と過去のみを参照)。
このマスク行列により、スコアが計算されていましたね。
$${scores=\frac{Q\cdot K^T+M}{\sqrt{d_k}}}$$
右半分が大きい負の値(通常は $${-\infty}$$)になることで、その位置のソフトマックス関数が実質的にゼロになるため、これらの値は無視されます。これにより、未来の情報が現在および過去の情報に影響を与えることを防ぎます。
ソフトマックス関数の特徴を思い出すと、
$${softmax(x)=\frac{e^{x_i}}{\sum_{j}e^{x_j}}}$$
入力された値の相対的な重要性を計算し、確率として出力しましたね。スコア行列の右半分に大きい負の値($${-\infty}$$)を設定することで、その要素は無視され、実質的にゼロとして扱われます。
高校数学で習いましたが、$${-\infty}$$に対する指数関数はゼロになりましたよね。
さて、アテンションスコアとバリューを掛け合わせて、最終的なコンテキストベクトルを得ます。
$${Context=Attention⋅V}$$
得られたコンテキストベクトルをTransformer層に入力し、次のポーズシーケンスを予測します。
$${𝑃_{next}=Transformer(Context)}$$
最終的に、出力されたポーズシーケンスはデコードされ、具体的な関節位置や角度としてダンス動画に変換されます。
最後に
お疲れ様でした!
ここまでかなり時間がかかったかと思います。
ビジネスでデータサイエンスを使うモチベーションや、生成AIの裏側の構造などをしっかりと理解できたと思います。
青の統計学は公式LINEもやっております!
最新記事のお知らせや新サービスの広報、限定コンテンツの投稿などを準備しております。ぜひご登録ください(全然うるさくないですよ❤️)
おまけ|ビジネスにデータサイエンスを使う気ならこれを読んでほしい
毎回noteの最後に良書を紹介していますが、今回はデータサイエンスの方法論はちょっと離れます。が、めちゃくちゃ大事です。
イシューから始めよーー知的生産の「シンプルな本質」
商品概要と感想
イシューを分解してドライバーを探す作業として全体構成と因数、打ち手を探す
大きな問いを細分化していく、解答できる問いを定義していく
などなど、具体的な話というよりはやや抽象度が高い概念先行で論を進めて、問題設定&解決法について語っています。
この本では、上で話した「ビジネスにデータサイエンスを使うということ」をもっと抽象化してちゃんと書かれています笑
一貫して平易な表現がなされていることが特徴的で、誰にでも理解しやすく、ただ身につけて自分の力とするのは何年もかかりそうな本です。
また次回の記事でお会いしましょう。
こちらの記事もよろしくお願いいたします。
この記事が参加している募集
頂いた活動費は、全て「青の統計学」活動費用に使います!note限らずサービス展開していくのでお楽しみに!
