
斜方投射シミュレーターを作ってみる。#1【物理】
最近X(旧Twitter)とアカウント連携した、"とりすてぃっく"です。
いつぞやの記事にて、斜方投射について扱ったんですが、
これをもっと分かりやすくしたいなと思って、
シミュレーターを作ることにしました。
たぶん物理を勉強している人たちにとっても
有益なものになると思います。
あと、雪合戦が好きな子どもたちにも…
ぜひ、参考にしていってね。
そもそも斜方投射ってなに?
ここでは斜方投射について詳しく知らない人に向けて
解説していきます。
ざっくり言うと、
斜方投射とは、ハンドボール投げみたいなものです。
たぶん、"能登殿の最後について。【物理】"を見れば、
大体どんなものかはわかるとおもいます。
斜方投射について考えるときは、
そのまま考えるのはとても大変なので、
鉛直方向(縦方向)と、水平方向(横方向)に分けて
考えていくのが基本です。
とりあえずは空気抵抗ないやつを考えていこう。


縦方向は、ボールを真上に投げるだけの運動で、
横方向は、まっすぐに前に進んでいくだけの運動です。
それぞれを考えてから、この2つを組み合わせれば
斜方投射の運動になります。
まずは、水平方向を考える。
まずは、簡単そうな横方向の動きを見ていきましょう。
この横方向の運動は、等速直線運動と呼ばれるもので、
ずーっと同じ速さで直線的に動くよってやつです。
そのため、計算はとっても簡単!
ただ、(速さ)x(時間)=(距離)ってやつだけで
いいんですよ。いわゆる、"きはじ"ってやつね。
物理学の世界では、これを文字に置き換えます。
$$
x = vt
$$
vは、velocity(速さ)のことで、tは、time(時間)のこと。
xは、水平方向の距離のことです。x軸方向だから、xなんです。
ここの速さは、時間がたっても変化しないので、
一番最初の速さ(初速度)と時間経過したときの速さは同じです。
初速度を$${v_{0x}}$$とおくと、
$$
x = v_{0x}t
$$
これで、水平方向の距離について求めることができました。
次に、鉛直方向を考える。
次に、縦方向の動きについて考えていきます。
この縦方向の運動は、鉛直投げ上げ運動と呼ばれるやつです。
ただ、これはだんだんボールの速度が遅くなっていって、
最終的には、地面に落下していくような運動なので
ちょっとだけ面倒です。
そのため、まずは速度について調べていきます。
まずは初速度を$${v_{0y}}$$とおきます。
速度は、重力によってどんどん遅くなっていきます。
ここで使う値は、重力加速度というやつです。
加速度とは、時間経過によってどれだけ速度が変化するのかを
示す値で、例えば車が$${10 \scriptsize km/h}$$で走っているとき、
加速度が$${10 \scriptsize km/h^2}$$だったら、1時間後(1h後)には、
$$
10 {\scriptsize km/h} +10{\scriptsize km/h^2} \times 1{\scriptsize h} = 20{\scriptsize km/h}
$$
このように、$${20{\scriptsize km/h}}$$となることが分かります。
つまり、加速度の単位である$${km/h^2}$$は、1時間後には、
なんとか$${km/h}$$だけ速度が変化するということを表しています。
もし、$${m/s^2}$$だったら、1秒後(1s後)には、なんとか$${m/s}$$だけ
速度が変化するということになります。
そして、重力加速度はだいたい、$${g = 9.8 \scriptsize m/s^2}$$の値を持つ加速度で、
これが上に投げ上げられた物体にかかるので、
$${t \scriptsize [s]}$$後の物体の速度は、$${gt \scriptsize [m/s]}$$だけ
遅くなるということになります。
よって、上に投げられた物体の$${t \scriptsize [s]}$$後の速度$${v_{y} \scriptsize [m/s]}$$は、
$$
v_{y} = v_{0y} - gt
$$
となります。
初速度を$${98 \scriptsize m/s}$$として、これをグラフで表すと、

こんな感じになります。段々と速度が落ちていくのが分かりますね。
ここから鉛直方向の距離を求めていこうと思います。
距離は、水平方向のときと同じく、(速さ)×(時間)で出せるんですが、
速さが変化してしまうので、このままでは難しい。
そこで、面積を使っていきます。
先ほどのグラフとx軸で囲まれた部分が距離になるんです。
そのため、積分を使えば、(積分定数をCとする。)
$$
\begin{array}{} y &=& \int v_{0y}-gt dt \\\
&=& v_{0y}t- \frac{1}{2}gt^2 + C \end{array} \\
\\
初期位置を0 {\scriptsize m}とすると、\\
\\
y = v_{0y}t - \frac{1}{2}gt^2
$$
こんな感じで出せますが、積分を使わない場合は、

グラフの面積を求めていきます。
これは、以下のように分けられるので、
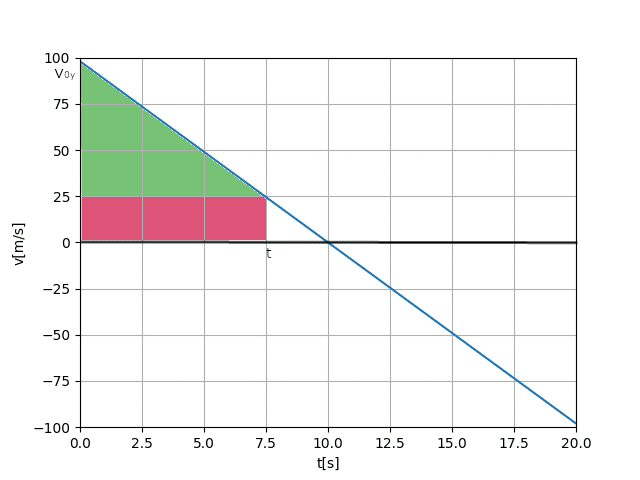
緑と赤の面積をそれぞれ求めると、
$${t \scriptsize [s]}$$のときの速度$${v_{y}}$$は、
$${v_{y} = v_{0y} - gt}$$なので、
$$
(1)緑色の部分の面積S_{1} \\
\begin{array}{}S_{1} &=& t \times (v_{0y}-(v_{0y}-gt)) \times \frac{1}{2} \\\
&=& \frac{1}{2}gt^2\end{array} \\
\\
(2)赤色の部分の面積S_{2} \\
\begin{array}{}S_{2} &=& t \times (v_{0y}-gt)\\\
&=& v_{0y}t-gt^2\end{array} \\
\\
(3)全体の面積S \\
\begin{array}{}S &=& S_{1}+S_{2}\\\
&=& \frac{1}{2}gt^2+v_{0y}t-gt^2\\\
&=& v_{0y}t - \frac{1}{2}gt^2\end{array}
$$
こんな感じで出すことができます。
したがって、面積=距離なので、
$$
y = v_{0y}t - \frac{1}{2}gt^2
$$
このように出せました。
連立して関数グラフを作る。
ここでは、先ほど導出した、2つの式を連立して
関数グラフを作っていきます。
$$
\begin{cases} x = v_{0x}t \\\
y = v_{0y}t - \frac{1}{2}gt^2 \end{cases}
$$
ちょっとその前に、2つの式の初速度について考えていきます。
そもそも、ボールはこのように斜めの初速度を持って
投げ出されています。

これを分解すると、

こんな風になります。なので、三角比を使うと、
$$
v_{0x} = v_{0}\cos \theta \\
v_{0y} = v_{0}\sin \theta
$$
このように表せます。したがって、
$$
\begin{cases} x = v_{0}\cos \theta \times t \\\
y = v_{0}\sin \theta \times t - \frac{1}{2}gt^2 \end{cases}
$$
このようになり、ここからtを消去すると、
$$
y = \tan \theta \times x - \frac{g}{2v_{0}^2 \cos ^2 \theta} \times x^2
$$
軌道の式が出せました。
これを描画すると、斜方投射の様子が分かります。
しかし、残念ながら今回はここまでです。記事が長すぎた…
一応ここまでのお話をまとめると、
$$
v_{0x} = v_{0}\cos \theta \\
v_{0y} = v_{0}\sin \theta \\
\begin{cases} x = v_{0}\cos \theta \times t \\\
y = v_{0}\sin \theta \times t - \frac{1}{2}gt^2 \end{cases} \\
y = \tan \theta \times x - \frac{g}{2v_{0}^2 \cos ^2 \theta} \times x^2
$$
こんな感じです。
次回予告
次回は、今回出した軌道の式を用いて
シミュレーターを作っていきます。
ついでに空気抵抗まで考えちゃいます。
果たして"とりすてぃっく"の体力は持つのか…?
次回、シミュレーター制作編、乞うご期待!
