正多角形の外周と円周率について。【数学】

どうも、”とりすてぃっく”です。

今回は正多角形の面積から
円の面積の近似をしていこうと思います。

ちなみに、今回の記事は
三角比の話がほんの少しだけ分かれば
理解できると思います。

あと、ちょっとした試みで、
最後のおまけPartだけ、
有料記事にしてみました。

↓前回の円周率の記事はこちらからどうぞ。

内接と外接

今回円周率の近似をするにあたって、
円に外接する正多角形の外周と
内接する正多角形の外周を
求めていくんですが、

そもそも、内接と外接とは何かというと、
図で表すとこんな感じです。

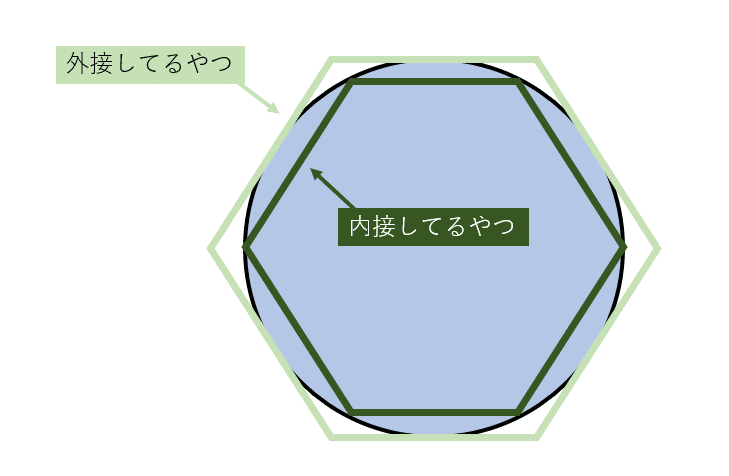
内接している正多角形の外周は、
円周よりも少し短くなってしまう。

外接している正多角形の外周は、
円周よりも少し長くなってしまう。

じゃあ、2つの平均を考えれば
いいのではないでしょうか。

というわけで、
両方とも求めていきます。

内接している正多角形

今回は、試しに正六角形の外周を
求めてみましょう。

こちらの求め方は、

1. 正多角形の頂点と中心を結んで
   三角形を作る。

2. 余弦定理を使って三角形の
   円に近い方の長さを求める。

3. 求めた長さを使って
   多角形の外周の長さを求める。

この手順でいきます。

外周(赤い部分)を求めたい

円の半径を1とすると、三角形は、

この図のようになります。

今回は正三角形になるので、
余弦定理を使う必要はありませんが、
これを使って求めると、

$$
\sqrt{1^2 + 1^2 - 2 \cdot 1 \cdot 1 \cdot \cos 60^{\circ}} = 1
$$

このようになります。

ちなみに、余弦定理は、

直角三角形じゃなくてもいい。

こんな三角形があるとき、

$$
c^2 = a^2 + b^2 - 2ab \cos \theta
$$

が成り立つというやつです。

今回は三角形が6つあるので、外周は、

$$
1 \times 6 = 6
$$

6となります。

外接している多角形

こちらの求め方は、

1. 正多角形の頂点と中心を結んで
   三角形を作る。

2. $${\tan \theta}$$を使って三角形の
   円に接している辺の長さを求める。

3. 求めた長さを使って外周を求める。

この手順でいきます。

円の半径は1としているので、三角形は、

この図のようになります。

赤い部分は$${\tan \theta}$$を使うと、

$$
1 \times \tan 30^{\circ} \times 2 = \frac{2\sqrt{3}}{3}
$$

このように求められます。

なので、正多角形の外周は、

$$
\frac{2\sqrt{3}}{3} \times 6 = 4 \sqrt{3}
$$

$${4 \sqrt{3}}$$と求められます。

大体の円周率

内接している方と外接している方の
両方が求められました。

ということで、円周率は、
円周が、$${2 \pi}$$なので、

$$
6 < 2 \pi < 4 \sqrt{3} \\
3 < \pi < 2 \sqrt{3}
$$

このようになります。

$${3}$$と$${2 \sqrt{3}}$$の平均は、
3.23205…となりました。

やはり、正六角形では精度が悪いですね。

正八角形や正十二角形など、
頂点の数を増やしてみると
もっと正確な値が出せるはずです。

正n角形と極限(おまけPart）

ここからは、正n角形と極限を使って
円周率を求めていきます。

• 本当に正n角形のnを大きくし続けたら
  円周率が出せるのか?

• 導出した式を使って
  円周率を求めるプログラムを作った話

こんなものがあります。