人の都市間移動の統計的法則性(重力モデルから放射モデルへ)【統計力学の不思議世界探索】#32
人口の多い都市と少ない都市が近くにあったとして、その両都市からちょうど等距離あたりに住んでいる人は、買い物や職探しでどちらの都市に行くことが多いだろうか?

(GoogleMapより一部加筆)
行く頻度としては人口の多い都市によく行くと多くの人は思うだろう。どういう店や会社があるかなど、要因は一人ひとりちょっとずつ異なるのであまり考えないことにするが、統計的に考えたときに何らかの法則性は見出せないだろうか。
そのモデルとして、都市の人口が多いと重力が働くように周囲の人を引きつけるようになると考えて定式化されたのが重力モデルである。上に挙げたような等距離に人口の多い都市と少ない都市がある例では、人口の多い都市からのほうが強い"引力"(あくまでイメージなので" "を付ける)が働いてそちらに流れる人が多くなるという考えである。式で書くと次の通り。
$${T_{ij}=\frac{m_i^αn_j^β}{f(r_{ij})}}$$(1)
$${T_{ij}}$$は都市 i から都市 j への人の流れ、$${m_i, n_j}$$はそれぞれ都市 i, j の人口、α, βは任意の指数、$${r_{ij}}$$は都市 i, j 間の距離で、$${f()}$$は何らかの関数。
これはニュートンの万有引力の法則$${F=G\frac{Mm}{r^2}}$$に似ているがちょっと拡張したものになっている。$${α=1, β=1, f(r)=\frac{1}{G}r^2}$$ならば全く同じになるが、$${α, β}$$は1でない指数も取りうるし、距離$${r}$$についても2乗とは限らない。このおかげで、現実の様々な都市にも柔軟に対応できる。
直観的にもわかりやすくて良さげに見える重力モデルだが、1946年に提唱されて以降数多くの検証に晒され、今ではいくつもの問題点が指摘されている。
(i) 理論的導出が不明
(ii) 現実の都市と合致する$${α, β, f()}$$を決めるのに最大9種類も統計量が必要
(iii) 過去のデータから$${α, β, f()}$$を合致させても、パンデミックのような新奇な現象には合致するとは限らない
(iv) 似た地域で同じ$${α, β, f()}$$を当てはめても桁違いにずれることがある
(v) 都市の人口が増えると引きつける人口も増えることになるが、後背地の人口は有限なため頭打ちになるという制限が含まれておらず、無制限に人口が増えるという乖離も起こる
(vi) 決定論的モデルであり、移住者の流動は予測できない
これらの問題点を一挙に改善する新しいモデルが、今回紹介する論文で2011年に提唱された放射モデルだ。
(なんか偏ってないかと思われるかもしれませんが、私の興味でまたも都市の話です!)
統計力学の不思議世界探索、今回紹介する論文はこちら。
A universal model for mobility and migration patterns
移動と移住パターンの普遍的モデル
https://arxiv.org/pdf/1111.0586
本論文では、主にアメリカの群(county)を基本単位として統計的な解析を行う。日本では、町村くらいでしか群は意識されないが、いくつかの市区町村をまとめた区分で、州より1段小さく、市区町村より1段大きい区分。
人口数千から数百万まで桁が3つや4つも違う都市とは違い、群は比較的均等にアメリカ全体を分割しているとされ(ニューヨーク市などの大きな市は複数の群に跨ることもある)、アメリカの国勢調査は群を基本単位としている。
本論文が提唱する放射モデルは、次のように考える。都市間の通勤の流れがどのように作られるかというと、職探しの時の諸条件によって決められるので、ある群に住んでいる人が職探しをするとき、次のように決めるとする。
(1) アメリカ全土から求人を探すとし、各群での求人の数はその群の人口 n に比例するとする。各群には$${n_{jobs}}$$件の求人があり、その職に就くことの利益 z は、給料、労働時間、通勤距離、その他就労条件などの組み合わせを表す分布p(z)からランダムに選ばれるとする。この分布p(z)はたくさんの求人を見て利益 z のヒストグラムを取ったものとほぼ一致するだろう。人口 n を持つ各郡には、分布p(z)に従う$${\frac{n}{n_{jobs}}}$$個のランダムな数$${z1, z2, …, z_{\frac{n}{n_{jobs}}}}$$が利益として提示され、郡の人口が大きいほど、より多くの雇用機会を提供することを考慮している。
(2) 単に給料が高いのではなく給料、労働時間、通勤距離、その他就労条件などを組み合わせた総合的な利益 z が最も高い仕事を選ぶとする。通勤距離が考慮されることによって、家から近いところから順に見ていって良い仕事があればそこに決めるということになる。

Saragota群(青)の人が職探しをするとき、近くから探していき(黄色の範囲)、その中で出身群より良い仕事があるうち一番近いところ(ここではOneida群(緑))に仕事を決める
ここで、本論文後半の付録2章の放射と吸収の一般法則をさらっておく。
太陽内部の放射層(?!)が典型的であるが、有限温度で黒体放射する一般の原子の集団の中で、あるところから光子が放射されて別のところで吸収されるのがあちこちで繰り返される様子を統計的に記述する法則である。
原子集団の中の場所 i から放射される光子の数を$${z^{(i)}}$$とする。原子集団の中での温度や密度のムラによって$${z^{(i)}}$$が大きい放射優勢の場所と$${z^{(i)}}$$が小さい吸収優勢の場所は発生する。
場所 i の密度$${m_i}$$について、ある確率分布$${p(z)}$$から乱数を$${m_i}$$回とったうちの最大値として$${z^{(i)}}$$は決まるとする。なので、原子の密度が高い場所ほど放射優勢となる。(分布$${p(z)}$$は温度によって変わるが、ここではあまり考えない。)
場所 i から放射された光子は、その周りで$${z^{(j)}}$$が吸収閾値を下回るある場所 j で吸収される。場所 j の密度を$${n_j}$$とし、場所 i から j までの距離を r として場所 i から半径 r の範囲の粒子数を$${s_{ij}}$$とする。場所 i から放射された光子は、できるだけ近いところで吸収してくれるところを探して場所 j を見つけ出して吸収されるというイメージ。そうして、場所 i から場所 j への放射が起こる確率$${P(1|m_i, n_j, s_{ij})}$$は次のように書ける。
$${P(1|m_i, n_j, s_{ij})=\int_0^∞P_{m_i}(z)P_{n_j}(> z)P_{s_{ij}}(< z)dz}$$
$${P_{m_i}(z)}$$は、確率分布$${p(z)}$$から乱数を$${m_i}$$回とったうちの最大値がzになる確率であり、次のように書ける。
$${P_{m_i}(z)=\frac{dP_{m_i}(< z)}{dz}=m_ip(< z)^{m_i-1}\frac{dP(< z)}{dz}}$$
同様に、
$${P_{s_{ij}}(> z)=p(> z)^{s_{ij}}}$$
$${P_{n_i}(< z)=1-p(> z)^{n_i}}$$よって、
$${P(1|m_i, n_j, s_{ij})=m_i\int_0^∞\frac{dp(<z)}{dz}[p(<z)^{m_i+s_{ij}-1}-p(<z)^{m_i+n_j+s_{ij}-1}]dz}$$
$${ =m_i[\frac{1}{m_i+s_{ij}}-[\frac{1}{m_i+n_j+s_{ij}}]}$$
$${ =\frac{m_in_j}{(m_i+s_{ij})(m_i+n_j+s_{ij})}}$$ (S2)
気付いたかもしれないが式(S2)の放射吸収の一般法則の導出は、その前の段落で説明した、人の職探しの規則と酷似している。式(S2)は一般の原子集団における光子の放射吸収であるため、都市間の人の移動にもそのまま当てはめることができる。(酷似しているがあくまで類推であり、どれほど妥当かは要検証であるが)
場所 i から j への通勤の流れ$${T_{ij}}$$は、出発地の群の人口$${m_i}$$と目的地の群の人口$${n_j}$$と、出発地から目的地までの距離を半径とする円内(求職時に探した範囲)の人口$${s_{ij}}$$を用いて
$${T_{ij}=T_i\frac{m_in_j}{(m_i+s_{ij})(m_i+n_j+s_{ij})}}$$(2)
と書ける。$${T_i}$$は場所 i を出発地とする人の数。
これは、冒頭に挙げた重力モデルの欠点(i)「理論的導出が不明」を克服している(と論文には書いてあるが、似た現象からの類推でしかないのは重力モデルとあまり変わらないのではと私は思う)。
適当な指数$${α, β, f()}$$のような調整可能なパラメータを含まないので、欠点(ii)「現実の都市と合致する$${α, β, f()}$$を決めるのに最大9種類も統計量が必要」, (iii)「過去のデータから$${α, β, f()}$$を合致させても、パンデミックのような新奇な現象には合致するとは限らない」も克服している。
また欠点(iv)「似た地域で同じ$${α, β, f()}$$を当てはめても桁違いにずれることがある」の克服は図1aに示す通り。距離rだけではなく、その範囲の人口sも考慮することによって、その範囲の人口が多ければもっと近くに良い仕事があるはずだとなって、遠くまで通勤する人は減る。逆に人口が少ないと、良い仕事を探すのに遠くまで探さざるを得ない。その効果がユタ州での重力モデルと放射モデルの差に顕著に表れている。

2つの通勤路は、始点終点とも人口が似ていて距離も似ている(左下)ので、重力モデルならほぼ同じ条件だが、実際の通勤者数(右上)は大きく違う。範囲sの人口も加味する放射モデルならよく合致する。
式(2)は、距離 r ではなくその範囲の人口 s を考慮することによって、後背地の人口は有限という頭打ちも加味され、欠点(v)「無制限に人口が増えるという乖離」も克服できている。
利益 z は分布p(z)に従う乱数なので、確率的な試行を何度もすることによって流量だけでなくその分散も予測できるため、欠点(vi)「決定論的モデルであり、移住者の流動は予測できない」も克服している。(欠点(i)~(vi)まで全部克服された!)
図2は、ニューヨーク群を起点とする通勤の流れである。(書いてないが、本論文でいう通勤(commuting)は毎日通うものだけでなく、出稼ぎや単身赴任のような数か月周期のものも含むと思われる。)
重力モデルでは、明らかに近い通勤ばかりしか再現できておらず現実とは乖離しているが、放射モデルなら現実に近い予測ができている。

国勢調査(上)と重力モデル(中)と放射モデル(下)の比較
放射モデルの精度をより定量的に調べた結果が図2b~j。
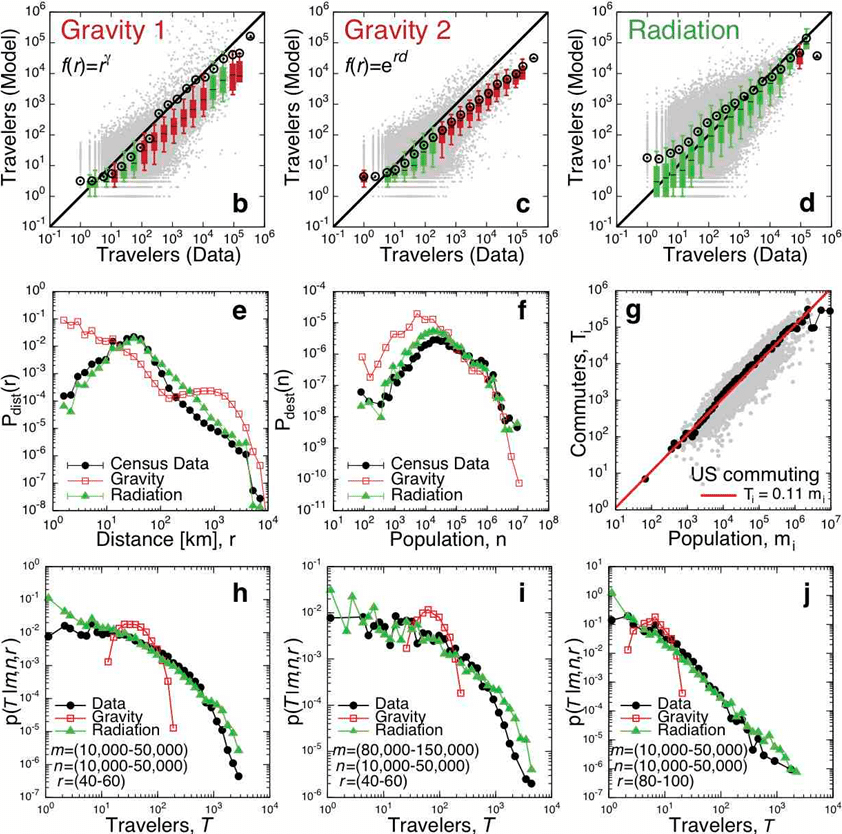
重力モデルの場合、エラーバーの範囲に収まらないデータが多いが、放射モデルならほぼエラーバーに収まる。
e. 移動距離とその移動が発生する確率 f. 群の人口とそこから出ていく人の割合
h~j. 条件付き確率 出発地と目的地とその距離(左下)を変えている
距離rにおいて、人口mの場所から人口nの場所へのT人の通勤の流れが観測される条件付き確率p(T|m,n,r)も重要な指標となる。
重力モデルでは平均近いところにピークを持った分布になってしまうが((1)によれば、同じ(m,n,r)をもつ場所のペアは同じフラックスをもつからである)、放射モデルなら現実に近い分布となる。
放射モデルは、通勤の人の流れだけでなく、電話の発信/着信、商品の輸送にも成り立つことを示しているのが図3a~l。

下:税務書類の移動

下:物資輸送
このような、通勤の人の流れだけでなく多様な性質を持つ統計量との一致は驚くべきことであり、モデルの背後にある仮説が、直接的または間接的に、モビリティや交通駆動型の幅広いプロセスに関連する基本的な意思決定メカニズムを捉えていることを示唆している。
最後に、各主要都市が多くの雇用を生むために、地理的距離を大きくゆがめてそれら主要都市へ通勤の流れができている様子を、ユタ州とジョージア州から見た”通勤風景”として眺めてみよう。

その群からの単純な距離を色で表し(a,d)、通勤人数の多い群ほど近くに図示したのがb,e、それらを拡大したのがc,fである
Clayton群から見るとロサンゼルス、シアトルが青い筋として食い込み(遠いわりに通勤者が多い)、
Davis群から見るとニューヨーク、アトランタ、マイアミが青い筋として食い込んでいる
都市間の人の移動が、一般の原子集団における放射吸収の法則に当てはめると放射モデルという、前回説明した恒星でのエネルギー放射に酷似した法則に則っている。できるだけ良い職を求めた結果の通勤をすることによって、放射の法則が成り立つ移動が起き、それが都市の起爆剤としての活動となり、国全体として太陽のようにエネルギーを拡散し、生産性を生み出す。それが見事なほどに太陽と同じ放射吸収の法則に則っている。
私たちが都市を移動することがまさに、統計力学の不思議世界探索と言えそうだ。
(新年一発目は、初心に帰るようなことを書きたかった!)
最後まで読んでいただきありがとうございます。気に入っていただけたら「スキ」ボタンを押したりフォローしたりしていただけますと私のモチベが上がります。内容についての質問や感想もお待ちしております。
また、研究機関には所属せずにやっておりますので、有料ジャーナルのアクセス料程度のサポートをいただけるとありがたいですし、今後の記事の質が上がるかもしれません。どうぞよろしくお願いいたします。
