【CADプログラミング】実践 3Dセンサ活用時のスプロケットのr-θ特性の求解法
〇 概要
スプロケットを使った演習を行います。
まずは、スプロケットのモデルを画像化するために必要な数値計算を簡単に押さえておきましょう。とはいっても、扱う数学は高校~大学初等レベルで十分追いつきます。
〇 目的
下図のように、スプロケットの側面部を観測面に設定したときに、その観測面の深さ情報が出てくるようなデータを生成します。ただし、スプロケット全面を回すため、スプロケットの周りをモータを使って常に回転し続けるものとします。
今回検証はしませんが、これを3Dセンサで測定すると、両方のデータを比較したりアルゴリズムの検証に応用できそうです。
![]()
〇 測定点の求め方
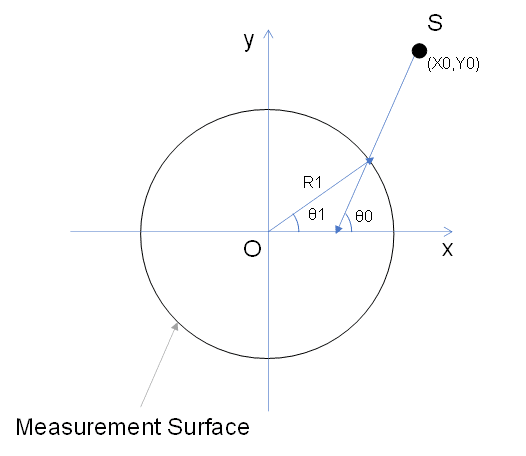
測定点である点S(X0, Y0)が3Dセンサだったとき、通常Sからスプロケットに向かった時の角は中心からやや外れることになります。そこで計算したX軸との角度をθ0, 真円の中心から測定面までの角度をθ1とすると、
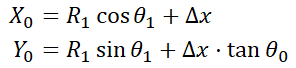
で表されます。ただし、測定点Sは測定可能な部分であればどこをとっても良いので、Sがなす軌道は直線となります。Δxは直線の従属パラメータです。
〇 測定面との交点
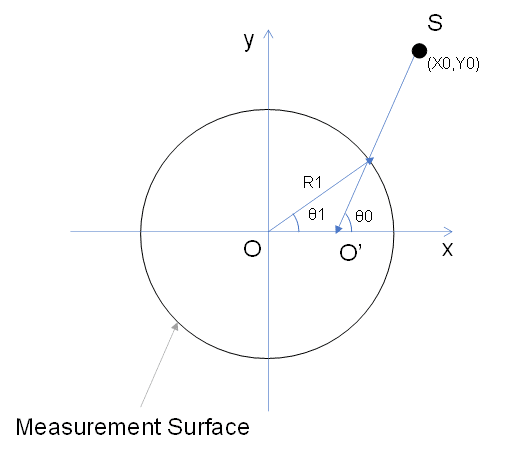
今度は、測定面と点Sがなす直線の交点を使って、測定面との交点を出しましょう。X0, Y0はΔxが自由な直線ですが、この式を書き換えると、以下の式の連立方程式となります。
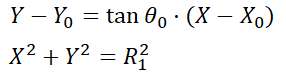
従って、ここの式に代入し、2次方程式を求めることで測定面と点Sがなす直線の交点を算出できます。
ここで一つ問題があるのですが、2次方程式の解が実数解の場合、どちらが正しい解なのかが問題になります。ですが、基本的にθ1が0であれば、x > 0の領域においては常にxの高いほうが交点となります。したがって、回転行列θ1をかけておき、そのときの二次方程式の解を使用すれば、上記の解の選択は実現可能です。
〇 スプロケットの回転
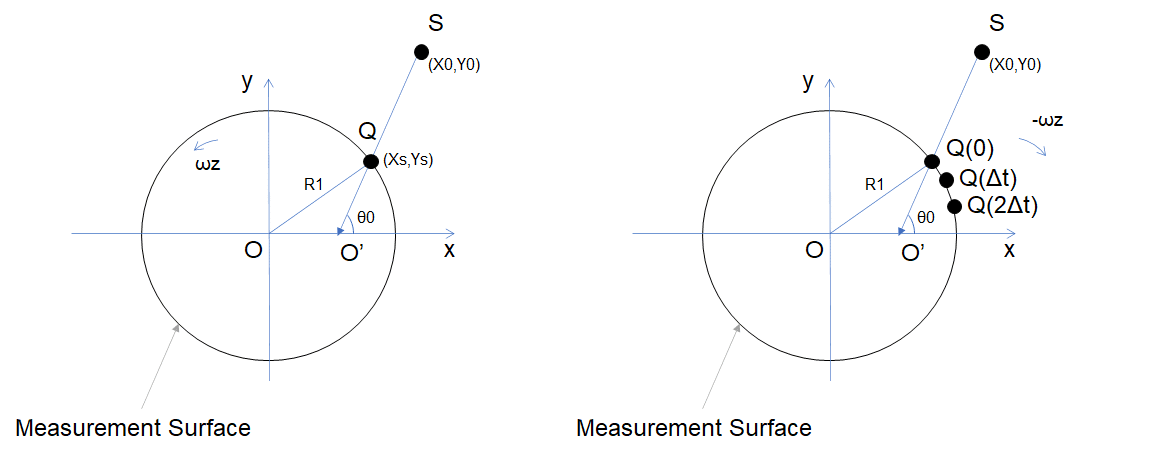
CADモデルがωzの角速度で、z軸周りで反時計回りに回転しているものとします。このとき、CADモデルが動くのが正確な表現ではありますが、CADモデルが動く、という風にするとCAD上で定義されているすべての点の交点が回転しているようなコーディングをする必要があるので、これは汎用的ではありません。
このような場合は、代わりに測定点Sが-ωzでz軸周りで回転するものとして検討します。したがって、サンプリング周期をΔtとしたとき、Qは-ωzでサンプリング周期Δtで動き続け、回転行列をRとすればR(-n×ωz×Δt)を作用させることになります。
〇 測定面との交点(直線の場合)
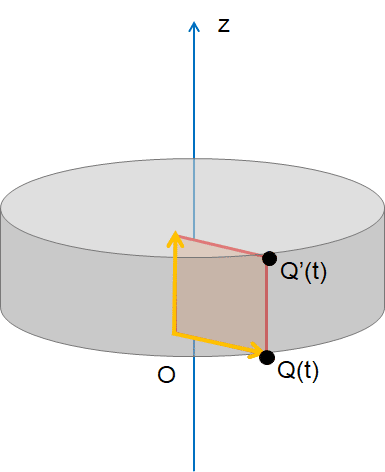
測定面との交点で、z=0のものをQ(t), zが端にあたるものをQ'(t)とします。この場合、明らかに測定面の1つ目は-ωz×tで回転している成分となり、もう一つはz軸との単位ベクトルとなります。
とりあえずt=0の場合で求めてみると、平面の単位ベクトルは
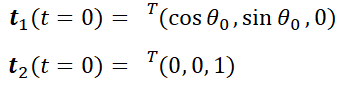
平面と測定面上の交点を表すベクトルは
![]()
さらに、一般的な回転を考える場合は
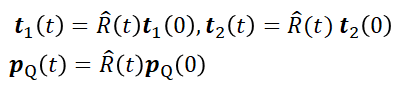
の形式で表されるでしょう。
〇 定義されているEdgeの検索
モデルは点と曲線の集合で構築されるものを取り扱うのですが、一旦曲線は直線であるものとして近似します。曲線の場合については、次のシリーズで取り扱う予定です。
ここでは、とりあえず直線の近似で、"Edgeを検索する"ということを考えましょう。これはモデルとの関係性の問題によっては、成立しなくはなりますが、ざっくりどの交点にいるかが分かりますので、簡易的なアルゴリズムとしては使えると思います。
(複雑なケースについては、研究されているものと思いますが、私にはあまり情報がありません・・・ ←要調査)
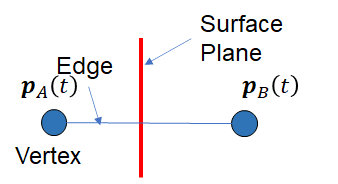
さて、この場合のQ, Q'がなす平面が、モデルの中に定義されているVertex, Edgeと重なる条件について考えます。と言っても、これは単純な平面と直線の交点であるので、3元連立方程式の解が固有の解として求解可能であり、かつすべての解が変域に収まっていることが条件となります。
具体的には、
![]()
![]()
において、(s1, s2, s')の連立方程式になるので、それが一意であり、かつp1(t), p2(t)に対して、p(t)の位置の関係性を満足することが必要となります。
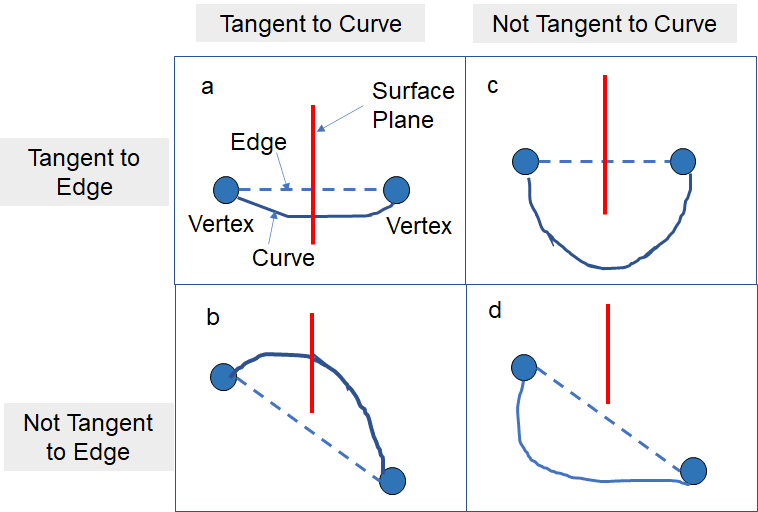
ただし、このようなEdgeの検索法をとる場合、もしEdgeがCurve(曲線)となっている場合は検索されない可能性が出てきます。
具体的には、a, c, dの場合のように、検出したい測定面と重なっている場合は問題ありませんが、
bの場合については、本来曲線として検出しているのに直線として検出不可能、という課題が発生しています。これを避けるには、単純には有効な変域を広げるのが良いと思われますが、私自身もどういう案がいいのかを検討していきたいと思っています。
〇 一般曲線の交点の求解について
曲線は代表的なケースでは、円弧、B-Splineなどが存在します。ですが、基本的に交点演算はざっくり、次の式になります。
![]()
![]()
2番目の式を要は求めればいいのです。
式としては一見単純で、これは2変数の方程式の問題、つまり2変数のNewton法が活用できそうな予感がします。ただし、ここで2変数のNewton法を採用する場合、もともとのgの形によっては発散する可能性もあるし、初期値選定を十分にしなければ収束しないでしょう。このあたりも、情報は私はあまりないのですが、調査出来ればやってみたいと思っています。(詳しい方、教えてください)
※予想ですが、g(s1,s2,s’)=0のような形になるかも。そうなると2変数ではなく、3変数になるかな。ただ、s'に関わるパラメータが非線形な特性になるので、それがどう効いてくるかが最大のポイントでしょうね。通常のSplineなら、なんらかの次数を持った特性になるので、その性質をうまく使えれば、なんとかなるかもと予想。
また円弧の場合については、もう少し問題が単純になります。(※時間を置いて円弧の交点演算についての算出を投稿したいと思います)
ここまでの内容があれば、だいたいはCADモデルの軸回転の画像化が可能になると思います。次以降で、具体的な実装上の注意に触れたいと思います。
