２次方程式 【因数分解できないパターン（解の公式）】

［前のページ］２次方程式（因数分解できるパターン）

前のページで「因数分解できるパターン」の２次方程式をやりました。
因数分解さえできたら、意外と難しくなかったんじゃないかな？

このページでは、前のページに似てるのに、
因数分解できないパターンをやります。

これも、見た目ほどは難しくないです。

ーーーーーー

因数分解できるパターンはこんな感じでした。

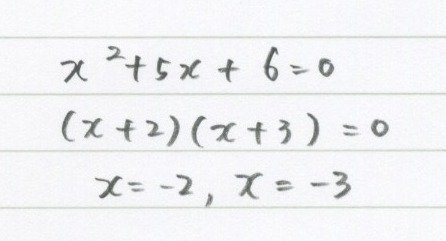
とにかく因数分解して、そしたら答えだったよね。

ーーーーーー

じゃあこれ。

あ、因数分解できないよね。
できないよね？！（分かるよね？）

因数分解できないんだから、因数分解のパターンは使えません。
こういうときは「解の公式」というのを使います。

知ってる人は知ってるこの「解の公式」。
見た目がちょっとあれなんだ。
だけど「見た目でやられないこと！」何度も言ってるね。

さあ、いくよ！

はい見た目でやられない！

英語の不規則動詞や I my me mine なんかもそうだけど、
こういうのは連呼（れんこ：何度も読むこと！）するしかないんです。
連呼してれば覚える。連呼しなければ覚えない。連呼しよう。今！

（上の式を見ながら）

「エックス　イコール　にーエー　分の　マイナスビー　プラスマイナス　ルート　ビー２乗　マイナス　よんエーシー」
「エックス　イコール　にーエー　分の　マイナスビー　プラスマイナス　ルート　ビー２乗　マイナス　よんエーシー」
「エックス　イコール　にーエー　分の　マイナスビー　プラスマイナス　ルート　ビー２乗　マイナス　よんエーシー」
「エックス　イコール　にーエー　分の　マイナスビー　プラスマイナス　ルート　ビー２乗　マイナス　よんエーシー」
「エックス　イコール・・・

はい覚えましたね。（覚えました？）

じゃあ今度は、その使い方です。
大丈夫。もっかい問題を見てみます。

やっぱり因数分解できないね。
だから「解の公式」です。
慣れるまでは、直接書いちゃうのがいいです。

そしたら代入します。
ａ、ｂ、ｃの説明をしてなかったね。
簡単です。

だから「ａ＝１」「ｂ＝５」「ｃ＝１」です。
それを代入していきます。

このとき、「計算しておかないこと」がポイントです。
５²や２×１とかもそのまま。
そのまま代入してください。

んじゃあ、とりあえず簡単なとこだけ計算します。

んであともう一息。

これで答えです。
これで答え？
うん、大丈夫です。変に見えてもね。

２次方程式は「２つ」答えが出るんだったね。
これも「±」があるから、
プラスバージョンとマイナスバージョンの２つ、答えがあるってことです。

ーーーーーー

【計算ミス、ケアレスミスを減らす方法】

慣れてきたら解の公式は書かなくてもいいです。

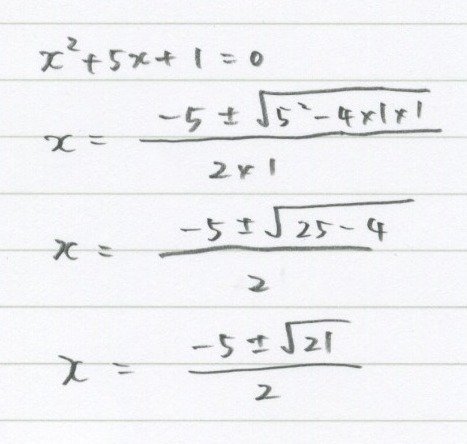
こんな感じでね！
（慣れるまでは書いたほうが絶対いい）

だけど、書かない分、２行目は必ず「そのまま代入」をしてください。
「計算しないで代入だけしてください」っていうことね。
これさえ書けば、「毎回解の公式を書いてる」ことと同じだから。

分かる？
解の公式は、忘れたらアウトの公式。
だから、毎回「そのまま代入」することで、忘れないようにしとくんです。
数カ月後、数年後のテストでも、覚えてられるように。

いきなり計算。これは絶対にしないこと。
計算ミスしたほうが面倒くさいって、そろそろ気づいてね。

ケアレスミスに注意、なんてみんな言うし、みんな知ってるんだ。
でも、「ケアレス（不注意）」のミスを「注意」するのって、どうやるの。
一生、集中したままって可能なの？ってこと。

だから、間違えないようなやり方を、解き方の中に組み込んでおくんだよ。
そしたら、集中してなくたって、間違えなくなるし、忘れなくなるからね。

だから解の公式は、必ず「そのまま代入」すること。
約束です。

ーーーーーー

本題に戻ります。
マイナスがある場合！

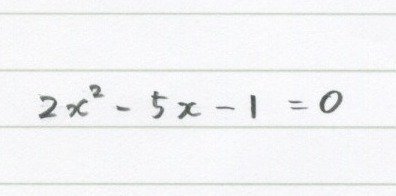
これも因数分解できなそうです。
だから解の公式に「そのまま代入」。

マイナス（負の数）を代入するときは、
こんなふうにカッコに入れて代入すればいいだけです。
こういうところでゴチャつくから、計算しないでそのまま代入してね。

代入したら、あとは計算するだけ！

こんな感じでした！

ーーーーーー

【ルートが外れるパターン】

これ、さっきのやり方で解いてみてくれる？
解いてみると、ある壁にぶつかります。
ぶつかるかな。

ルートが外れてしまいました。
（ルートが苦手だったら下のページを先にやろうね）

ルート外れたら、「±」がそれぞれ計算できそうです。
こんなふうにね。

こうやって、プラスバージョンとマイナスバージョンを分けて書きます。
まとめるね。

長いけど、

　①因数分解できない
　②だから解の公式
　③ルートが外れたからそれぞれ計算

ってしただけです。
長いからって、見た目でやられないでね。

ーーーーーー

【約分できちゃうパターン】

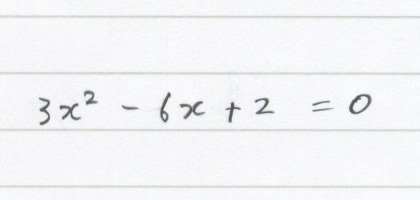
これも解いてみてください。
解の公式もそろそろ慣れたかな。

ルートも整理して、ここまで来ました。
これって、このあと計算できる？できない？

約分が「実は」苦手な人が多いの、俺は知ってるぜ。
実はどきどきしながら毎回やり過ごしてるの、知ってるぜ。

めっちゃ分かりやすく書いたから、不安な人は先に下のページ。
「ハートの法則」を身に付けたら戻ってきてください。

ということで、さっきのは「ハートの法則」で

これで答え、ということでした。

意味分からなかったら約分のページ絶対やってきてね！
因数分解も解の公式もできるのに、なぜか発生するケアレスミス。
それは「約分で間違えてる」可能性があるよ。
つまりそれはケアレスミスじゃないからね。

ーーーーーー

実は、２次方程式はもう、
「因数分解できるパターン」と、
「因数分解できないパターン（解の公式）」で、ほぼおしまいです。

ちなみに、どっちのパターンも、

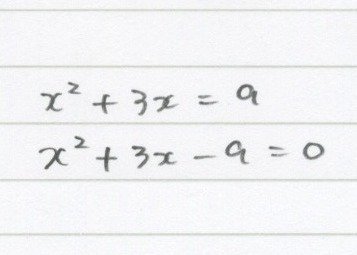
ちゃんとこうやって「＝０」にしてからね。

（ちなみに、因数分解できるパターンも解の公式で解けます。
　つまり解の公式は（めんどいけど）なんでも解ける）

次のページで、２次方程式最後だ！
じゃあ練習やって、次にいこう！

［練習問題］式はまずノートに写そうね（答えは下）

［全ページに飛べるもくじ］

［次のページ］２次方程式（ｘ²＝◯のパターン）

［答え］

解の公式、ちょっとめんどくさかったね。
よくがんばったね。