
VR楽器「isonote」 〜深い話編〜
〜概要・紹介編〜からだいぶ間が空いてしまったけど、ようやく、このVR楽器がどういう楽器なのか、数学と音楽の観点から考える〜深い話編〜に入ります。新しい楽器の設計を通して音や音楽について学ぶという、あまりない面白い話になってるんじゃないかと思います。
ただし、ふつうに音楽教育を受けたり音楽理論を学んだ人にとってはありきたりな話か、あるいは定説から外れた邪道かもしれません。とりあえず、私が無からいろいろ考えた軌跡を記します。
1. 使う音律について知る
なぜオクターブは12音なのか
私たちが日常的に接している音楽はほぼ全て「1オクターブが12音な世界」の内側で生み出されている。ピアノは白鍵7つ+黒鍵5つだし、ギターも12フレット。例えばバイオリンなどフレットレスな楽器も、正確に12音を押さえる練習をする。もちろん楽器だけでなく、五線譜もカラオケのキー調整もDTMで音を打ち込むピアノロールも、何もかもが12音前提でできている。それならば、今から作る新しい楽器も、一般的な音楽世界に接続するためにこのルールに従う必要がある。
ただ、ここでいきなり“謎”に直面する。
そもそもなんで1オクターブは12音なのだろう?
新しい楽器に「12音ルール」を採用するのは良いが、私が作りたいのは「音楽の構造が誰にでも視覚的にわかった上で弾ける楽器」なので、ルールの中身もちゃんと把握しないといけない。
というわけで、この謎についてあれこれ調べた結果、最終的に私が行き着いた結論がこれ。
「たまたま、3/2の12乗が、2の7乗に近かったから…!」
なんだそれはという感じだけど、3/2の12乗 = 129.7463…は、確かに2の7乗 = 128に近く、誤差1%程度なのは事実。この数字は何を意味するのか?
音 = 波
そもそも、音は波である。…ということを、人類はいつ知ったのだろう。
たぶん管楽器より弦楽器のほうが目で波を見ることができるので、大昔の暇な人がピンと張った固い糸をはじいてみて気づいたんじゃないかと、勝手に想像している。
で、音は波なので整数倍というものが大きな意味を持つ。基準となる音に対して整数倍の周波数となる音を倍音と呼び、弦でも管でもある音を鳴らした際には、基音のみならずこの倍音たちも必ず一緒に鳴るらしい。
弦で倍音を探すのは簡単で、
2倍音は、弦長を半分にすれば鳴る、ちょうど1オクターブ上の音。
3倍音は、弦長を1/3にすれば鳴る、1オクターブより上のいい感じの音①。
4倍音は、弦長を1/4にすれば鳴る、ちょうど2オクターブ上の音。
5倍音は、弦長を1/5にすれば鳴る、2オクターブより上のいい感じの音②。
6倍音は、弦長を1/6にすれば鳴る、2オクターブより上のいい感じの音①。
ここまで書いてわかるのは、「素数」以外はいらないということ。4倍音や6倍音は、2倍音や3倍音で表すことができる。自然数は素数の積で表せるので、2, 3, 5, 7, 11倍…の響きがわかればあとはその組み合わせでいい。
ピタゴラス音律
数に美しさを求める人間は、7や11や13という数字に出てきてほしくはない。2と3のふたつの素数があれば十分だ。2対3、この美しい整数比だけで音の世界を表そう。と考えたのが「ピタゴラス音律」だと思う。

この世の音をすべて「2のx乗 × 3のy乗」で表すことにする。原点(x,y) = (0,0)を基音とすると、オクターブ内、つまり基音と2倍音のあいだ(=解が1と2のあいだ)に収まる(x,y)の組は、たとえば(-1,1)や(-3,2)など、無数に存在することがわかる。これを模型にしてみると、一直線上に無限遠まで音が生まれているのが観察できる。ピタゴラス音律においては、オクターブ内の音は12個どころか、無限に存在することになる。
しかし、ここで先ほどの「3/2の12乗が、2の7乗に近い」という偶然が効いてくる。この誤差を無視することにしてしまえば、無限にあったオクターブ内の音は、丸められてたったの12音になる。
もちろんズルをしているので、ほんとうは微小にズレた12音が無限にあり、同じドでも「ちょっと高いド」や「常人にはわからないが極めて微妙に低いド」等が存在するのだが、それらをなかったことにしちゃう。
このように、ドにとって最高に美しいソ、ソにとって最高に美しいレ、というように繰り返していったらなんか12個目でそこそこいい感じにドに戻ってループしたっぽいので、人間も慣れ親しんでる数字だし12でいいじゃん、というのがオクターブが12音な理由です。(たぶん)
オイラーの5リミット純正律
2:3という整数比の美しさにこだわったピタゴラス音律だが、その純血さがかえって美しくない結果を生むことに皆薄々と気づく。というのも、ピタゴラス音律の世界では2と3しか使えないので、あの単純なドミソを整数比で表そうとすると、2の6乗:3の4乗:2の5乗×3 = 64:81:96になってしまうのだ。実際は数字の複雑さの問題ではなく演奏上の不協和が無視できなくなって、これを解消すべく「純正律」というものが考案されることになる。(中全音律というのもあるけどここでは割愛)
純正律についてWikipediaで調べれば、「純正律の長調の全音階は、純正完全5度(3/2)と純正長3度(5/4)を用いて…」と書いてあるのだが、これだと音楽理論の用語だらけで難しい。それに、私はこの説明の意味がわかった後でも、この説明があまり好きじゃない。ピタゴラス音律と純正律とで名前が全然違うのもしっくりこない。単に、2と3だけでなく、次の素数「5」までを許した世界、と考えるのが一番シンプルじゃん、と思う。この考え方に沿った純正律の呼び方が「オイラーの5リミット純正律」だと思われる。使う素数を5までにした、という意味。

この世の音をすべて「2のx乗 × 3のy乗 × 5のz乗」で表すことにしなおした。5を手に入れたことで、ドミソを4:5:6で表したり、ラドミを10:12:15で表したりできるようになり、ピタゴラス音律よりもだいぶ綺麗になった。それ自体はなんとなくめでたい。
しかし、相変わらずオクターブ内に無数の音が生まれてしまう問題は解消していない。こちらも模型にしてみると、3次元上のある平面付近に無限遠まで音が生まれているのがわかる。この無数の12音の存在が相変わらず悪さをしてしまう場面に、演奏者たちは出くわす。
平均律
ピタゴラス音律も純正律も、局所的な美しさ(単純な整数比)を優先した結果、その「美」から距離が離れるほど歪みが増大するシステムなのだった。その美学を捨て、ある程度それっぽければ良しとする代わりに、12音を本当に12個にするという機能性を優先したのが「平均律」である。音と音の間隔を「2の12乗根」で完全に均等にすることで、整数比はどこにも存在しなくなるが、代わりに、どこから弾いても、曲の途中で転調しても問題が起きないモダンで便利な12音を手に入れることになった。

平均律の模型は一気に単純化する。これは12まで数えると一周して閉じる円環なので「mod 12」である。mod 12は、12で割った余りが一緒のものは同じとみなす、という数式で、例えば 1 ≡ 13 (mod 12)というふうに使う。さらにここでは「7n (mod 12) 」(nは任意の整数)とすることで、ピタゴラス音律の2:3にかなり近い、1:約1.4983の関係にある音を隣にして一周ならべなおす。2の12乗根の、0乗→7乗→2乗→9乗→…という順に円を一周させる。この並べ方は、平均律でありつつ、ピタゴラス音律をリスペクトしたようなものだと思えばいい。
ここまでのまとめ。
1オクターブが12音なことは、数学的な偶然と、人間の恣意性によるものだった。ただ、12音と決まった以上、もう12音ありきで整えちゃおうという発想により、平均律に至った。これで、isonoteが採用する「12平均律」というものの意味や成り立ちを理解することができた。
2. 12音をどのように並べるか
五度圏表
最終的に楽器としてまとめるには、なんらかのルールで音を並べなくてはいけない。次の課題は、12音をどのように並べると、音楽的に意味があって、かつ演奏できる楽器になるのか。演奏については3章で扱うとして、ここでは「音楽的に意味のある並べ方」について考えてみる。
音楽についていろいろ調べる中で何度もお世話になったものの一つに、「五度圏表」というものがある。この円盤状の表はポピュラー音楽の理論でよく出てくる便利グッズで、ある曲のキーが分かれば、そのキーの音階でつくられる7つのコード(ダイアトニックコード)が一目でわかるという代物。あと地味に、楽譜にシャープやフラットがいくつ付いているか見ればキーがわかる、という使い方も便利。音楽理論についてあれこれ調べる中で、私もこれは実用的だし面白いなぁと、だいぶ読み込んだ。

この表には外、中、内の3つのリングがあり、それぞれに、C、Am、Bm(♭5)などといった「コード」が記載されているのだが、このうちの外リングはさきほどの「12平均律の模型」と全く一緒だ。というより、それもそのはず、12平均律を「7n (mod 12)」で並べ直したのは、むしろこの五度圏表を私が真似したからだった。たしかに便利だし、ピタゴラス音律リスペクトで意味のある並びだからとこれに倣った。
五度圏表が不純に見えてくる
でも、私はだんだんとこの表の、実用に優れているんだから「こまけぇこたぁいいんだよ感」がどうしても気になってきてしまった。外リングは論理的だ。というより、どのリングも単体で見れば「7n (mod 12)」の並びなのでわかる。でも中リングはなぜ「m」がつくマイナーコードで、その場合なぜ並びが90度ずれるのか、内リングはなぜ「m(♭5)」がつくマイナーフラットファイブコードで、その場合はなぜ150度ずれるのか。
また、あるキーの7つのコード(ダイアトニックコード)を読み取るときに、なぜ外リングと中リングからは3つずつ取り出して、内リングからは1つだけなのか。公平じゃなくない?とか。
たぶん実用派のひとは、「いやいや、なぜ?じゃなくて、便利になるように並べたんじゃん…」と言う気がする。違うんだ、私はそれはイヤで、ただ論理的に並べた結果、自然と意味が浮き彫りになるという順番が良いのだ。
isonoteの初期モデル
五度圏表は、便利さを優先した結果、本来見えてくる音と音の関係=構造が見えにくくなっている。なんで3つリングがあるのかの説明もない。そこで私は、平均律によって一度閉じてしまった円環をもう一度、ピタゴラス音律の考えに戻って開いてみることにした。
そうしてできた以下の表こそが、isonoteの「初期モデル」となった。

C(ドの音)を中心に、単純に右と左に周波数比2:3の音を並べていく。この表の上のほうはCメジャーキーを表していて、音階に出てくる7音は「F C G D A E B」の順になる。「ドレミファソラシ」ではなく「ファドソレラミシ」だ。
このように円環ではなく横に並べると、すでにいいことがある。五度圏表ではリングで分けられていてよくわからなかったメジャーコードとマイナーコードの分布が、単純に左3つ(FCG)はメジャー系(M7や7)、右4つ(DAEB)はマイナー系(m7やm7-5)というふうに、左右で綺麗にわかれてくれた。
続いて、この表の下のほうはCマイナーキーを表していて、音階に出てくる7音は「A♭ E♭ B♭ F C G D」。注目する位置を変えただけで、メジャーコードとマイナーコードの分布に変化はない。
それから、メジャーからマイナーにするにあたって注目点を左に3つ移動したので、音階に出てくるフラットの数も3つになった。同様に右にN個動かせばN個シャープがつく。五度圏表よりよほど素直でわかりやすい。
モードもわかる
というわけで、メジャーキーとマイナーキーはこの左右移動だけで表現できたのだけど、さらにこの表を使えば「モード」の理解も簡単になる。
「モード」と言われるとちょっと難しい音楽理論のように聞こえるけど、この表においては単純で、C(ドの音)が含まれるように、色付きエリアをどこに置くか考えると、7通りの置き方があるよね、というのが「モード」。
とくにこの基本の7通りはチャーチモードと呼ばれ、元々は古い教会音楽のなかで発展したものだけど、モーダルジャズの出現以降、一般的に用いられるようになった。たぶん。
例えば、Cが色付きエリアの中心にくるように置けば、Cドリアンモードになって、そのモードで使用する音も、生まれるコードも、臨時記号(シャープやフラット)の数も、全部一発でわかる。

ちなみに、7種のモードで捉え直すと、CメジャーはCアイオニアンモード、CマイナーはCエオリアンモードと呼称が変わる(厳密には呼称の問題ではなくて概念から違うけど一旦無視)。そして色付きエリアを右にするほど明るい響きになり、左にするほど暗く沈んだ響きになる。基準となる音から見て、右寄りの7音を選ぶか左寄りの7音を選ぶかで、響きの明暗がグラデーショナルに変わるのだ。これが個人的にかなり面白くて大好き。
「フリジアンモードは、ダイアトニックスケールを第3音から弾いた時のモードで〜」とか言われてもよくわからんのだけど、「マイナースケール(エオリアンモード)より1個左だから、1個分さらに暗い響きで、フラットも1個増えて4つになるよ」の方がめちゃくちゃわかりやすい。
さて、これで12音を意味のある並べ方でまとめる、とても素直で良い表ができた。
3. 演奏するための音配列
ホールトーンの出現
良い表ができたところで終わってはいけなくて、目的は楽器をつくることなので、ここから人間が演奏できる楽器をつくらなければならない。
いろんなことがクリアになる音の並びが「ファドソレラミシ」だということはわかったけど、これをそのまま鍵盤にして演奏するとなると、幼い頃から「ドレミファソラシ」を叩き込まれている人間はたぶん混乱する。かといって「ドレミファソラシ」に戻したら意味がない。
そこで、改めて、周波数比2:3(=完全5度)の並びを図にしてみる。

この図は、以下のような構成になっている。
横:同音の列(C=D♭♭=B♯などは異名同音)
縦:半音ずつ上昇
基準となるCを赤く塗ったら、1つ右は7つ上(完全5度上)を塗るというルールで色付けする
こうしてみると、「F C G D A E B」という順に塗っているのに、どちらかというと「C D E F♯…」と「F G A B…」の斜め右上に伸びていく2つの列のほうが目に見えてくる。周波数比2:3(完全5度)の図のなかに出現するこの「C D E F♯…」の列は、全音(半音2つ分)ずつ等間隔に並んだ音階なので、「全音音階(ホールトーンスケール)」と呼ばれる。
このように、5度の並びは、全音の並び×2列に分解することができる。黒枠で囲った中がCメジャーキーの7音なので、この枠内だと「CDE」と「FGAB」の2列になり、これは「ドレミ」と「ファソラシ」なので、喜ばしいことに、人間が勝手知ったるあの並びになる。

この音の配列はスプレッドシート上なのでグリッドに並んでいるが、これを三角形グリッドに落とし込んだものが、isonoteの音の並びになった。

というわけで、isonoteの模型ができあがった。
三角形グリッド平面に、高さ=周波数の柱を立てて梁でつないでみたところ、これは美しい屋根だなぁと思った。建築の上棟式でこの構造が立ち現れたら良い気分に浸れそう。
Wicki-Haiden Note Layout
三角形グリッドの各点に打面を配置することで、模型は楽器へと変わる。
〜概要・紹介編〜にも書いたように、isonoteを公開してから、全く同じ図が127年前に考案されていたということをTwitter経由で知った。

これこれ、これ、完全にこれ。
長い思案の先にたどり着いた配列が、これだった。三角形グリッド上に蜂の巣状の打面としてFCGDAEBを並べていくとこの図とまったく同じになる。そして、この図の右に書かれているように、すべての音が、どこを起点に取っても均質に、以下の関係を持つ。
右横:全音上(周波数比8:9)
右上:完全五度上(周波数比2:3)
左上:完全四度上(周波数比3:4)
上:オクターブ上(周波数比1:2)
こういう数学的な音の配列を、クロマチックキーボードというらしい。そういうのも公開後にTwitter上で教えてもらった。isonoteを見て、これはバンドネオンだ、クロマトーンだ、大正琴だと、いろいろ引用リプをもらった。やっぱりTwitterいいですね、頑張れTwitter。
VRで和音を演奏したい
さて、音の配列は定まった。次に必要なのは、実現したい演奏法と、それを可能にするインターフェースを考えることだ。
VR空間でアバターを用いて楽器を演奏するという前提に立った時に、ピアノやギターのように10指をつかって精密に弾くということは、デバイスの制約上まだ望めない。VR空間で演奏するとしたら、鉄琴や木琴のように2本のバチで打面を叩く動作くらいの大雑把さを前提にしないといけない。
ただ、問題は私が「和音を弾きたい」と考えていること。2本のバチで2音以上の音を弾くことをどうやって可能にするか。また、例えばCM7(メジャーセブンス)のような、よく使われる4和音を弾けることも必須条件にしていた。
ここでこそVRが活きてくる場面なのだが、バチが同時に1点しか叩けないのだとしたら、打面のほうを重なり合わせればいいじゃん。という発想を、VRは許してくれる。
isonoteの三角形グリッドの音の並びでは、打面を互いに重なるように広げれば、1ストロークで同時に最大3音鳴らすことができる。そしてこの配列は関係の深い音が隣接するような音の並びになっているので、幸い2本のバチがあればCM7やCm7といったコードを弾くことができることがわかった。左手のバチでCとGを同時に叩きつつ、右手のバチでEとBを同時に叩くことが可能なのだ。
以下は、ベン図のように重なったところを叩けば同時に複数音鳴らせることを利用した、isonoteのコード表である。(円のなかの文字は、そのコードのルート音=Rからの音程を表す表記になっています)
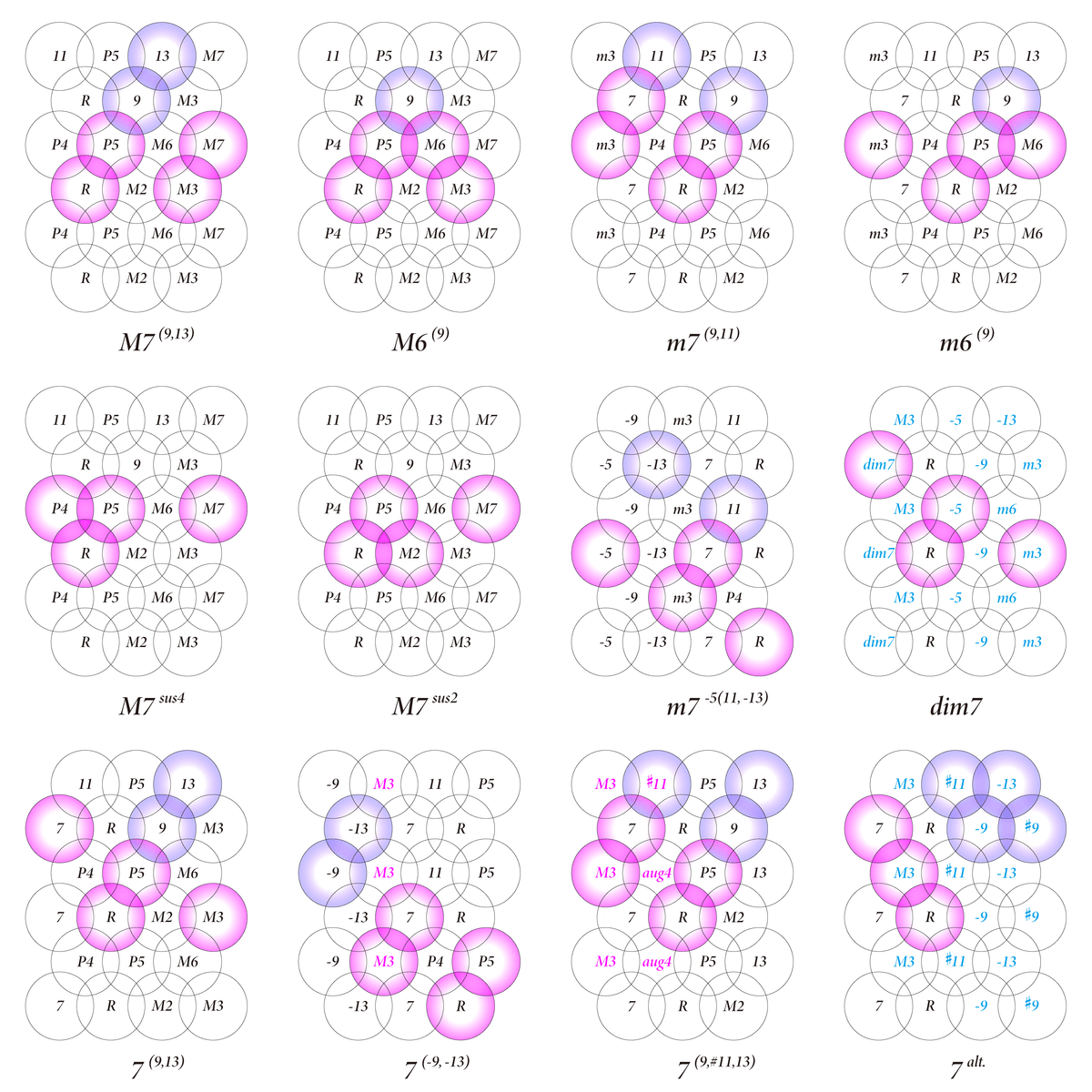
ピンクがコードトーンで、紫がテンションノートを表す
※ただし、ノンダイアトニックコードの押さえ方は最新版ではこの図から変わっている。後述する。
ひとつ残念だったのは、最も大事なセブンスコードや、m7(♭5)コードは2本のバチだけでは同時に叩けないことが判明したことだった。これらのコードは曲の進行の解決の直前に使われる不安定なコードで、コード内に全音3つ分開いた関係の最も遠い音(トライトーン)を含むタイプのコードなので、例えばG7コードではBとFを叩かねばならず、isonote上では距離が遠いために同時押しができなかった。
ただ逆に言えば、今言ったようなことも音配置としては正しく表現されていて、安定なものは距離が近く不安定なものは距離が遠いというisonoteの特徴を裏付けるものだと言える。
こうして、isonoteは完成した。

4. 半音弾きにくい問題
isonoteの音配列の弱点
こうして無事にVRChatに公開できたisonoteだったが、実は公開直後と今とで大きく機能を変えた部分がある。それは「半音」の扱いだ。
isonoteは、周波数比2:3(完全5度)で並べることで関係の深い音と音を近づけているため、適当に弾いても非常に調和の取れた音を鳴らすことができる。ピアノやギターを目の前にして「なんもわからん」となる人でも、いくつかのコツを学ぶだけですぐにいい感じに弾けるようになる。それは最大の強みである一方、調和から外れた音へと抜け出しにくいという問題が、この配列(=半音が隣にない配列)にした以上どうやっても解決できない壁として立ちはだかる。
調和から外れた音というのは、音楽が豊かであるためになくてはならないもの。isonoteでは隣り合う7音が基本の7音(ダイアトニックスケール)になるが、その外側にある音や和音(ノンダイアトニックコード)が差し込まれることで、曲がドラマティックに変化したり、緊張と弛緩が生まれる。予定調和から抜け出すことができる。
なかでも特に使用頻度が高いのが、クラシック音楽の時代から使用されている「ハーモニックマイナースケール」と「メロディックマイナースケール」という2つのいびつなマイナー系スケールで、これが気持ちよく弾けないと、ポップスもジャズも演奏ができない。しかしこの2つの音階は、isonote上だと「隣り合わない7音」になるため、演奏者が弾き方をスッと認識しづらく、使いこなすにはかなりの鍛錬を要する。…というより、半音が隣接するピアノやギターに比べると単に弾きにくい。
苦し紛れの半音上下
公開当初は、上記の2つの特殊なマイナースケールを隣り合う7音の中で叩けるように、VRコントローラーのサムスティックの上下で、一部の音を半音上げ下げできるようにしていた。(正直この設計にしたことで、めちゃくちゃ工数がかさんだ…)

しかしやってみて思ったのは、やはりせっかくの論理的な音の並びを部分的に歪めるのは美しくないな、という気持ちだった。既存の楽器が生み出してきた音楽のために、この楽器の構造を歪めるのは、なんか違う気がした。この楽器にはこの楽器だからこそ弾きやすいものと弾きにくいものがある、というほうが素直だと思った。
なので、公開後にこれをやめて、代わりに「古今東西90種類のスケールを打面に表示する機能」を足した。付け焼き刃の半音上下はできなくなったが、isonoteの音の並びでは半音が遠いという事実を受け入れることにして、むしろ世界中の音階がこの配列だとどのように表現されるのか、視覚的に学べるようにした。
以下は、その機能の紹介動画と、制作したテクスチャの一部。


さいごに
10,000字に迫る長文で、ほとんどの人にとっては「何それ?」な、極めて特殊なVR楽器の解説を書いてきました。正直、ここまで読んでいただいた人は、わりと変態(褒め言葉)だと思います。ありがとうございました。
ぜひVRChatのワールドに行って弾いてみて、ここに書かれていることを体感いただけると嬉しいです。(おわり)
いいなと思ったら応援しよう!

