S&P、オルカン（全世界株式）への集中投資は本当に安全なのか？を証券投資理論で検証する

2024年4月6日 18:23

最近、新NISAの開始に伴って、資産運用ブームがきている気がします。これまで資産をほぼ現金貯金や定期預金、保険など安全資産で運用してきたマジョリティの方々が証券投資に参入してきています。

そんな投資初心者の方に向けての情報でよく目にするのが、「とりあえずS&P、オルカン（全世界株式）に投資しておけば大丈夫」という案内です。確かに、株式市場には無数の銘柄が存在していて、どれから投資したら良いのかわからない人からしたら、シンプルでとてもわかりやすいですよね。
でも、学生時代から証券投資をしている僕からすると、これ本当に大丈夫なのかな？といつも不安になります。今回はその不安を理論的に解消するべく、証券投資理論に基づいて、それらの運用方法を評価してみたいと思います。
※結果だけ先に見たい方は、まとめをご覧ください

また、いつも通り仮定を置いている部分や、僕なりの持論も含まれる内容ですので、これを見て投資をする方は自己責任にてお願いいたいます。

まずは証券投資理論の基本を抑える

証券投資理論を理解するにあたり、基本的な知識をおさらいしていきます。ややインプット多めなので、だるい人は飛ばしてください。ここを読んでいなくても内容は理解できます。

キーワードとともにまとめていきます。
リターン（期待収益率）：その銘柄へ投資することで、平均的に選られるであろう収益率。高いほど得られる利益が大きい
リスク（標準偏差）：価格変動の大きさを表した指標。一般的には危険度みたいな意味で使われているリスクだが、証券投資理論上では価格変動の幅として使われている。
相関係数：2つの異なる銘柄の値動きが、それぞれどの程度連動しているか？を表した指標、1が完全に比例していて、-1が完全に反比例している状態。
S&P500：アメリカの500の企業から構成された株価指数。S&P自体は商品ではなく、S&Pに近い動きを目的とした投資信託などが俗にいうS&P投資の商品となる。
オルカン（全世界株式）：世界中の主要な株式市場（アメリカ・日本・カナダ・欧州諸国など）によって構成される株価指数。これも同じくオルカンに近い動きを目的とした投資信託などが俗にいうオルカン投資の商品となる。ちなみに、これらの銘柄の構成比は時価総額の加重平均によって決められるので、米国株式の毛色が強い。

S&P、オルカンの収益性とリスクを理解する

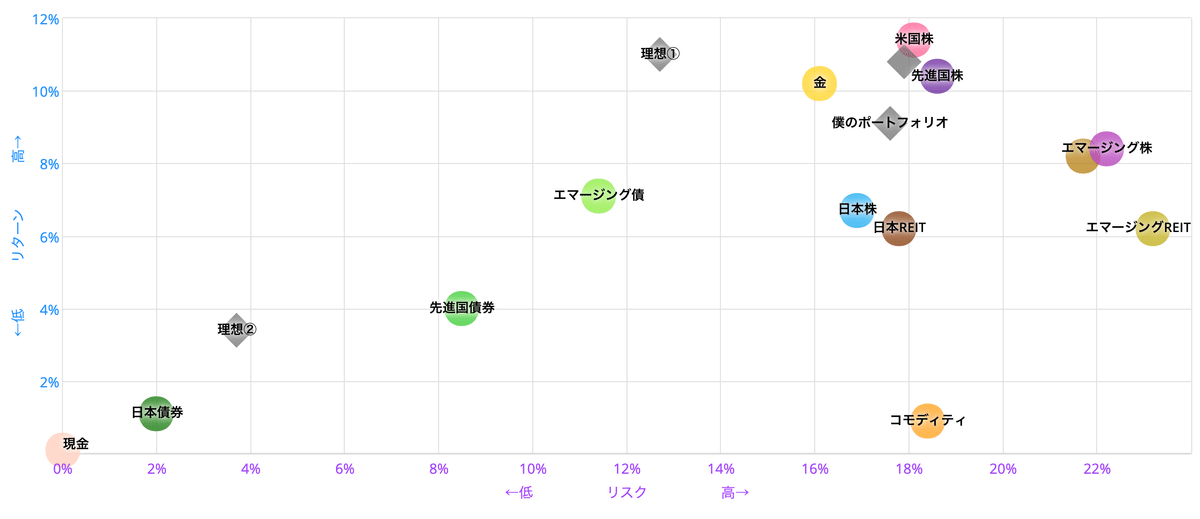
さて、古臭いやり方ですが、過去20年の実績を元に、こいつらがどういった投資商品なのかを見てみましょう。
比較に際して、筆者愛用のサイトを利用しました。

S&Pは米国株としてみてください。ついでに今の僕のポートフォリオのパフォーマンスも載せておきます。

縦軸が期待できる収益率で、横軸が値動きの大きさです。前者は高く、後者は低いほど優秀な投資先です。
こうしてみると、S&Pやオルカンはリターンが高くて価格変動幅も大きいことがわかります。
用語を見ていない人に解説すると、「平均的に期待できる収益は大きいが、値動き(マイナス含む)が非常に大きい商品」ということになります。この値動きの大きさは結局どのようなことを示しているのでしょうか？？オルカンをサンプルとして、値動きがランダムに行われると仮定して描いた確率分布は以下になります。
※Pythonにて作成。コードは最下部に載せておきます。

数学苦手な人は、「損をする確率が27%くらいある」とだけ理解してください。確かに期待できる収益は大きいですが、それほど元本割れする可能性が高いということです。

これらの商品に投資する場合は、それ相応のリスクがあることを十分に理解したうえで投資しましょう。

ではどのような投資が効率的なのか？

証券投資理論としては、これらの単一銘柄だけではなく、その銘柄と値動きがなるべく連動していない(相関係数が0)の商品との組み合わせを行ってリスクヘッジをすることが効率的とされています。※厳密にはS&Pなどの投資信託は複数銘柄を組み合わせて作っていますが、マクロで見ると米国株式市場の動きとほぼ連動しているので単一銘柄として扱っています。。

驚くべきことに、このように銘柄をかけ合わせると、リターンを大きく減らすことなく、価格変動幅を減らすことができます。

なぜこれらが効率的なのか？

証券投資理論では、リターンが最大、リスクが最小となる銘柄の組み合わせが最も効率の良い投資となります。つまり、さっきの散布図で言うと一番左上から近い構成比が最も理想的な投資になります。これは相関係数が0に近い組み合わせかつ、2つの組み合わせで得られるリターン-リスクが最大になる構成比が最適になります。

相関係数の絶対値が高いほど、この緑の曲線は直線かくの字に近づいてしまうので、組み合わせによる最適化をすることができません。（この時のリターン-リスクの値はどこでも同じ数値、つまり分散させる意味が全くない）

まとめ

検証の結果をまとめます。

S&P、オルカンなどの商品だけに投資をし続けると、収益は多く期待できるが、値動きが大きいので損をする確率も相応に高くなる。
証券投資理論に基づくと、リターンを最大限・値動きを最小限にすることで、より効率的に収益を得ることができる
理想は値動きの連動性がない銘柄を組み合わせることで、効率性を求めるなら以下がおすすめ
- ①ある程度元本割れを許容できて、たくさんの収益を得たい方
  ⭐️金50%:米国株40%:新興国債10%
  →19%の確率で損するが、期待利益率は11%
  ②元本割れを極力避けつつ、それなりに儲けが欲しい方
  ⭐️米国株20%:日本国債80%
  →18%の確率で損するが、期待利益は3.4%

そもそもですが、効率的な投資が完全に正しいというわけではありません。S&Pなどに一点投資すること自体は悪いことではありません。ただし、それに伴うリスクはしっかりと理解しておく必要があります。

また、投資をするにあたり、NISAやiDeCoがめちゃくちゃおすすめなので、また今度記事にでもしようと思います。※特にiDeCoは利益を出さなくても得をする仕組みなので、要チェック★

この記事について

タイミーで事業管理をしている福島が日々感じたことから思考を巡らせ、備忘していき、学びを積み上げていきます。あんまり業務に関係ないこともつぶやきます。

「オードリーのオールナイトニッポン 📻 で毎週フリートークしているのをリスペクトしていて週次でnote更新をしているSho1さん」をリスペクトしているので、僕も見習って週次くらいで更新し続けたいなと思っています。

LinkedIn：https://www.linkedin.com/in/takumi-fukushima-bb11331b9

Wantedly：https://www.wantedly.com/id/TakumiFukushima

おまけ：分布を描くプログラム

Python環境でnumpyとmatplotlibとscipyのライブラリをインストールしてから使ってね〜

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import font_manager

# 正規分布の確率密度関数を定義
def normal_pdf(x, mu, sigma):
    return (1 / (sigma * np.sqrt(2 * np.pi))) * np.exp(-0.5 * ((x - mu) / sigma) ** 2)

# 平均と標準偏差を指定
mu = 3.4
sigma = 3.7

# 確率密度関数を計算するための範囲を指定
x = np.linspace(mu - 3*sigma, mu + 3*sigma, 1000)

# 正規分布の確率密度関数を計算
pdf = normal_pdf(x, mu, sigma)

# 日本語フォントの設定
jp_font_path = '/System/Library/Fonts/ヒラギノ角ゴシック W3.ttc'  # 適切なフォントパスを指定してください
jp_font_prop = font_manager.FontProperties(fname=jp_font_path)

# 平均を強調して表示する点を追加
plt.plot(mu, normal_pdf(mu, mu, sigma), 'ro', label='平均値', markersize=8)

# 正規分布曲線をプロット
plt.plot(x, pdf, label='正規分布(mu={}, sigma={})'.format(mu, sigma))

# Xが0以下の領域を色塗りして、その合計をグラフ内に記載
x_below_zero = np.linspace(mu - 3*sigma, 0, 1000)
pdf_below_zero = normal_pdf(x_below_zero, mu, sigma)
plt.fill_between(x_below_zero, pdf_below_zero, color='lightblue', alpha=0.5)

# 赤点の左横、かつ少し下の方にテキストを配置
plt.text(mu - 2.8*sigma, normal_pdf(mu, mu, sigma) - 0.01, '領域の合計: {:.2f}'.format(np.trapz(pdf_below_zero, x_below_zero)), fontproperties=jp_font_prop)

# 軸ラベル、タイトル、凡例の追加
plt.xlabel('変数の値', fontproperties=jp_font_prop)
plt.ylabel('確率密度', fontproperties=jp_font_prop)
plt.title('正規分布の確率密度関数', fontproperties=jp_font_prop)
plt.grid(True)
plt.show()

0以下となる確率を計算するプログラム

import scipy.stats as stats

# 平均と標準偏差
mu = 10.8
sigma = 17.9

# 0を下回る確率を計算
probability_below_zero = stats.norm.cdf(0, loc=mu, scale=sigma)

print(f"0を下回る確率: {probability_below_zero:.4f}")