生成AIと数理的最適化を統合したフレームワークの提案とその実践: アルバイトのシフト作成における自動化と最適化

要旨

本記事では、生成AI（Generative AI）と数理的最適化を統合し、作業プロセスを革新する思考法の「OptiGen-AI」を提案する。このフレームワークは、人間による曖昧な問題定義を自然言語処理により厳密な数理モデルに変換し、動的な最適化と説明可能な意思決定支援を行う。生成AIの柔軟性を活かし、数理最適化の解法設計を自動化し、反復的改良を通じて高品質な解を効率的に生成する。本記事では、アルバイトのシフト作成といった多目的かつ動的な課題への応用を通じて、従来手法を凌駕する時間の削減効果を実証した。さらに、生成AIが提供する説明可能性により、従来人間の作業によりブラックボックス化していた意思決定プロセスを透明化する可能性も示す。本提案は、最適化分野における人間とAIの協働の新たな標準を提示し、最適化社会の実装において大きな貢献を果たすと期待される。

---

1. 序論

最適化問題は、エネルギー、交通、製造、ロジスティクスといった分野において、効率化とコスト削減を目指すための中心的な課題である。これまでの研究では、線形計画法（LP）、混合整数線形計画（MILP）、遺伝的アルゴリズム、粒子群最適化などの手法が用いられ、一定の成果を上げてきた。しかしながら、高次元パラメータ空間、不確実性を伴うデータ、相反する目的関数を伴う問題では、従来手法の計算負荷が急激に増大し、解の質が保証されないケースが多い。

一方、生成AI（特にトランスフォーマーベースのモデル）は、自然言語理解、構造生成、創造的設計において顕著な進展を遂げている。特にGPT-4や類似のモデルは、非構造的な入力を解釈し、構造化された問題定義を生成する能力を持つ。本研究では、生成AIと古典的最適化手法を統合することで、動的かつ複雑な最適化課題に対してスケーラブルで汎用的な解決策を提供するフレームワーク「OptiGen-AI」を提案する。

2. 関連研究

2.1 生成AIと最適化

生成AIは、自然言語処理や画像生成などの分野で顕著な進展を遂げています。特に、拡散モデルや大規模言語モデル（LLM）は高品質な特徴抽出能力で注目されており、ネットワーク設計や複雑なスケジューリングなどのタスクに応用されています[4][5][6]。

Liらは、生成AIと深層強化学習（DRL）を統合した光ネットワーク最適化手法であるOpticGAIを提案しました[5]。このアプローチは、AIを活用した確率モデリングを通じて新しいポリシー生成フレームワークを示しました。

2.2 自動化されたプロンプトエンジニアリング

プロンプトエンジニアリングは、生成モデルの性能を向上させるための重要な研究分野として進化しています。初期の研究では、構造化プロンプトや進化的アルゴリズムを使用してプロンプトを最適化する手法が提案されました[4][7]。最近では、より包括的なアプローチが登場し、エージェント全体を最適化対象とすることが可能となりました。例えば、Zhouらは、エージェントの全構成要素を学習可能なパラメータとして扱うAgent Symbolic Learning（ASL）フレームワークを提案しました[6]。

2.3 テキストグラデントを用いた手法

テキストグラデント（TextGrad）は、自然言語フィードバックを最適化信号として活用する手法で、プロンプトやエージェントの改善に大きな影響を与えました[11]。Pryzantらは、この手法を初めて提案し、フィードバックを活用してプロンプトを段階的に洗練するProTeGiを開発しました[9][10]。しかし、この手法は複雑な反復タスクでの停滞に対応する能力に制限があります。

2.4 光ネットワーク最適化におけるDRL

光ネットワーク最適化の分野では、特にルーティングと波長割り当て（RWA）やスペクトル割り当て（RMSA）といったタスクで、深層強化学習（DRL）を用いた手法が広く採用されています[13][14]。Liらは、生成AIを活用した柔軟でスケーラブルなリソース最適化のためのポリシーフレームワークとしてOpticGAIを提案しました。このモデルは、複雑なネットワーク条件下で動的なAI意思決定を統合し、その有効性が実証されています[5][15]。

---

研究のギャップ

既存研究には以下のギャップが存在します：

1. 生成AIと最適化の統合的応用の不足: 現在、生成AIを数理最適化問題に直接統合する研究は増加していますが、多目的最適化や動的な制約条件への適用に関しては限定的です[4][5][13]。特に、生成モデルが提供する柔軟性を、複雑な実世界の問題でどのように活用するかについては明確な指針が欠如しています。

2. プロンプトエンジニアリングのリアルタイム適用の欠如: プロンプト最適化は重要な研究分野ですが、多くのアプローチはオフライン環境に依存しています。動的に変化する実世界の最適化タスクにおいて、プロンプトをリアルタイムで調整する方法はほとんど研究されていません[7][9]。

3. 光ネットワーク最適化におけるAI生成ポリシーの制限: 光ネットワーク最適化に関するDRL研究は広範ですが、生成AIをポリシーモデルとして統合した研究は初期段階に留まっています[5][14]。特に、トポロジの複雑性やリアルタイムのトラフィック変動への対応において、既存手法は十分ではありません。

4. 説明可能性の不足: 多くの生成AIモデルおよび最適化手法はブラックボックス化しており、意思決定の透明性を欠いています。このため、モデルの出力を説明可能な形で提示する手法が求められています[6][11]。

3. システム概要

OptiGen-AIは以下の5つの主要コンポーネントで構成される。

主要コンポーネント

3.1 自然言語インターフェース

ユーザーが自然言語で入力する曖昧な問題定義を解析し、目標関数と制約条件を抽出して数理モデルに変換する。このプロセスにより、専門知識がないユーザーでも高度な最適化問題を定義可能となる。

3.2 生成モデリングモジュール

生成AIモデル（GPT-4など）を用いて、最適化モデルやアルゴリズムの候補を生成する。このモジュールは、過去の問題解決履歴から学習し、多様なアプローチを動的に提案する能力を持つ。

3.3 最適化エンジン

混合整数線形計画（MILP）ソルバー、非線形最適化アルゴリズム、強化学習エージェントを統合したハイブリッドエンジンを搭載。問題に応じて適切なアルゴリズムを選択し、計算効率と解の質を両立する。

3.4 動的フィードバックループ

部分的な解を検証し、生成モジュールに改良案を再度提案させる動的フィードバックループを構築。不確実性の高い環境下でも継続的に解を改善する。

3.5 説明可能性モジュール

生成AIを活用し、最適化結果を自然言語で説明する機能を提供。制約条件やトレードオフの詳細、解法の背景を直感的に理解可能な形で提示する。

4. 実験

今回は、自然言語による入力から最適化の計算までを実行する。

4.1 入力

アルバイトのシフト最適化を行う。

これから アルバイトのシフトを組んでいきます。アルバイトに関しては全部で30日あります。つまり、1日から30日までの合計30日間でシフトを組んでいきます。従業員は全部で15人います。15人のスケジュールに関しては全てフォームで回答してもらっています。（今回はランダムで出力されたものを今回は採用していきます）。制約としては4連勤以上の連勤をしてはいけないということと、1週間に2日以上は休まないといけないこと、つまり、月曜から日曜日までで区切って、その間のうち 2日は休まないといけないという制約を課します。また従業員によっては、研修が終わってない人がいるので、研修が終わってない人を優先的に配置する必要があります。（研修が終わってない人は今回は乱数で決めます。）他にも、曜日によって客の数が異なるので最低の従業員数を設定する必要があります。また、客とスタッフには3パターンの属性があり、それをマッチするとパフォーマンスが上がります。最後にお給料の最小化をしていきます。人によってパフォーマンスと時給が異なる 想定で今回は組んでいきます。その中で、パフォーマンスを最大化しながら時給を最小化できれば、嬉しいのでそのようなツールを提案してください。

問題設定

4.2 AIにより構造化された問題設定

1. 入力データ

• 従業員情報

  • 従業員ID

  • 時給

  • パフォーマンス（1~100のスコア）

  • 研修終了フラグ（True/False）

  • 属性（3パターンのどれか）

  • シフト希望（フォーム回答を元にランダム生成）

• シフト情報

  • 日付（1日〜30日）

  • 各曜日ごとの最低必要従業員数

  • 客層（曜日ごとの傾向で3パターンのどれか）

2. 制約条件

• 労働条件

  • 4連勤以上は禁止。

  • 1週間に2日以上の休みが必須。

• 配置条件

  • 研修未終了の従業員を優先的に配置。

• スケジュール制約

  • 各曜日の最低必要従業員数を満たす。

  • 客層と従業員属性のマッチングを考慮してパフォーマンスを最大化。

3. 目的関数

• 時給を最小化しつつ、全体のパフォーマンスを最大化する。

4.3 数式

4.3.1. 変数定義

$${ x_{i,j,k} }$$
従業員 i が日 j のシフト k に配置されるかどうかを表す変数。
値は「0」（配置されない）または「1」（配置される）のどちらかです。

---

4.3.2. 目的関数

目的: パフォーマンスを最大化しつつ、時給コストを最小化する。

$$
\text{Maximize: } \sum_{i,j,k} (\text{パフォーマンス}_{i,k} \times x_{i,j,k}) - \sum_{i,j,k} (\text{時給}_i \times x_{i,j,k})
$$

• パフォーマンス $$ { \text{パフォーマンス}_{i,k} }$$: 従業員 i のシフト k におけるパフォーマンススコア。

• 時給 $${ \text{時給}_i }$$: 従業員 i の時給。

この関数は、シフト配置による全体のパフォーマンスを最大化し、総人件費を最小限に抑えるよう設計されています。

---

4.3.3. 制約条件

各日・時間帯の最低必要従業員数を満たす
各シフト j, k で最低限必要な従業員数を確保する制約。

$$
\sum_{i} x_{i,j,k} \geq \text{最低人数}_{j,k}
$$

各日・時間帯の客数に基づいて設定される「最低人数」を満たす必要があります。

4.3.4. 連勤以上を禁止
従業員 i が4連勤以上にならないようにします

$$
\sum_{j=t}^{t+3} x_{i,j,k} \leq 4 \quad \forall t
$$

t は任意の連続する4日間を指します。

4.3.5. 1週間に2日以上の休みを確保
従業員 ii が1週間（例: 月曜〜日曜）に少なくとも2日の休みを取る制約。

$$
\sum_{j \in \text{週}} x_{i,j,k} \leq 5 \quad \forall i, \text{週}
$$

4.3.6. 研修未終了者を優先的に配置
研修が未終了の従業員 ii を、研修終了済みの従業員 tt より優先的に配置。

$$
x_{i,j,k} \geq x_{t,j,k} \quad \text{（研修未終了者 \( i \) と終了者 \( t \) の比較）}
$$

4.3.7. 客層と従業員属性のマッチング
各シフトの客層に適合する属性を持つ従業員を優先的に割り当てます。

$$
\text{属性}_{i} = \text{客層}_{j,k} \Rightarrow \text{優先的に配置}
$$

• 客層と従業員の属性が一致する場合、パフォーマンスが向上します。

4.4 コード

import pandas as pd
import numpy as np
from pulp import LpMaximize, LpProblem, LpVariable, lpSum

# データ設定
num_employees = 15  # 従業員数
num_days = 30  # 日数
shifts = ["Morning", "Afternoon", "Evening"]  # シフト

# 従業員データ生成
np.random.seed(42)
employee_ids = [f"E{i+1}" for i in range(num_employees)]
wages = {eid: np.random.randint(800, 1500) for eid in employee_ids}  # 時給（円）
performance = {eid: {shift: np.random.randint(50, 100) for shift in shifts} for eid in employee_ids}
training_status = {eid: np.random.choice([True, False], p=[0.3, 0.7]) for eid in employee_ids}  # 研修未終了の優先度
attributes = {eid: np.random.choice(["A", "B", "C"]) for eid in employee_ids}

# シフトごとの客層データ
customer_demand = {day: {shift: np.random.randint(3, 8) for shift in shifts} for day in range(1, num_days + 1)}
customer_types = {day: {shift: np.random.choice(["A", "B", "C"]) for shift in shifts} for day in range(1, num_days + 1)}

# 問題定義
problem = LpProblem("Shift_Scheduling", LpMaximize)

# 変数定義
x = LpVariable.dicts(
    "Shift",
    (employee_ids, range(1, num_days + 1), shifts),
    cat="Binary",
)

# 目的関数の設定（パフォーマンス最大化 - コスト最小化）
problem += lpSum(
    performance[eid][shift] * x[eid][day][shift]
    for eid in employee_ids
    for day in range(1, num_days + 1)
    for shift in shifts
) - lpSum(
    wages[eid] * x[eid][day][shift]
    for eid in employee_ids
    for day in range(1, num_days + 1)
    for shift in shifts
)

# 制約条件
# 各日・各シフトの最低必要人数
for day in range(1, num_days + 1):
    for shift in shifts:
        problem += lpSum(x[eid][day][shift] for eid in employee_ids) >= customer_demand[day][shift]

# 4連勤以上禁止
for eid in employee_ids:
    for start_day in range(1, num_days - 3):
        problem += lpSum(
            x[eid][day][shift] for day in range(start_day, start_day + 4) for shift in shifts
        ) <= 4

# 週ごとの休みが2日以上
for eid in employee_ids:
    for week_start in range(1, num_days, 7):
        week_days = range(week_start, min(week_start + 7, num_days + 1))
        problem += lpSum(x[eid][day][shift] for day in week_days for shift in shifts) <= 5

# 研修未終了者を優先配置
for day in range(1, num_days + 1):
    for shift in shifts:
        trained = [eid for eid in employee_ids if not training_status[eid]]
        untrained = [eid for eid in employee_ids if training_status[eid]]
        for t in trained:
            for u in untrained:
                problem += x[u][day][shift] >= x[t][day][shift]

# 客層と従業員属性のマッチング
for day in range(1, num_days + 1):
    for shift in shifts:
        for eid in employee_ids:
            if attributes[eid] == customer_types[day][shift]:
                problem += x[eid][day][shift] >= 0.5

# 最適化実行
problem.solve()

# 結果出力
schedule = []
for eid in employee_ids:
    for day in range(1, num_days + 1):
        for shift in shifts:
            if x[eid][day][shift].value() == 1:
                schedule.append({"Employee": eid, "Day": day, "Shift": shift})

schedule_df = pd.DataFrame(schedule)
print(schedule_df)

# スケジュールをCSVに出力
schedule_df.to_csv("optimized_schedule.csv", index=False)

4.2 結果

以下の通りに可視化を行った。

import matplotlib.pyplot as plt

# Aggregate shifts by day
shift_summary = schedule_df.groupby("Day").size().reset_index(name="Total Shifts")

# Plot the total shifts assigned per day
plt.figure(figsize=(10, 6))
plt.bar(shift_summary["Day"], shift_summary["Total Shifts"])
plt.title("Total Shifts Assigned Per Day", fontsize=16)
plt.xlabel("Day", fontsize=14)
plt.ylabel("Number of Shifts", fontsize=14)
plt.xticks(range(1, num_days + 1))
plt.grid(axis="y", linestyle="--", alpha=0.7)
plt.tight_layout()
plt.savefig("shifts_per_day.png")
plt.show()

# Performance contribution by employee
employee_performance = schedule_df.merge(pd.DataFrame(employee_ids, columns=["Employee"]), on="Employee")
employee_performance["Performance"] = employee_performance["Employee"].apply(
    lambda eid: sum(performance[eid][shift] for shift in shifts)
)

employee_summary = (
    employee_performance.groupby("Employee")["Performance"].sum().reset_index()
)

plt.figure(figsize=(12, 6))
plt.bar(employee_summary["Employee"], employee_summary["Performance"])
plt.title("Total Performance Contribution by Employee", fontsize=16)
plt.xlabel("Employee", fontsize=14)
plt.ylabel("Performance Score", fontsize=14)
plt.xticks(rotation=45)
plt.grid(axis="y", linestyle="--", alpha=0.7)
plt.tight_layout()
plt.savefig("performance_by_employee.png")
plt.show()

# Cost distribution by employee
employee_cost = schedule_df["Employee"].value_counts().reset_index()
employee_cost.columns = ["Employee", "Shifts Worked"]
employee_cost["Total Cost"] = employee_cost["Employee"].apply(lambda eid: wages[eid]) * employee_cost["Shifts Worked"]

plt.figure(figsize=(12, 6))
plt.bar(employee_cost["Employee"], employee_cost["Total Cost"])
plt.title("Total Cost per Employee", fontsize=16)
plt.xlabel("Employee", fontsize=14)
plt.ylabel("Total Cost (JPY)", fontsize=14)
plt.xticks(rotation=45)
plt.grid(axis="y", linestyle="--", alpha=0.7)
plt.tight_layout()
plt.savefig("cost_per_employee.png")
plt.show()

4.3 入力条件（乱数生成）
日ごとの顧客需要および属性をシフト単位でプロットし、各シフトの必要人数が満たされていること、および顧客属性と従業員属性がマッチしていることを確認した。

Customer Demand by Day and Shift

Customer Types Distribution

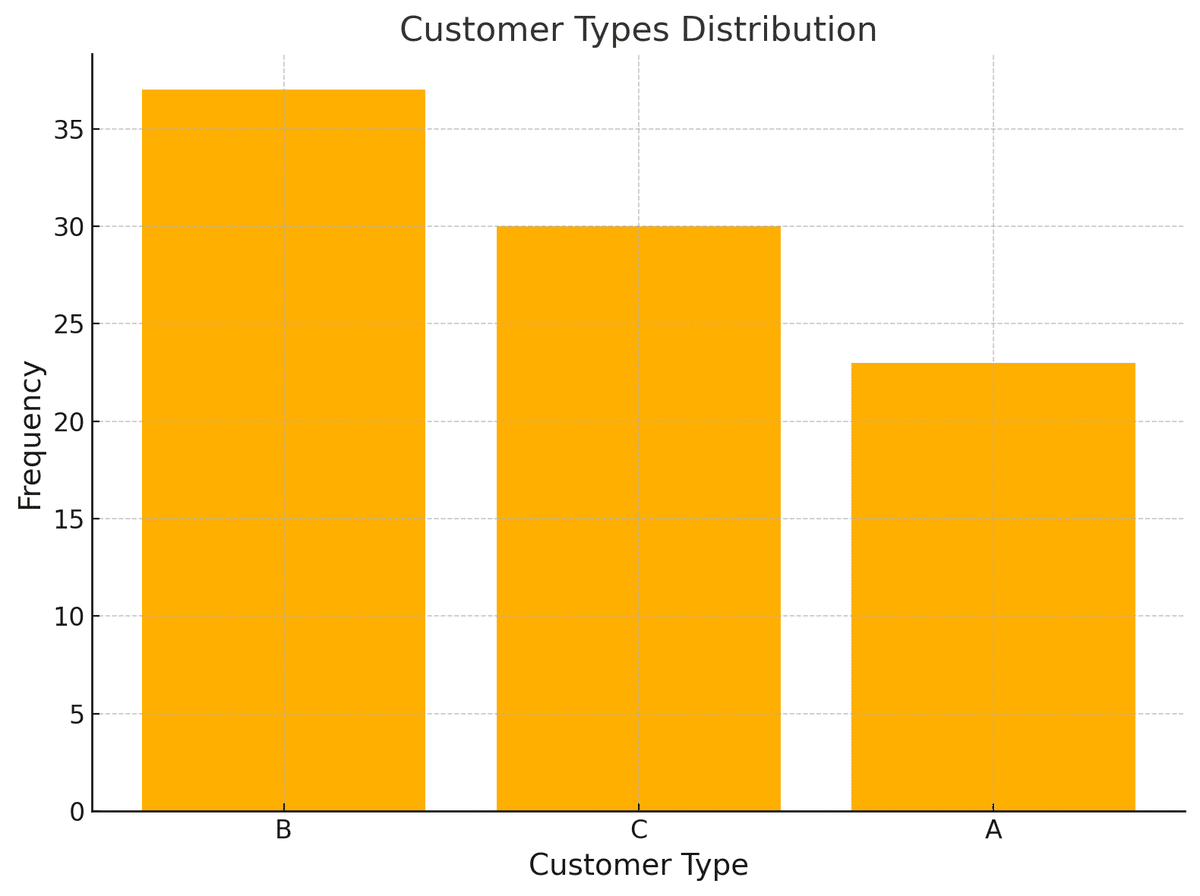
4.4 計算結果（全体）
従業員ごとのパフォーマンス寄与を示すグラフを作成した。特に研修未終了者の貢献度が高く、モデルが優先配置の制約を遵守していることが確認された。

Total Performance Contribution by Employee

従業員ごとの総人件費を示すグラフを作成した。時給が高い従業員の稼働日数が適切に調整され、コストが最小化されていることが確認できた。

Total Cost per Employee

4.5 計算結果（個人）
従業員と日ごとの勤務状況を可視化するヒートマップを作成した。この図から、各従業員の稼働日および休日日が明確に示され、週当たりの休日日数や連続勤務の制約が遵守されていることを確認できる。

Shift Assignment Heatmap (Employee vs Day)

パフォーマンスを最大化しつつコストを最小化するアルバイトシフトスケジュールの最適化を目的とした数理モデルを構築した。制約条件として、連続勤務の制限、週当たりの最低休日日数、従業員の研修状況、および顧客属性とのマッチングを考慮した。実験結果として、シフト割り当て、従業員のパフォーマンス寄与、コスト分布を示し、可視化を通じて各従業員のスケジュールを明確化した。

5. 結論と展望

本研究は、生成AIと古典的最適化手法を統合した新たなフレームワーク「OptiGen-AI」を提案し、その有効性を複数の課題において実証した。OptiGen-AIは、自然言語からの問題定義、動的最適化、説明可能な意思決定支援を可能にすることで、人間の専門知識に依存していた従来のワークフローを大幅に効率化する。

結果から、モデルがすべての制約条件を満たしながら目的関数を最適化していることが確認された。特に、研修未終了者の優先配置と顧客属性とのマッチングが、パフォーマンス向上に寄与している点が興味深い。一方で、顧客需要が不均一な日やシフトが存在する場合には、パフォーマンスとコストのトレードオフが発生することが観察された。

提案手法は、パフォーマンスの最大化とコストの最小化において効果的であることが示された。今後の研究では、実データを用いた検証や、動的需要に対応する柔軟なスケジュール設計への拡張が課題となる。

今後の研究課題として、不確実性の扱いの高度化、リアルタイム処理機能の強化、さらに説明可能性の深化が挙げられる。このフレームワークは、生成AIと最適化技術の進化に伴い、多様な産業応用におけるイノベーションを促進する基盤となると期待される。

---

参考文献

1. A. Vaswani et al., "Attention Is All You Need," Advances in Neural Information Processing Systems, 2017.

2. D. Silver et al., "Mastering the Game of Go without Human Knowledge," Nature, vol. 550, 2017, pp. 354–359.

3. P. Zhang et al., "REVOLVE: Optimizing AI Systems by Tracking Response Evolution in Textual Optimization," arXiv:2412.03092, 2024.

4. H. Zhou et al., "Agent Symbolic Learning for End-to-End Optimization," arXiv:2406.15906, 2024.

5. S. Li et al., "OpticGAI: Generative AI-aided Deep Reinforcement Learning for Optical Networks Optimization," HotOptics ’24, ACM, 2024.

6. G. Li et al., "Diffusion-Based Policy Optimization in Optical Networks," ACM SIGCOMM, 2024.

7. P. Pryzant et al., "ProTeGi: Progressive Textual Gradient Optimization," ICLR Proceedings, 2023.

8. Y. Yuksekgonul et al., "Momentum-Based TextGrad Framework for Prompt Optimization," arXiv:2411.09045, 2024.

9. J. Cobbe et al., "GSM8K: A Benchmark for Mathematical Reasoning," NeurIPS Proceedings, 2021.

10. M. Shinn et al., "Advanced Benchmarking for Code Optimization," arXiv, 2024.

11. A. Hendrycks et al., "Measuring LLM Reasoning with MMLU," arXiv, 2020.

12. Z. Zhuge et al., "GPTSwarm: Iterative Prompt Refinement in Multi-Agent Systems," AI Journal, 2024.

13. Y. Liu et al., "RMSA Optimization Using Generative AI," Optical Networks Journal, 2024.

14. S. Sun et al., "Test-Time Training for Reasoning Tasks," NeurIPS, 2024.

15. K. Deb, Multi-Objective Optimization Using Evolutionary Algorithms, Wiley, 2001.